
- •Линии второго порядка Лекция 14 Эллипс. Гипербола. Парабола
- •§ 28. Эллипс
- •Свойства эллипса
- •Задания для самостоятельной работы
- •§ 29. Гипербола
- •Свойства гиперболы
- •Задания для самостоятельной работы
- •§ 30. Парабола
- •Свойства параболы
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •§ 32. Приведение общего уравнения линии второго порядка к каноническому виду
- •Задания для самостоятельной работы
Задания для самостоятельной работы
1. Приведите уравнение эллипса к каноническому виду:
-
а)
 ;
;в)
 ;
;б)
 ;
;г)
 .
.
2. Дано каноническое
уравнение эллипса. Найдите большую и
малую «полуоси», координаты вершин,
координаты фокусов, фокальное расстояние,
фокальные радиусы точки
![]() ,
эксцентриситет, уравнения директрис:
,
эксцентриситет, уравнения директрис:
-
а)
 ;
;б)
 .
.
3. Постройте изображение эллипса, его фокусов и директрис:
-
а)
 ;
;б)
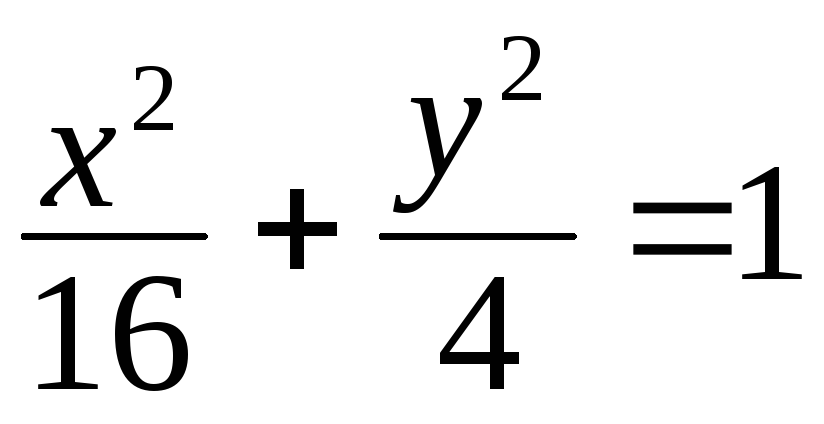 .
.
§ 29. Гипербола
Гиперболой
называется множество всех точек
плоскости, абсолютное значение разности
расстояний каждой из которых до данных
точек
![]() и
и![]() равно длине данного отрезка
равно длине данного отрезка![]() ,
где
,
где![]() .
.
Коротко можно
записать определение гиперболы
![]() так:
так:
![]() .
(39)
.
(39)
Точки
![]() и
и![]() называютсяфокусами
гиперболы, а расстояние между ними -
фокальным
расстоянием.
называютсяфокусами
гиперболы, а расстояние между ними -
фокальным
расстоянием.
Если
![]()
точка данной гиперболы, то отрезки
точка данной гиперболы, то отрезки
![]() и
и![]() (а также их длины) называютсяфокальными
радиусами точки
(а также их длины) называютсяфокальными
радиусами точки
![]() .
.
П усть
на плоскости даны две различные точки
усть
на плоскости даны две различные точки![]() и
и![]() .
Обозначим через
.
Обозначим через![]() середину отрезка
середину отрезка![]() .
Рассмотрим прямоугольную декартову
систему координат
.
Рассмотрим прямоугольную декартову
систему координат![]() ,
где
,
где![]() (рис. 90).
(рис. 90).
Выведем уравнение
гиперболы
![]() с фокусами
с фокусами![]() и
и![]() в системе координат
в системе координат![]() .
.
Пусть
![]() .
.
Замечание.
Так как
![]() ,
то для гиперболы всегда
,
то для гиперболы всегда![]() ,
т.е.
,
т.е.
![]() .
.
Пусть
![]() .
Так как
.
Так как![]() в
в![]() ,
то
,
то
![]() .
.
По определению
гиперболы
![]() .
Преобразуем это уравнение:
.
Преобразуем это уравнение:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Возведем обе части последнего уравнения в квадрат:
![]() ;
;
![]() ;
;
![]() .
.
Разделим обе части
этого уравнения на
![]() :
:
![]() .
.
Так как для гиперболы
![]() ,
то
,
то![]() .
Положим
.
Положим![]() .
Тогда
.
Тогда
![]() ,
где
,
где
![]() .
(40)
.
(40)
Итак, доказано,
что если
![]() ,
то координаты точки
,
то координаты точки![]() удовлетворяют уравнению (40).
удовлетворяют уравнению (40).
Докажем, что если
координаты точки
![]() удовлетворяют уравнению (40), то она
принадлежит гиперболе
удовлетворяют уравнению (40), то она
принадлежит гиперболе![]() .
.
Пусть ![]() ,
где
,
где ![]() ,
,
![]()
координаты точки
координаты точки
![]() .
.
Найдем
![]() .
Выразим
.
Выразим![]() из уравнения
из уравнения![]() :
:
![]() .
.
Найдем

![]() .
.
Аналогично
![]() .
.
при
при

Тогда
![]() .
.
Из условия (39)
следует, что
![]() .
.
Итак, уравнение (40) есть уравнение гиперболы. Оно называется каноническим уравнением гиперболы.
Пользуясь каноническим уравнением гиперболы, докажем геометрические свойства гиперболы, которые понадобятся для построения изображения гиперболы.
Свойства гиперболы

1.
Из уравнения (40) следует, что
![]() или
или![]() .
Следовательно, все точки гиперболы
лежат вне полосы, ограниченной прямыми
.
Следовательно, все точки гиперболы
лежат вне полосы, ограниченной прямыми![]() и
и![]() (рис.
91).
(рис.
91).
2. Симметрия относительно начала координат и осей координат.
Пусть
![]()
![]() и
и
![]() .
Из первого тождества следует, что
.
Из первого тождества следует, что![]() ,
из второго – что
,
из второго – что![]() ,
из третьего – что
,
из третьего – что![]() ,
а это означает, что гипербола
,
а это означает, что гипербола![]() симметрична относительно начала
координат, оси
симметрична относительно начала
координат, оси![]() и оси
и оси![]() соответственно. Таким образом, точка
соответственно. Таким образом, точка![]() являетсяцентром
симметрии,
оси
являетсяцентром
симметрии,
оси
![]() и
и![]()
осями симметрии
гиперболы
осями симметрии
гиперболы
![]() .
.
Прямая, проходящая через фокусы, называется действительной осью симметрии, а перпендикулярная к ней ось – мнимой осью симметрии гиперболы.
3. Точки пересечения гиперболы с осями симметрии.
![]()
Чтобы найти точки
пересечения гиперболы
![]() с осью
с осью![]() ,
надо решить систему их уравнений:
,
надо решить систему их уравнений:
Решая систему,
получаем:
![]() .
.
Аналогично находим,
что
![]() .
.
Точки пересечения гиперболы со своими осями симметрии называются вершинами гиперболы. Таким образом, гипербола имеет две вершины.
Отрезки
![]() и
и![]() называются соответственнодействительной
и мнимой
«осями» гиперболы,
а положительные числа
называются соответственнодействительной
и мнимой
«осями» гиперболы,
а положительные числа
![]() и
и![]()
действительной
и мнимой
«полуосями» гиперболы.
действительной
и мнимой
«полуосями» гиперболы.
4.
Найдем точки пересечения гиперболы с
прямой
![]() .
.
Для этого решим
систему

Получаем уравнение
![]() .
Корни
.
Корни![]()
это абсциссы точки пересечения прямой
это абсциссы точки пересечения прямой
![]() с
с![]() .
Рассмотрим три случая:
.
Рассмотрим три случая:
Если
 ,
т.е.
,
т.е. ,
то
,
то и
и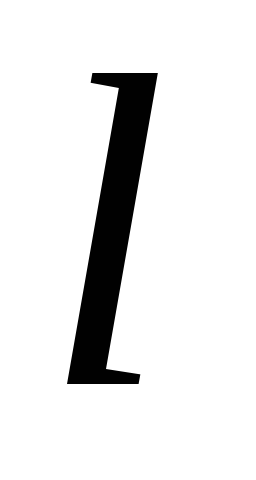 имеют две общие точки;
имеют две общие точки;Если
 ,
т.е.
,
т.е.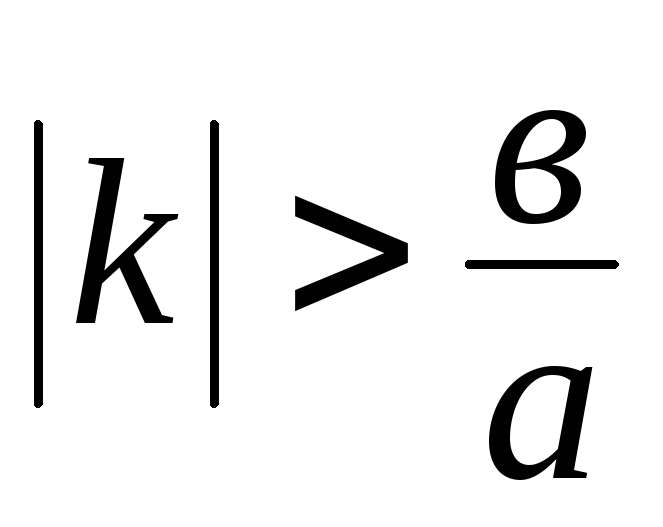 ,
то
,
то ;
;Е
 сли
сли ,
т.е.
,
т.е. ,
то
,
то .
.
Следовательно, все точки гиперболы расположены в заштрихованных областях (рис. 92). Гипербола имеет две ветви.
Случаю 3) соответствуют
две прямые
![]() и
и![]() с угловыми коэффи-
с угловыми коэффи-
циентами
![]() и
и![]() .
Эти прямые (
.
Эти прямые (![]() и
и![]() )
называютсяасимптотами
гиперболы.
)
называютсяасимптотами
гиперболы.
При неограниченном
возрастании абсолютной величины абсциссы
точки
![]() гиперболы точка
гиперболы точка![]() неограниченно приближается к асимптоте.
неограниченно приближается к асимптоте.
У читывая
свойства 1-
4,
построим изображение гиперболы (рис.
93):
читывая
свойства 1-
4,
построим изображение гиперболы (рис.
93):
Число
![]() называетсяэксцентриситетом
гиперболы. Так как для гиперболы
называетсяэксцентриситетом
гиперболы. Так как для гиперболы
![]() ,
то
,
то![]() .
Чем больше
.
Чем больше![]() ,
тем больше гипербола «вытянута» вдоль
мнимой оси.
,
тем больше гипербола «вытянута» вдоль
мнимой оси.
Гипербола, у которой
![]() ,
называетсяравносторонней.
Ее каноническое уравнение
,
называетсяравносторонней.
Ее каноническое уравнение
![]() .
Уравнения ее асимптот
.
Уравнения ее асимптот![]() .
.
Директрисами
эллипса называются две прямые, параллельные
мнимой оси и отстоящие от нее на расстоянии
![]() .
.
Уравнения директрис:
![]() или
или
![]() ;
;
![]() или
или
![]() (рис. 94).
(рис. 94).
Гипербола обладает
следующим директориальным
свойством:
для любой точки
![]() ,
принадлежащей гиперболе, отношение
расстояния от
,
принадлежащей гиперболе, отношение
расстояния от![]() до фокуса к расстоянию от
до фокуса к расстоянию от![]() до соответствующей директрисы равно
эксцентриситету, т.е.
до соответствующей директрисы равно
эксцентриситету, т.е.
 (рис. 94).
(рис. 94).

Замечание 1. Директрисы гиперболы не имеют общих точек с гиперболой.
Гипербола
![]() называетсясопряженной
к гиперболе
называетсясопряженной
к гиперболе
![]() .
Ее мнимой осью является ось
.
Ее мнимой осью является ось![]() (на рис. 94 она изображена пунктиром).
(на рис. 94 она изображена пунктиром).
