lect3

Ларин Александр Александрович “Курс высшей математики. Часть 3.”

Признак Даламбера.

(Жан Лерон Даламбер (1717 – 1783) – французский математик)

Если для ряда ∑un с положительными членами существует такое число q<1, что для всех достаточно больших n выполняется неравенство

un+1 ≤ q, un

то ряд ∑un сходится, если же для всех достаточно больших n выполняется условие

un+1 ≥1, un

то ряд ∑un расходится.

Предельный признак Даламбера.

Предельный признак Даламбера является следствием из приведенного выше признака Даламбера.

Если существует предел lim un+1 = ρ, то при ρ < 1 ряд сходится, а при ρ > 1 –

n→∞ un

расходится. Если ρ = 1, то на вопрос о сходимости ответить нельзя.

∞

n

Пример. Определить сходимость ряда ∑

.

n

n=1

2

1

n

n +1

un+1

(n +1)2n

n +1

1+

1

un =

;

un+1 =

;

lim

= lim

=

=

n

=

<1

2n

2n+1

un

2n+1 n

2n

2

2

n→∞

n→∞

Вывод: ряд сходится.

Пример. Определить сходимость ряда 1+ 11! + 21! +... + n1! +...

un =

1

;

un+1 =

1

; lim

un+1

= lim

n!

= lim

1

= 0 <1

n!

(n +1)!

(n +1)!

n→∞ un

n→∞

n→∞ n +1

Вывод: ряд сходится.

Признак Коши. (радикальный признак)

Если для ряда ∑un с неотрицательными членами существует такое число q<1, что для всех достаточно больших n выполняется неравенство

n un ≤ q ,

то ряд ∑un сходится, если же для всех достаточно больших n выполняется неравенство

n un ≥1,

71

Ларин Александр Александрович “Курс высшей математики. Часть 3.”

то ряд ∑un расходится.

Следствие. Если существует предел lim n un = ρ, то при ρ<1 ряд сходится, а при

n→∞

ρ>1 ряд расходится.

∞

2n

2

+1

n

2

Пример. Определить сходимость ряда ∑

3n

+ 5

.

n=1

1

2n2 +1

2 +

2

lim n un

= lim

= lim

n2

=

<1

3n2 + 5

3

n→∞

n→∞

n→∞

5

3 +

n2

Вывод: ряд сходится.

∞

1 n

Пример. Определить сходимость ряда ∑ 1+

.

n=1

n

1

lim n

un = lim 1+

=1.

n→∞

n→∞

n

Т.е. признак Коши не дает ответа на вопрос о сходимости ряда. Проверим выполнение необходимых условий сходимости. Как было сказано выше, если ряд сходится, то общий член ряда стремится к нулю.

					1	n
	lim u	n	= lim 1	+			= e ≠ 0 ,
					n
	n→∞		n→∞

таким образом, необходимое условие сходимости не выполняется, значит, ряд расходится.

Интегральный признак Коши.

Если ϕ(х) – непрерывная положительная функция, убывающая на промежутке

∞	∞
[1;∞), то ряд ϕ(1) + ϕ(2) + …+ ϕ(n) + … = ∑ϕ(n) и несобственный интеграл ∫ϕ(x)dx
n=1	1

одинаковы в смысле сходимости.

Пример. Ряд 1+ 21α + 31α +... + n1α +... сходится при α>1 и расходится α≤1 т.к.

соответствующий несобственный интеграл ∞∫ dx сходится при α>1 и расходится α≤1.

α

1 x

		∞		1
Ряд ∑						называется общегармоническим рядом.
				α
	n=1			n
			Следствие. Если f(x) и ϕ(х)					– непрерывные функции на интервале (a, b] и
		f (x)				= h, h ≠ 0, то интегралы	b	b
lim								f (x)dx и ϕ(x)dx ведут себя одинаково в смысле
		ϕ(x)					a
x→a+0							∫	∫

сходимости.

72

Ларин Александр Александрович “Курс высшей математики. Часть 3.”

При использовании компьютерной версии “Курса высшей математики” возможно запустить программу, исследующую на сходимость числовые ряды по всем рассмотренным выше признакам. Достаточно ввести общий член ряда и нажать Enter. Все признаки будут проверяться по очереди.

Для запуска программы дважды щелкните на значке:

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (© Waterloo Maple Inc.) любой версии, начиная с Maple V Release 4.

Знакопеременные ряды.

Знакочередующиеся ряды.

Знакочередующийся ряд можно записать в виде:

u1 −u2 + u3 −u4 +... + (−1)n+1 un +...

где un > 0, n =1,2,3,...

Признак Лейбница.

Если у знакочередующегося ряда u1 −u2 + u3 −u4 +... + (−1)n+1 un +... абсолютные величины ui убывают u1 > u2 > u3 > ... и общий член стремится к нулю un → 0 , то ряд

сходится.

Абсолютная и условная сходимость рядов.

Рассмотрим некоторый знакопеременный ряд (с членами произвольных знаков).

∞

u1 +u2

+... +un

+... = ∑un

(1)

n=1

и ряд, составленный из абсолютных величин членов ряда (1):

∞

u1

+

u2

+... +

un

+... = ∑

un

(2)

n=1

Теорема. Из сходимости ряда (2) следует сходимость ряда (1).

Доказательство. Ряд (2) является рядом с неотрицательными членами. Если ряд

(2) сходится, то по критерию Коши для любого ε>0 существует число N, такое, что при

n>N и любом целом p>0 верно неравенство:

un+1

+

un+2

+... +

un+ p

< ε

По свойству абсолютных величин:

un+1 + un+2 +... + un+ p

≤

un+1

+

un+2

+... +

un+ p

< ε

un+1 + un+2

+... + un+ p

< ε

То есть по критерию Коши из сходимости ряда (2) следует сходимость ряда (1).

73

Ларин Александр Александрович “Курс высшей математики. Часть 3.”

Определение. Ряд ∑un называется абсолютно сходящимся, если сходится ряд

∑un .

Очевидно, что для знакопостоянных рядов понятия сходимости и абсолютной сходимости совпадают.

Определение. Ряд ∑un называется условно сходящимся, если он сходится, а ряд ∑un расходится.

Признаки Даламбера и Коши для знакопеременных рядов.

Пусть ∑un - знакопеременный ряд.

Признак Даламбера. Если существует предел lim un+1 = ρ, то при ρ<1 ряд

n→∞ un

∑un будет абсолютно сходящимся, а при ρ>1 ряд будет расходящимся. При ρ=1 признак не дает ответа о сходимости ряда.

Признак Коши. Если существует предел lim n		un		= ρ, то при ρ<1 ряд	∑un
n→∞

будет абсолютно сходящимся, а при ρ>1 ряд будет расходящимся. При ρ=1 признак не дает ответа о сходимости ряда.

Свойства абсолютно сходящихся рядов.

1) Теорема. Для абсолютной сходимости ряда ∑un необходимо и достаточно,

чтобы его можно было представить в виде разности двух сходящихся рядов с неотрицательными членами.

Следствие. Условно сходящийся ряд является разностью двух расходящихся рядов с неотрицательными стремящимися к нулю членами.

2)В сходящемся ряде любая группировка членов ряда, не изменяющая их порядка, сохраняет сходимость и величину ряда.

3)Если ряд сходится абсолютно, то ряд, полученный из него любой перестановкой членов, также абсолютно сходится и имеет ту же сумму.

Перестановкой членов условно сходящегося ряда можно получить условно сходящийся ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.

4) Теорема. При любой группировке членов абсолютно сходящегося ряда (при этом число групп может быть как конечным, так и бесконечным и число членов в группе может быть как конечным, так и бесконечным) получается сходящийся ряд, сумма которого равна сумме исходного ряда.

74

Ларин Александр Александрович “Курс высшей математики. Часть 3.”

	∞	∞
5) Если	ряды ∑un и	∑vn	сходятся	абсолютно	и их суммы	равны
	n=1	n=1
соответственно	S и σ, то	ряд,	составленный из всех		произведений	вида
ui vk , i, k =1,2,...	взятых в каком угодно порядке,			также сходится абсолютно и его

сумма равна Sσ - произведению сумм перемножаемых рядов.

Если же производить перемножение условно сходящихся рядов, то в результате можно получить расходящийся ряд.

Функциональные последовательности.

Определение. Если членами ряда будут не числа, а функции от х, то ряд называется функциональным.

Исследование на сходимость функциональных рядов сложнее исследования числовых рядов. Один и тот же функциональный ряд может при одних значениях переменной х сходиться, а при других – расходиться. Поэтому вопрос сходимости функциональных рядов сводится к определению тех значений переменной х, при которых ряд сходится.

Совокупность таких значений называется областью сходимости.

Так как пределом каждой функции, входящей в область сходимости ряда, является некоторое число, то пределом функциональной последовательности будет являться некоторая функция:

f (x) = lim fn (x)

n→∞

Определение. Последовательность {fn(x)} сходится к функции f(x) на отрезке [a,b], если для любого числа ε>0 и любой точки х из рассматриваемого отрезка существует номер N = N(ε, x), такой, что неравенство

f (x) − fn (x) < ε

выполняется при n>N.

При выбранном значении ε>0 каждой точке отрезка [a,b] соответствует свой номер и, следовательно, номеров, соответствующих всем точкам отрезка [a,b], будет бесчисленное множество. Если выбрать из всех этих номеров наибольший, то этот номер будет годиться для всех точек отрезка [a,b], т.е. будет общим для всех точек.

Определение. Последовательность {fn(x)} равномерно сходится к функции f(x) на отрезке [a,b], если для любого числа ε>0 существует номер N = N(ε), такой, что неравенство

f (x) − fn (x) < ε

выполняется при n>N для всех точек отрезка [a,b].
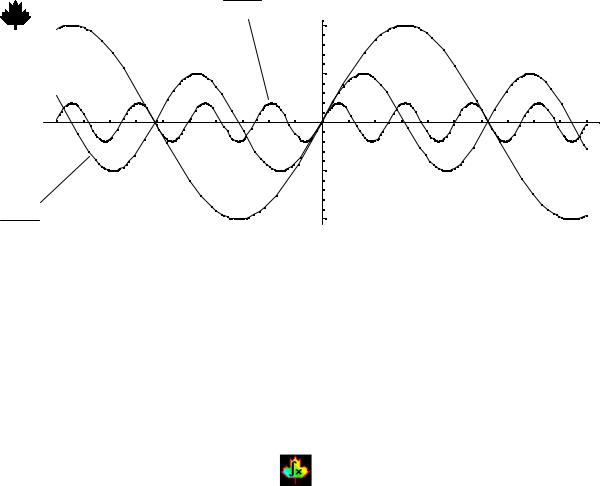
Пример. Рассмотрим последовательность	sin x	,	sin 2x	,...,	sin nx	,...
	1				n
		2

Данная последовательность сходится на всей числовой оси к функции f(x)=0, т.к.

	lim	sin nx	= 0, −∞ < x < ∞
		n
	n→0

Построим графики этой последовательности:

75

	Ларин Александр Александрович “Курс высшей математики. Часть 3.”
sinx		sin 5x
		5
		1
		0 . 5
- 4	- 2	2	4
		- 0 . 5
sin 2x		- 1
2
Как видно, при увеличении числа n график последовательности приближается к
оси х.

При использовании компьютерной версии “Курса высшей математики” возможно запустить программу, которая исследует на сходимость знакочередующиеся ряды и определяет характер сходимости. Достаточно ввести общий член ряда и множитель, определяющий знак и нажать Enter. Все рассмотренные выше признаки будут проверены по очереди.

Для запуска программы дважды щелкните на значке:

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (© Waterloo Maple Inc.) любой версии, начиная с Maple V Release 4.

Функциональные ряды.

Определение.	Частными (частичными) суммами	функционального ряда
∞	n
∑un (x) называются функции Sn (x) = ∑uk (x), n =1,2,...
n=1	k =1
	∞
Определение. Функциональный ряд ∑un (x) называется сходящимся в точке
(х=х0), если в этой	n=1
	точке сходится последовательность его	частных сумм. Предел

∞

последовательности {Sn (x0 )} называется суммой ряда ∑un (x) в точке х0.

n=1

76

Ларин Александр Александрович “Курс высшей математики. Часть 3.”

Определение. Совокупность всех значений х, для которых сходится ряд

∞

∑un (x) называется областью сходимости ряда.

n=1

∞

Определение. Ряд ∑un (x) называется равномерно сходящимся на отрезке

n=1

[a,b], если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.

Теорема. (Критерий Коши равномерной сходимости ряда)

∞

Для равномерной сходимости ряда ∑un (x) необходимо и достаточно, чтобы

n=1

для любого числа ε>0 существовал такой номер N(ε), что при n>N и любом целом p>0 неравенство

un+1 (x) +un+2 (x) +... +un+ p (x) < ε

выполнялось бы для всех х на отрезке [a,b].

Теорема. (Признак равномерной сходимости Вейерштрасса)

(Карл Теодор Вильгельм Вейерштрасс (1815 – 1897) – немецкий математик)

∞

Ряд ∑un (x) сходится равномерно и притом абсолютно на отрезке [a,b], если

n=1

модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами :

M1 + M 2 +... + M n +...

т.е. имеет место неравенство:

un (x) ≤ M n .

∞

Еще говорят, что в этом случае функциональный ряд ∑un (x) мажорируется

n=1

∞

числовым рядом ∑Μn .

n=1

∞

cos nx

Пример. Исследовать на сходимость ряд ∑

.

3

n=1

n

cos nx

cos nx

≤

1

.

Так как

≤1 всегда, то очевидно, что

n3

n3

1

∞

При этом известно, что общегармонический ряд

∑

при α=3>1 сходится, то в

α

n=1

n

соответствии с признаком Вейерштрасса исследуемый ряд равномерно сходится и притом в любом интервале.

Пример. Исследовать на сходимость ряд ∑∞ xn .

n=1 n3

77

Ларин Александр Александрович “Курс высшей математики. Часть 3.”

	На отрезке [-1,1] выполняется неравенство	xn	≤	1	т.е. по признаку Вейерштрасса на
		n3		n3

этом отрезке исследуемый ряд сходится, а на интервалах (- , -1) (1, ) расходится.

Свойства равномерно сходящихся рядов.

1) Теорема о непрерывности суммы ряда.

∞

Если члены ряда ∑un (x) - непрерывные на отрезке [a,b] функции и ряд

n=1

сходится равномерно, то и его сумма S(x) есть непрерывная функция на отрезке [a,b].

2) Теорема о почленном интегрировании ряда.

Равномерно сходящийся на отрезке [a,b] ряд с непрерывными членами можно почленно интегрировать на этом отрезке, т.е. ряд, составленный из интегралов от его членов по отрезку [a,b] , сходится к интегралу от суммы ряда по этому отрезку.

β ∞	∞ β
∫∑un (x)dx = ∑∫un (x)dx; α,β [a,b]
α n=1	n=1 α

3) Теорема о почленном дифференцировании ряда.

∞

Если члены ряда ∑un (x) сходящегося на отрезке [a,b] представляют собой

n=1

непрерывные функции, имеющие непрерывные производные, и ряд, составленный из

∞

этих производных ∑un′ (x) сходится на этом отрезке равномерно, то и данный ряд

n=1

сходится равномерно и его можно дифференцировать почленно.

	d	∞	∞	dun (x)
		∑un (x) = ∑
				dx
	dx n=1		n=1

На основе того, что сумма ряда является некоторой функцией от переменной х, можно производить операцию представления какой – либо функции в виде ряда (разложения функции в ряд), что имеет широкое применение при интегрировании, дифференцировании и других действиях с функциями.

На практике часто применяется разложение функций в степенной ряд.

При использовании компьютерной версии “Курса высшей математики” возможно запустить программу, которая определяет интервал сходимости для произвольного функционального ряда.

Для запуска программы дважды щелкните на значке

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (© Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.

78

Ларин Александр Александрович “Курс высшей математики. Часть 3.”

Степенные ряды.

Определение. Степенным рядом называется ряд вида

∞

a0 + a1 x + a2 x2 +... + an xn +... = ∑an xn .

n=0

Для исследования на сходимость степенных рядов удобно использовать признак Даламбера.

Пример. Исследовать на сходимость ряд x +

x2

x3

xn

+

+

... +

+...

2

3

n

Применяем признак Даламбера:

un+1

xn+1

xn

x

lim

= lim

n +

1

= lim

= lim

=

x

.

un

xn

n +1

1

n→∞

n→∞

n→∞

n→∞

1+

n

n

Получаем, что этот ряд сходится при

x

<1 и расходится при

x

>1.

Теперь определим сходимость в граничных точках 1 и –1.

При х = -1: −1+ 12 − 13 + 14 −... ряд сходится по признаку Лейбница (см. Признак Лейбница.).

При х = 1: 1+ 12 + 13 +... + 1n +... ряд расходится (гармонический ряд).

Теоремы Абеля.

(Нильс Хенрик Абель (1802 – 1829) – норвежский математик)

∞

Теорема. Если степенной ряд a0 + a1 x + a2 x2 +... + an xn +... = ∑an xn сходится

n=0

при x = x1 , то он сходится и притом абсолютно для всех x < x1 .

Доказательство. По условию теоремы, так как члены ряда ограничены, то an x1n ≤ k,

где k- некоторое постоянное число. Справедливо следующее неравенство:

a

n

xn

=

a

xn

x

n

≤ k

x

n

n 1

x

x

1

1

Из этого неравенства видно, что при x<x1 численные величины членов нашего ряда будут меньше ( во всяком случае не больше ) соответствующих членов ряда правой части записанного выше неравенства, которые образуют геометрическую

	прогрессию. Знаменатель этой прогрессии	x	по условию теоремы меньше единицы,
		x
		1

следовательно, эта прогрессия представляет собой сходящийся ряд.

Поэтому на основании признака сравнения делаем вывод, что ряд ∑an xn сходится, а значит ряд ∑an xn сходится абсолютно.

79

Ларин Александр Александрович “Курс высшей математики. Часть 3.”

Таким образом, если степенной ряд ∑an xn сходится в точке х1, то он абсолютно сходится в любой точке интервала длины 2 х1 с центром в точке х = 0.

Следствие. Если при х = х1 ряд расходится, то он расходится для всех x > x1 .

Таким образом, для каждого степенного ряда существует такое положительное число R, что при всех х таких, что x < R ряд абсолютно сходится, а при всех x > R ряд

расходится. При этом число R называется радиусом сходимости. Интервал (-R, R)

называется интервалом сходимости.

Отметим, что этот интервал может быть как замкнутым с одной или двух сторон, так и не замкнутым.

Радиус сходимости может быть найден по формуле:

R = lim an−1

n→∞ an

Пример. Найти область сходимости ряда x +

x2

+

x3

+... +

xn

+...

2!

3!

n!

1

an−1

n!

Находим радиус сходимости R = lim

= lim

(n −1)!

= lim

= lim

n

=

∞

.

an

1

(n −1)!

n→∞

n→∞

n→∞

n→∞

n!

Следовательно, данный ряд сходится при любом значении х. Общий член этого ряда стремится к нулю.

lim xn = 0.

n→∞ n!

Теорема. Если степенной ряд ∑an xn сходится для положительного значения х=х1 , то он сходится равномерно в любом промежутке внутри (− x1 ; x1 ) .

Действия со степенными рядами.

1) Интегрирование степенных рядов.

∞

Если некоторая функция f(x) определяется степенным рядом: f (x) = ∑an xn , то

n=0

интеграл от этой функции можно записать в виде ряда:

	∞	∞	∞	an
	∫ f (x)dx = ∫∑an xn dx = ∑∫an xn dx = ∑					xn+1 + C
				n +1
	n=0	n=0	n=0

2) Дифференцирование степенных рядов.

Производная функции, которая определяется степенным рядом, находится по формуле:

′	d	∞	n	∞	d		n	∞	n−1
f (x) =		∑an x		= ∑		(an x		)= ∑nan x
					dx
	dx n=0			n=0				n=0

80