
- •Глава 1. Действительные функции одного переменного
- •1.1. Основные понятия и определения
- •Задачи для самостоятельного решения
- •1.2. Некоторые типы функций
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •1.3. Обратная функция
- •Задачи для самостоятельного решения
- •Ответы к задачам главы 1:
- •Глава 2. Предел функции
- •2.1. Предел функции. Основные понятия
- •2.2. Предел дробно-рациональной функции. Иррациональные выражения.
- •Задачи для самостоятельного решения
- •2.3. Бесконечно малые величины. Первый замечательный предел.
- •Задачи для самостоятельного решения
- •2.4. Второй замечательный предел
- •Задачи для самостоятельного решения
- •Ответы к задачам главы 2:
- •Глава 3. Непрерывность функции
- •Задачи для самостоятельного решения
- •Ответы к задачам главы 3:
- •Глава4. Дифференциальное исчисление функции одной переменной
- •4.1. Производная. Дифференцирование явно заданных функций
- •Производная сложной функции. Пусть функция имеет производную в точке, а функцияимеет производную в точке. Тогда сложная функцияимеет производную в точкеи справедливо равенство;.
- •Задачи для самостоятельного решения
- •4.5. Дифференциал
- •Необходимым и достаточным условием дифференцируемости функции в точке является существование у функции производной в данной точке, при этом справедливо равенство .
- •Дифференциалом второго порядка функции называется первый дифференциал первого дифференциала, то естьи он обозначаетсяили.
- •Задачи для самостоятельного решения
- •4.8. Формула Тейлора
- •Задачи для самостоятельного решения
- •Ответы к задачам главы 4:
- •Глава 5. Исследование функций с помощью производных
- •5.1. Возрастание и убывание функций
- •5.2. Точки экстремума функций.
- •Задачи для самостоятельного решения
- •5.3. Исследование функций на выпуклость и вогнутость. Точки перегиба функций.
- •Задачи для самостоятельного решения
- •5.4. Асимптоты графика функции
- •Задачи для самостоятельного решения
- •5.5 Общая схема исследования функций.
- •Задачи для самостоятельного решения
- •Ответы к задачам главы 5:
Задачи для самостоятельного решения
55. В каких точках
угловой коэффициент касательной к
кубической параболе
![]() равен 3?
равен 3?
56. При каком значении
независимой переменной касательные к
кривым
![]() и
и![]() параллельны?
параллельны?
57. Составить уравнение
касательной и нормали к линии
![]() в точке с абсциссой
в точке с абсциссой![]() .
.
58. Составить уравнение
нормали к линии
![]() в
точке с абсциссой
в
точке с абсциссой![]() .
.
59. Найти угловой
коэффициент касательной к линии
![]() ,
,![]() в точке
в точке![]() .
.
60. Составить уравнение
касательной и нормали к линии
![]() ,
,![]() при
при![]() .
.
В следующих задачах найти углы, под которыми пересекаются линии.
61.
![]() и
и![]() .
62.
.
62.![]() и
и![]() .
.
63.
![]() и
и .
.
64. Сторона квадрата
увеличивается со скоростью
![]() .
Какова скорость изменения периметра и
площади квадрата в тот момент, когда
его сторона равна
.
Какова скорость изменения периметра и
площади квадрата в тот момент, когда
его сторона равна
![]() ?
?
4.5. Дифференциал
Функция
![]() называетсядифференцируемой
в точке
называетсядифференцируемой
в точке
![]() ,
если ее приращение
,
если ее приращение![]() в
этой точке может быть представлено в
виде
в
этой точке может быть представлено в
виде![]() ,
где
,
где![]() -
постоянная, не зависящая от
-
постоянная, не зависящая от![]() ,
а
,
а![]() - бесконечно малая величина при
- бесконечно малая величина при![]() .
.
Необходимым и достаточным условием дифференцируемости функции в точке является существование у функции производной в данной точке, при этом справедливо равенство .
Дифференциалом
функции
![]() в точке
в точке![]() называется главная линейная часть
приращения функции в точке
называется главная линейная часть
приращения функции в точке![]() и обозначается
и обозначается![]() .
.![]() .
.
Свойства
дифференциала. Пусть
![]() и
и![]() дифференцируемые функции. Тогда
справедливы равенства:
дифференцируемые функции. Тогда
справедливы равенства:
1.
![]() ,
с – постоянная. 2.
,
с – постоянная. 2.![]() .
.
3.
![]() .
4.
.
4.![]() ,
,![]()
5. Пусть
![]() сложная функция, образованная композицией
дифференцируемых функций
сложная функция, образованная композицией
дифференцируемых функций![]() и
и![]() .
Тогда
.
Тогда![]() .
Эти равенства выражаютсвойство
инвариантности формы первого дифференциала.
.
Эти равенства выражаютсвойство
инвариантности формы первого дифференциала.
Г еометрический
смысл дифференциала.
еометрический
смысл дифференциала.
Д
Рис 1 ![]()
![]() в точке
в точке![]() есть приращение ординаты касательной,
проведенной к графику функции в точке
есть приращение ординаты касательной,
проведенной к графику функции в точке![]() ,
при приращении аргумента равном
,
при приращении аргумента равном![]() .
.
(Рис. 1).При
![]() имеем
имеем![]() ,
,
откуда получаем формулу приближенного вычисления значения функции в точке.
Пример. Найти
дифференциал функции
![]() .
.
Перепишем функцию
![]() в виде
в виде![]() .
Найдем
.
Найдем![]() .
.
![]() .
Тогда
.
Тогда
![]() .
.
Пример. Вычислить
приближенно
![]() .
.
Выберем точку
![]() и приращение
и приращение![]() так, чтобы
так, чтобы![]() был легко вычисляем, а
был легко вычисляем, а![]() было мало в сравнении с
было мало в сравнении с![]() .
Пусть
.
Пусть![]() ,
,![]() .
Для функции
.
Для функции![]() имеем:
имеем:![]() ,
,![]() ,
,![]() .
Тогда
.
Тогда![]()
![]()
![]()
![]() .
.
Дифференциалом второго порядка функции называется первый дифференциал первого дифференциала, то естьи он обозначаетсяили.
![]()
Соответственно
дифференциал n-ого
порядка
![]() ,
,![]() .
.
Дифференциалы 2-го и более высоких порядков сложных функций не обладают свойством инвариантности.
Задачи для самостоятельного решения
Найти дифференциал функции:
65.
![]() .
66.
.
66.![]() .
67.
.
67.![]() .
68.
.
68.![]() .
.
69. Выразить дифференциал
сложной функции через независимую
переменную и ее дифференциал:
![]() ,
,![]() .
.
Найти дифференциалы следующих неявно заданных функций:
70.
![]() .
71.
.
71.![]() .
.
72. Найти приближенное
значение приращения функции
![]() при
изменении
при
изменении![]() от
от![]() до
до![]() .
Чему равен
.
Чему равен![]() ?
?
73. Вычислить
приближенно: а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
74. Вычислить
приближенно:
 .
.
75.
![]() ,
,![]() ,
,![]() .
Выразить
.
Выразить![]() через а)
через а)![]() и
и![]() ,
б)
,
б)![]() и
и![]() ,
в)
,
в)![]() и
и![]() .
.
4.6. Теоремы о дифференцируемых функциях
Теорема Ролля.
Пусть функция
![]() непрерывна на
непрерывна на![]() ,
дифференцируема на
,
дифференцируема на![]() и
и![]() .
Тогда существует, по крайней мере, одна
точка
.
Тогда существует, по крайней мере, одна
точка![]() такая, что
такая, что![]() .
.
Теорема Лагранжа.
Пусть функция
![]() непрерывна на
непрерывна на![]() ,
дифференцируема на
,
дифференцируема на![]() .
Тогда существует, по крайней мере, одна
точка
.
Тогда существует, по крайней мере, одна
точка![]() такая, что
такая, что![]() .
.
Теорема Коши. Пусть
функции
![]() и
и![]() непрерывны на
непрерывны на![]() ,
дифференцируемы на
,
дифференцируемы на![]() и
и![]()
![]() .
Тогда существует, по крайней мере, одна
точка
.
Тогда существует, по крайней мере, одна
точка![]() такая, что
такая, что![]() .
.
Задачи для самостоятельного решения
76. Проверить
справедливость теоремы Ролля для функции
![]() в интервале
в интервале![]() .
.
77. Объяснить, почему
для функции
![]() ,
принимающей равные значения на концах
отрезка
,
принимающей равные значения на концах
отрезка![]() ,
не выполняется теорема Ролля.
,
не выполняется теорема Ролля.
78. Написать формулу
Лагранжа для функции
![]() в интервале
в интервале![]() .
.
79. Проверить
справедливость теоремы Лагранжа для
функции
![]() в интервале
в интервале![]() .
.
80. Записав формулу
Коши для
![]() и
и![]() на отрезке
на отрезке![]() ,
найти значение
,
найти значение![]() .
.
81. Проверить
справедливость формулы Коши для функций
![]() и
и![]() на отрезке
на отрезке![]() .
.
4.7 Правило Лопиталя - Бернулли
Правило Лопиталя
позволяет раскрывать неопределенности
типа
![]() и
и![]() .
.
Теорема Лопиталя.
Пусть функции
![]() и
и![]() дифференцируемы в некоторой окрестности
точки
дифференцируемы в некоторой окрестности
точки![]() ,
за исключением быть может самой точки
,
за исключением быть может самой точки![]() ,
и пусть
,
и пусть![]() в этой окрестности. Если функции
в этой окрестности. Если функции![]() и
и![]() являются одновременно бесконечно малыми
при
являются одновременно бесконечно малыми
при![]() (либо бесконечно большими при
(либо бесконечно большими при![]() )
и существует
)
и существует ,
то существует
,
то существует и имеет место равенство:
и имеет место равенство: =
=
Замечание.
Правило применимо и в случае, когда
 .
.Если производные
 и
и удовлетворяют условиям теоремы Лопиталя,
то к ним опять может быть применено это
правило.
удовлетворяют условиям теоремы Лопиталя,
то к ним опять может быть применено это
правило.Предел отношения функций может существовать, но не вычисляться по правилу Лопиталя. Рассмотрим
 .
Предел существует, так как
.
Предел существует, так как .
Однако для производных
.
Однако для производных и
и предел при
предел при не существует, и, следовательно, не
существует предел отношения этих
производных.
не существует, и, следовательно, не
существует предел отношения этих
производных.
Пример. Найти
 .
.
Имеем
 .
.
Пример.
Найти
![]() .
.
Применим правило
Лопиталя, предварительно заменив
![]() на эквивалентную ей при
на эквивалентную ей при![]() бесконечно малую функцию
бесконечно малую функцию![]() .
.
 применяя
правило Лопиталя)=
применяя
правило Лопиталя)=
![]()
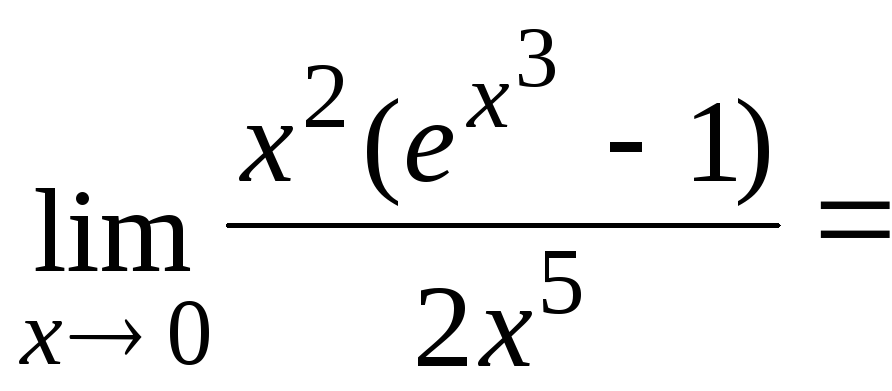
![]() при
при
![]() )=
)=![]() .
.
Пример.
Найти
![]() .
.
Имеем неопределенность
типа
![]() .
“Перестроим” функцию:
.
“Перестроим” функцию:![]()
 применяем
правило Лопиталя)=
применяем
правило Лопиталя)=![]() .
.
Пример.
Найти
![]() .
.
Имеем неопределенность
типа
![]() .
Логарифмируя функцию
.
Логарифмируя функцию![]() ,
получаем
,
получаем![]() .
.![]() ,
применяем правило Лопиталя)=
,
применяем правило Лопиталя)=![]() ==
==![]() ,
еще раз применяем правило Лопиталя)=
,
еще раз применяем правило Лопиталя)=
=![]() =
=![]() =ln
2. Следовательно,
=ln
2. Следовательно,![]() =
=
=
=![]() .
.
