
- •Передмова
- •1. Перестановки та підстановки
- •1, 2, …, N.
- •2. Визначники
- •2.1. Матриці. Загальні відомості
- •2.2. Визначники другого та третього порядків
- •2.3. Визначники n-го порядку
- •2.4. Властивості визначників
- •2.5. Мінори та їх алгебраїчні доповнення
- •2.6. Розклад визначника за елементами рядка або стовпця
- •2.7. Знаходження визначника зведенням до трикутного виду
- •3. Алгебра матриць
- •3.1. Додавання матриць і множення матриці на число
2.1. Матриці. Загальні відомості
Матрицею
називається
прямокутна таблиця, заповнена деякими
математич-ними об’єктами
(символами). Якщо матриця має k
рядків і n
стовпців, то говорять, що вона має розмір
k
n.
Елементи матриці позначатимемо однією
буквою з двома індексами, які вказують
на місце елемента в матриці: перший
індекс означає номер рядка, в якому
знаходиться даний елемент, а другий
індекс вказує місце елемента в рядку,
тобто номер стовпця, в якому міститься
даний елемент. Матриця розміру
k
n
з
елементами
![]() записується в такій формі:
записується в такій формі:
 ,
або
,
або
 .
.
Для
позначення матриці A
розміру
k
n
з
елементами
![]() також
використовують скорочений запис
також
використовують скорочений запис
![]() .
.
Далі ми будемо розглядати матриці з елементами з множини R дійсних чисел.
Дві
матриці
![]() і
і
![]() називаються
рівними,
якщо
називаються
рівними,
якщо
![]() для кожної пари індексівi,
j
(1
i
k,
1
j
n).
Інакше кажучи, рівні матриці мають
однакові розміри, а їх елементи, що
стоять на тих самих місцях, мають
збігатись.
для кожної пари індексівi,
j
(1
i
k,
1
j
n).
Інакше кажучи, рівні матриці мають
однакові розміри, а їх елементи, що
стоять на тих самих місцях, мають
збігатись.
Якщо кількість рядків матриці дорівнює кількості її стовпців, то така матриця називається квадратною, а кількість її рядків ( або стовпців ) називається порядком квадратної матриці.
Наприклад,
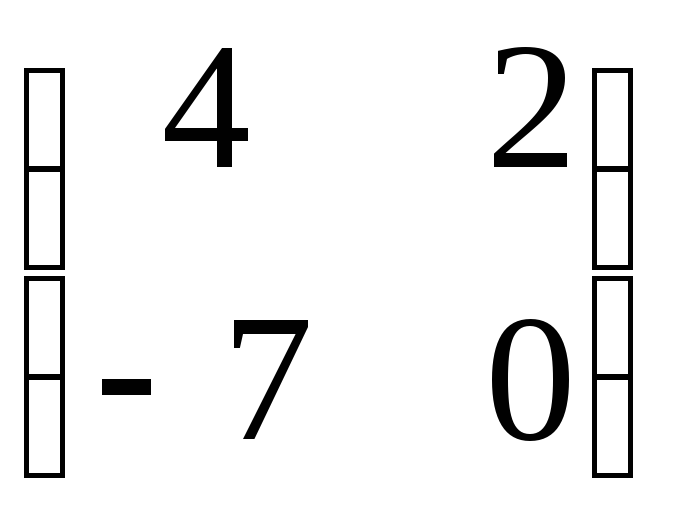 квадратна
матриця другого порядку.
квадратна
матриця другого порядку.
Зокрема, квадратна матриця порядку 1 – це просто один елемент.
Для
квадратної матриці вводяться поняття
головної та бічної діагоналей. Будемо
називати головною
діагоналлю
матриці
![]() упорядковану сукупність елементів
упорядковану сукупність елементів
![]() ,
що йдуть із лівого верхнього кута цієї
матриці до правого нижнього її кута.Бічною
діагоналлю
матриці
,
що йдуть із лівого верхнього кута цієї
матриці до правого нижнього її кута.Бічною
діагоналлю
матриці
![]() називається упорядкована сукупність
елементів
називається упорядкована сукупність
елементів
![]() ,
які йдуть із лівого нижнього кута матриці
до правого верхнього її кута.
,
які йдуть із лівого нижнього кута матриці
до правого верхнього її кута.
Слідом
квадратної матриці називається сума
елементів її головної діагоналі. Слід
матриці А
позначається через trA.
Отже, якщо
![]() ,
то
,
то
![]() .
.
Наприклад, якщо
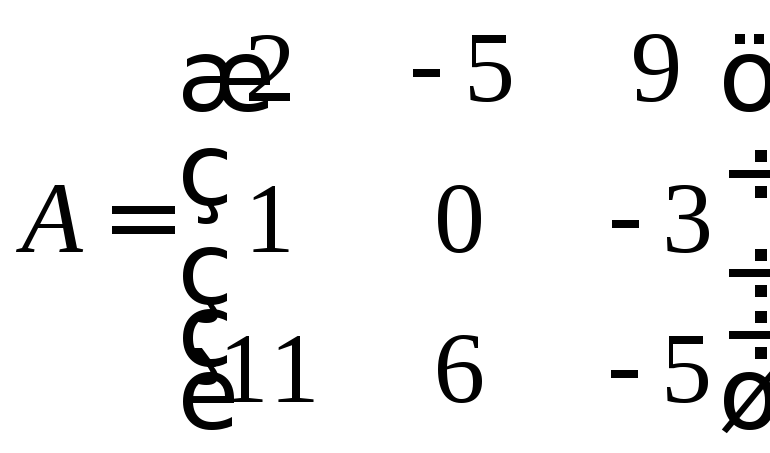 ,
,
то
![]() .
.
Числова
квадратна матриця
![]() називається верхньою
трикутною,
якщо
називається верхньою
трикутною,
якщо
![]() дляi
> j.
дляi
> j.
Так,

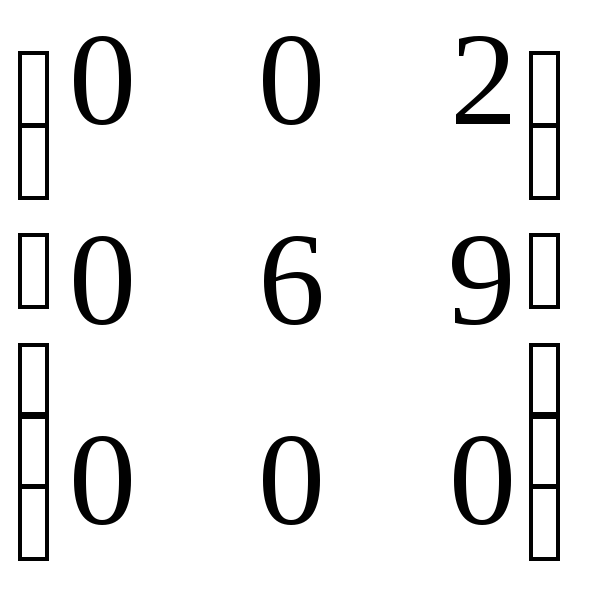 верхні
трикутні матриці порядку 3.
верхні
трикутні матриці порядку 3.
Числова
квадратна матриця
![]() називається нижньою
трикутною,
якщо
називається нижньою
трикутною,
якщо
![]() дляi
j.
дляi
j.
Прикладом нижньої трикутної матриці другого порядку є матриця
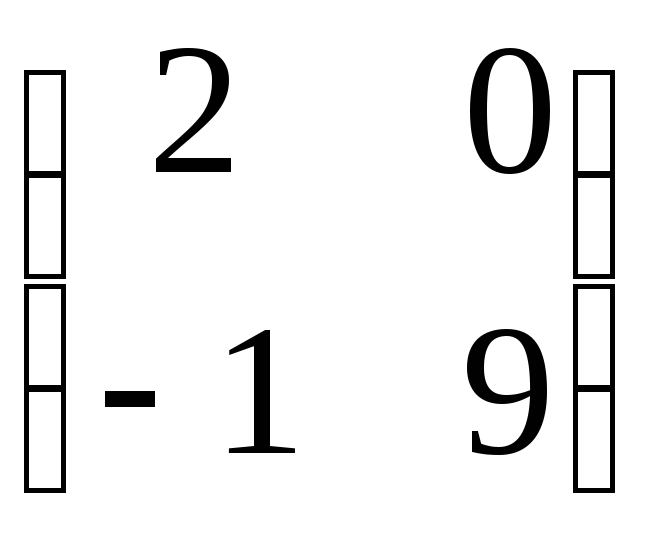 .
.
Числова
квадратна матриця
![]() називається діагональною,
якщо
називається діагональною,
якщо
![]() дляi
j
(1
i,
j
n).
дляi
j
(1
i,
j
n).
Наприклад,
 діагональна
матриця порядку 2.
діагональна
матриця порядку 2.
Діагональна
матриця D
з елементами
![]() на головній діагоналі позначається
на головній діагоналі позначається![]() .
.
Так,
 .
.
Діагональна матриця, елементи головної діагоналі якої однакові, називається скалярною. Наприклад,
 –скалярна
матриця другого порядку.
–скалярна
матриця другого порядку.
Нехай
![]() .
Транспонуванням
матриці
А
називається
перехід до матриці
.
Транспонуванням
матриці
А
називається
перехід до матриці
![]() ,
де
,
де
![]() .
Інакше кажучи, рядки матриці
.
Інакше кажучи, рядки матриці![]() – це стовпці матриці А з відповідними
номерами, а стовпці матриці
– це стовпці матриці А з відповідними
номерами, а стовпці матриці![]() – це рядки матриціА
і якщо A
має розмір k
n,
то
– це рядки матриціА
і якщо A
має розмір k
n,
то
![]() –n
k.
Матриця
–n
k.
Матриця
![]() називається матрицею,
транспонованою
до А.
називається матрицею,
транспонованою
до А.
Наприклад, якщо
 ,
,
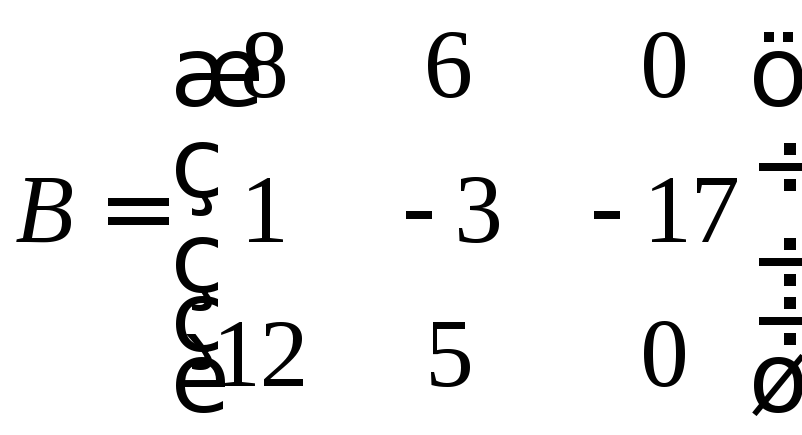 ,
,
то
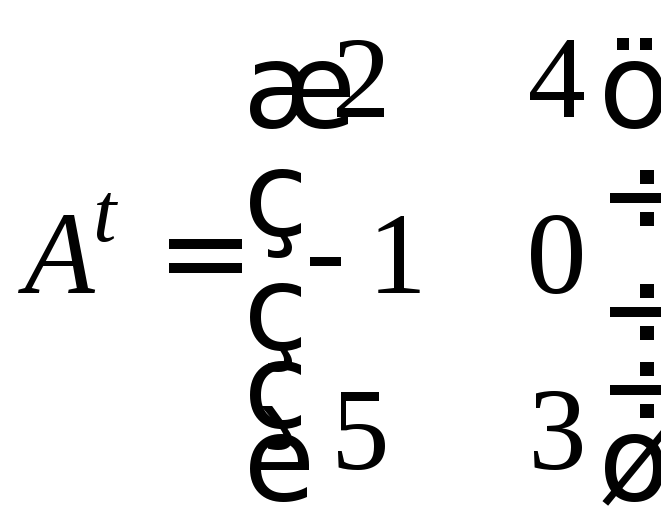 ,
,
 .
.
2.2. Визначники другого та третього порядків
Розглянемо довільну квадратну матрицю n-го порядку:
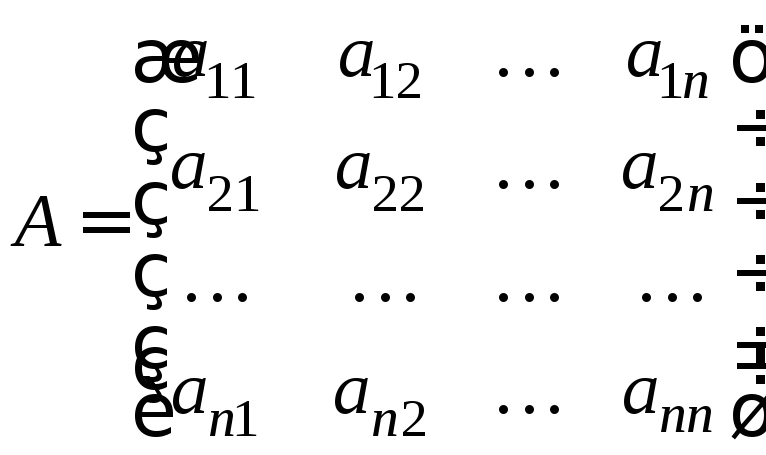 .
.
З кожною такою матрицею можна пов’язати цілком визначену численну характеристику, яка називається визначником, відповідним цій матриці. Визначник матриці A позначається detA або |A|.
Також
для визначника матриці
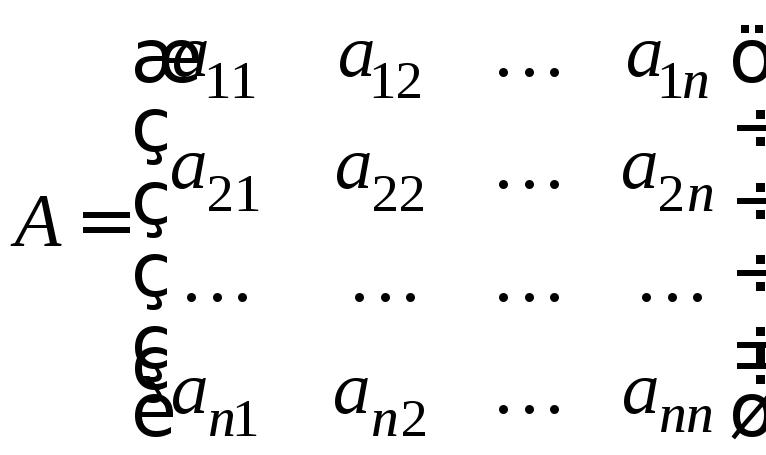 використовується запис
використовується запис
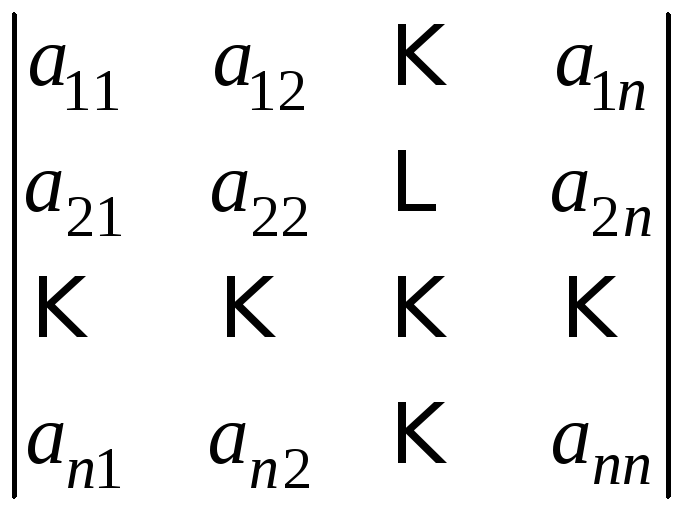 .
.
Якщо A – матриця першого порядку, тобто A складається з одного елемента, то визначником першого порядку, відповідним цій матриці, називається величина цього елемента.
Отже,
коли
![]() ,
то
,
то
![]() .
.
Якщо порядок матриці A дорівнює двом, тобто
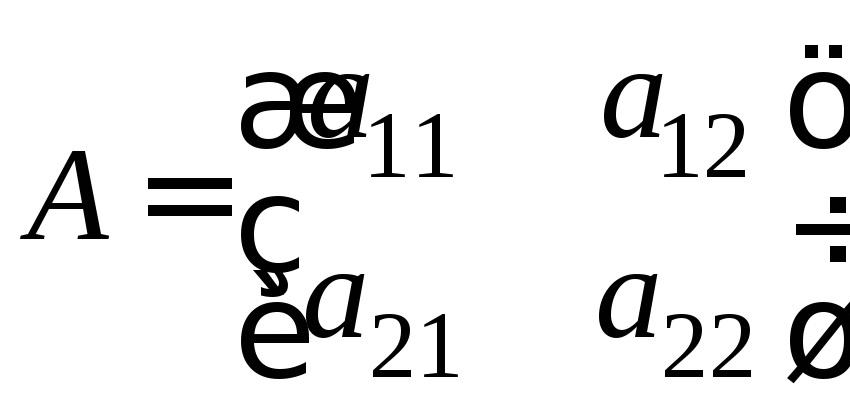 ,
,
то
визначником
другого порядку,
відповідним A,
називається
число, яке
дорівнює
![]() ,
отже,
,
отже,
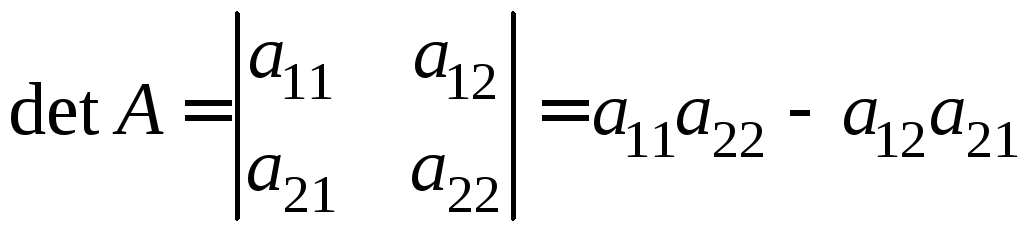 .
.
Розглянемо квадратну матрицю третього порядку
 .
.
Визначником (детермінантом) третього порядку, відповідним до матриці A називається число, яке добувається з виразу
![]() .
(1)
.
(1)
Отже,
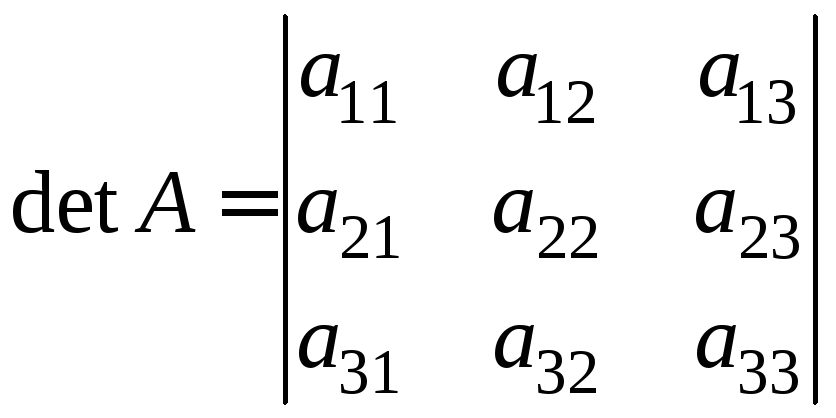 =
=
=
![]() .
.
Цю формулу можна запам’ятати за допомогою правила трикутника. Перші три члени, що входять до правої частини виразу (1) із знаком «+» є відповідно добуток елементів головної діагоналі і добутки елементів, розташованих у вершинах трикутників, основи яких паралельні цій діагоналі. Четвертий, п’ятий та шостий члени, які входять до виразу із знаком «–» є добуток елементів бічної діагоналі і добутки елементів, які є вершинами трикутників з основами, паралельними бічній діагоналі. Це правило можна зобразити схемою
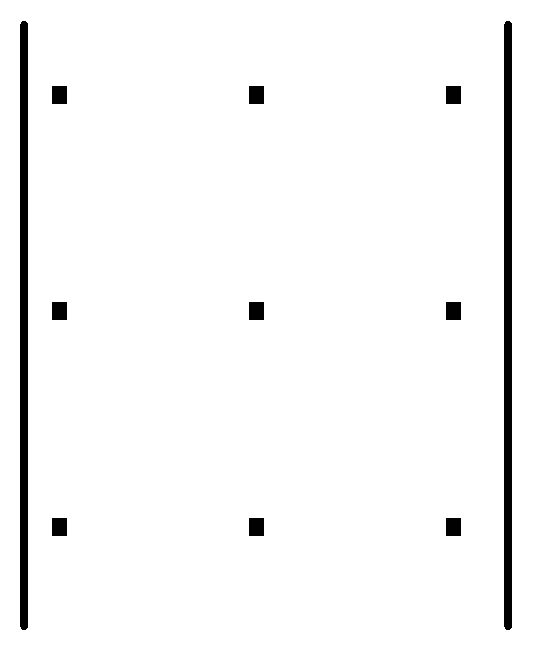

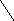
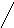




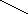





 =
=
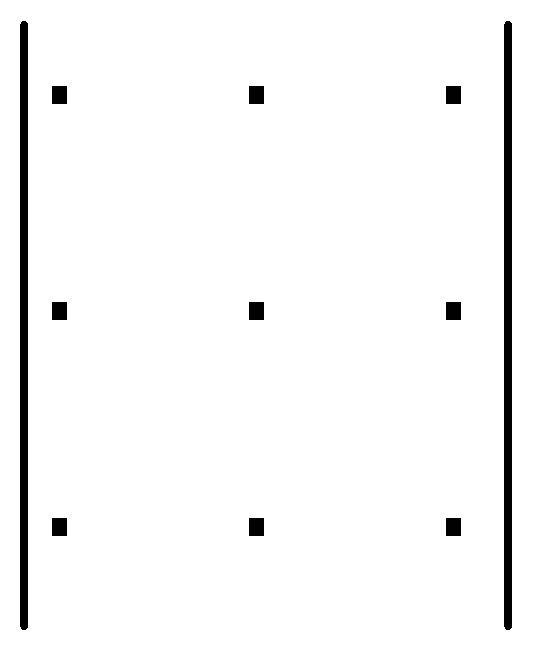 +
+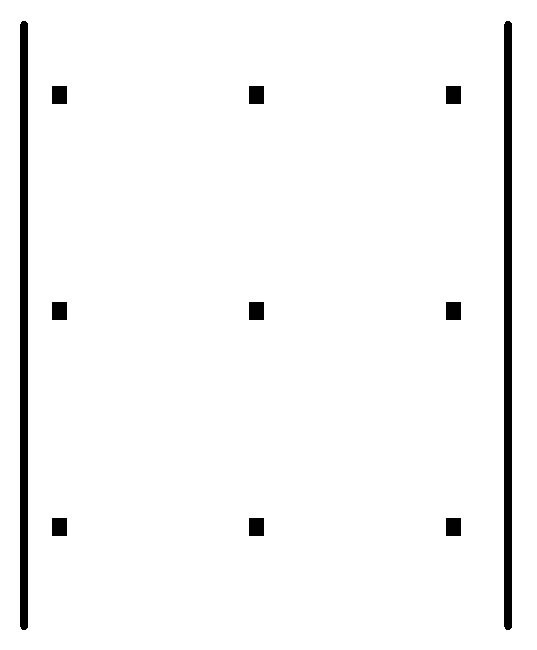 +
+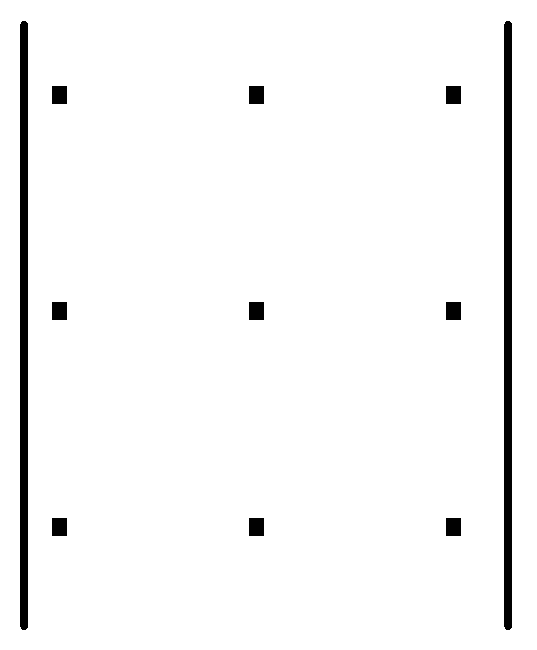 –
–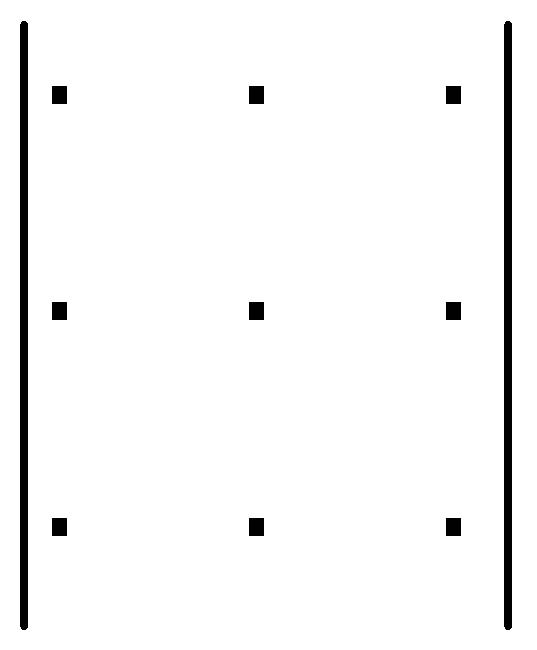 –
–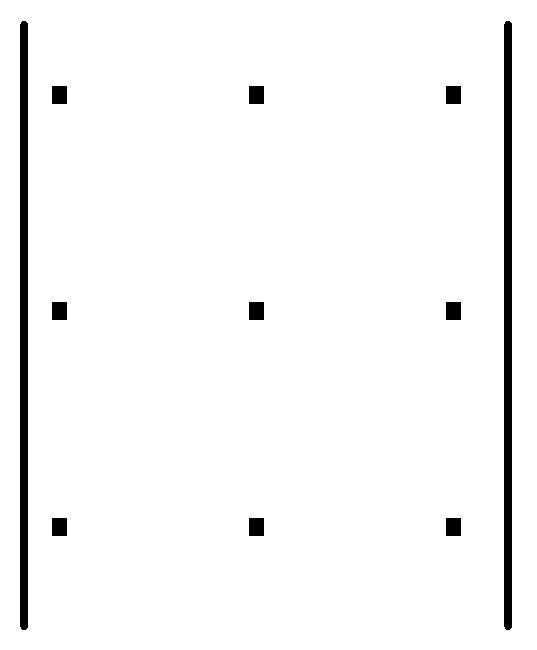 –
–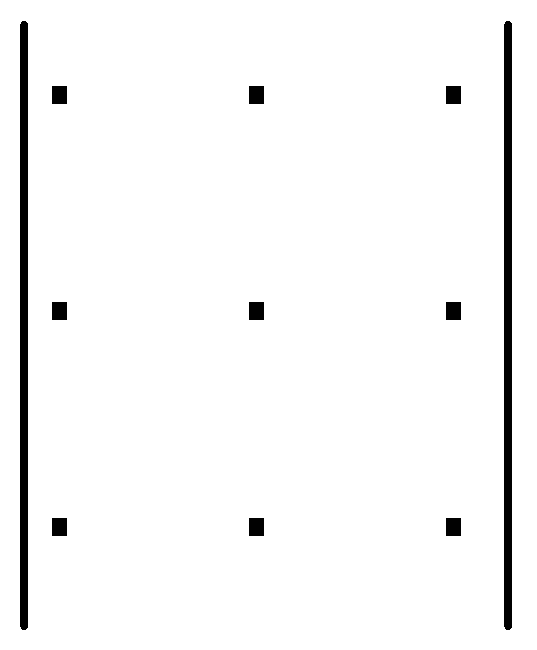 .
.
Приклад 2.1. Знайдемо такі визначники:
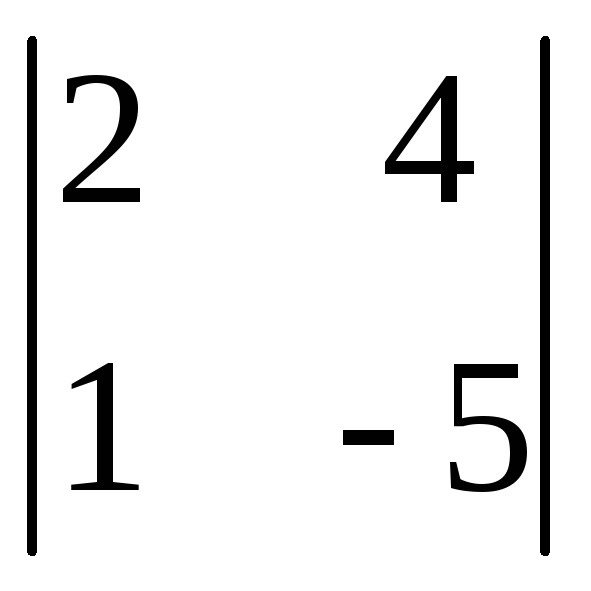 ,
,
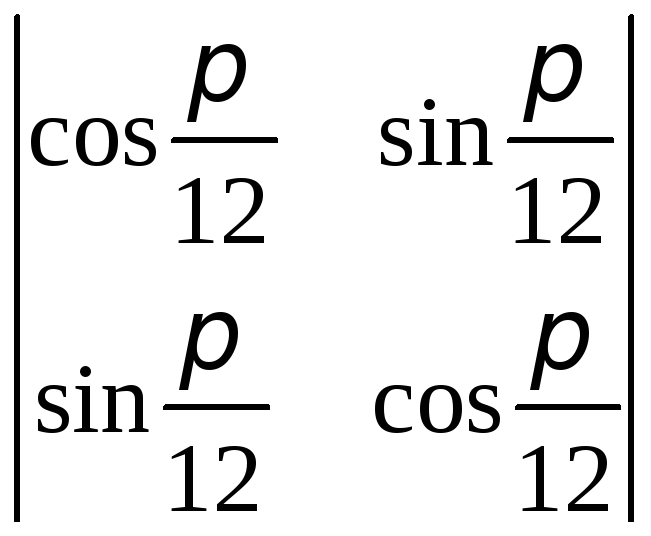 ,
,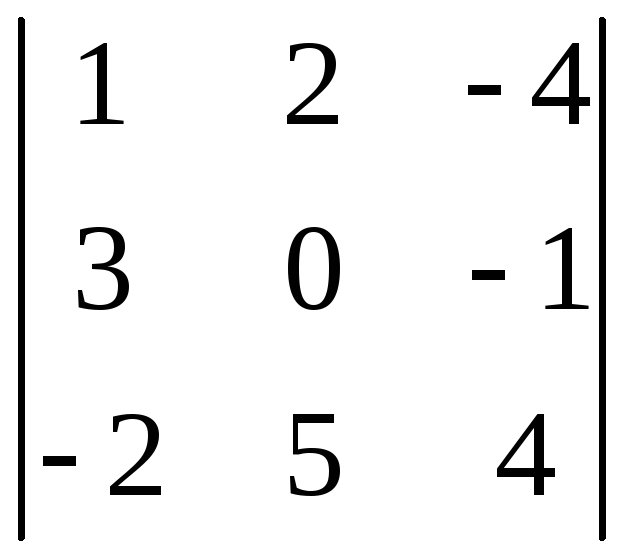 ,
,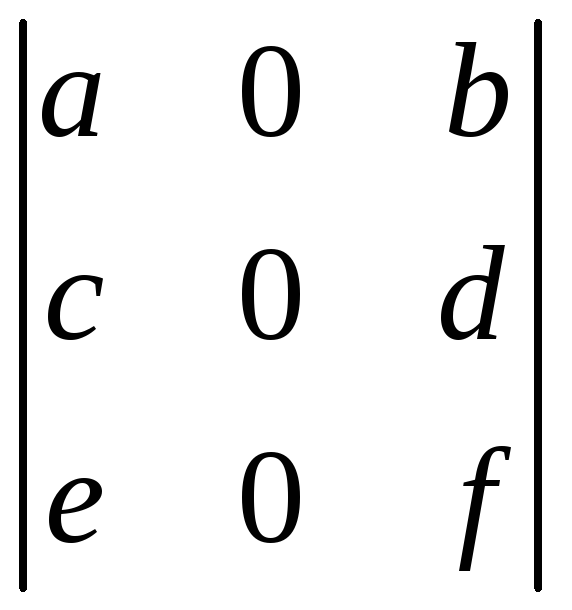 .
.
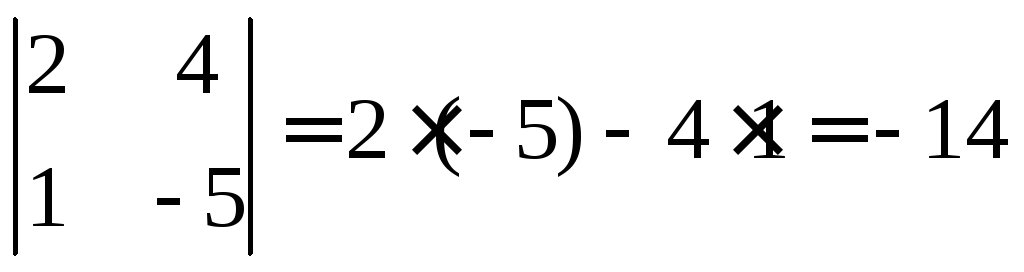 ;
;
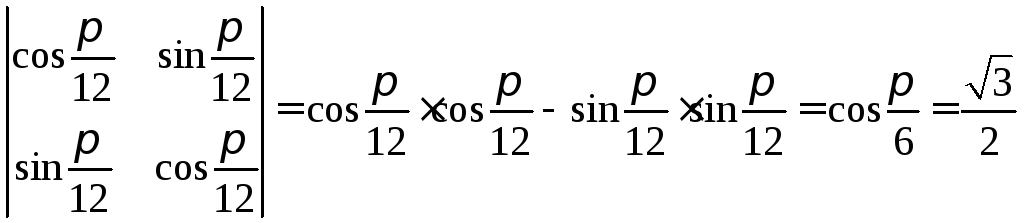 ;
;
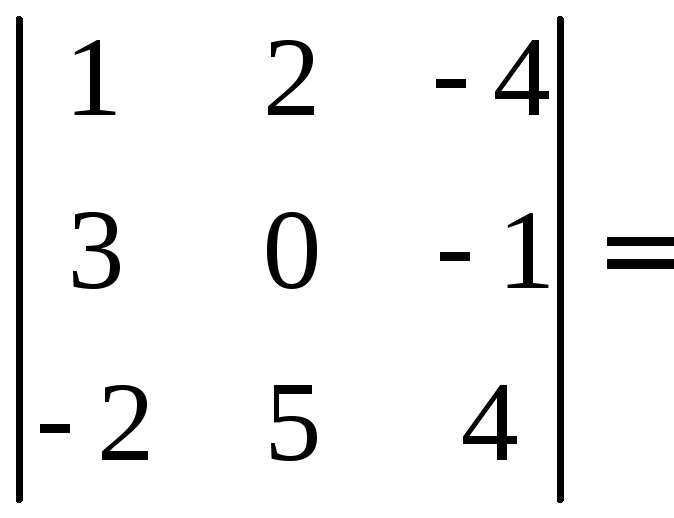
![]() ;
;
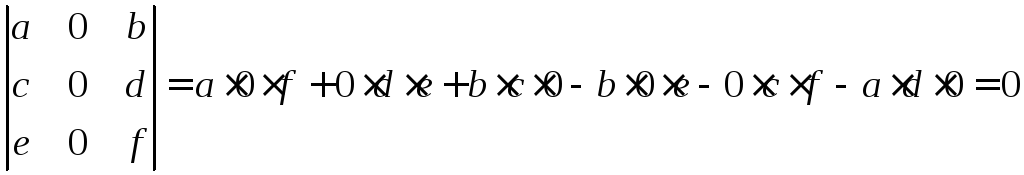 .
.
Задача 2.1. Обчислити визначники:
а)
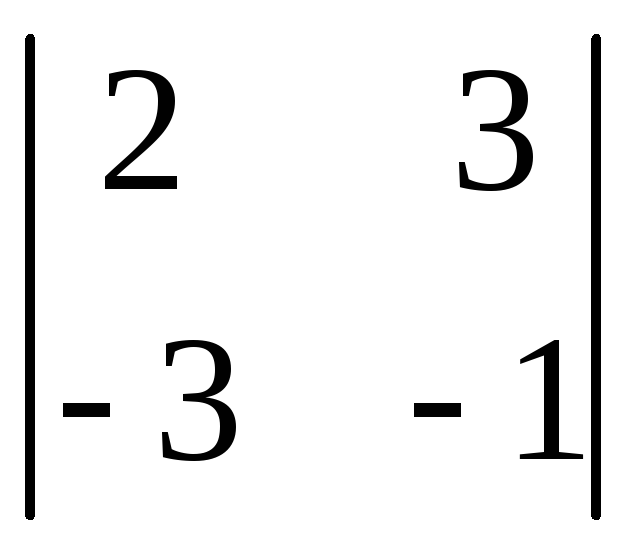 ;б)
;б)
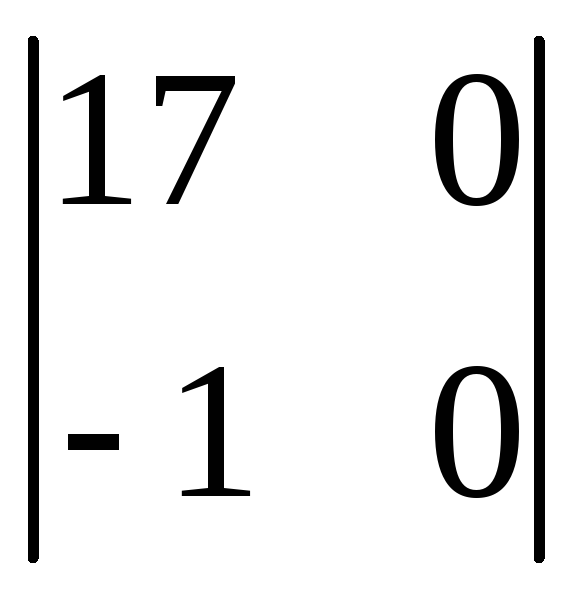 ;в)
;в)
![]() ;г)
;г)
![]() ;д)
;д)
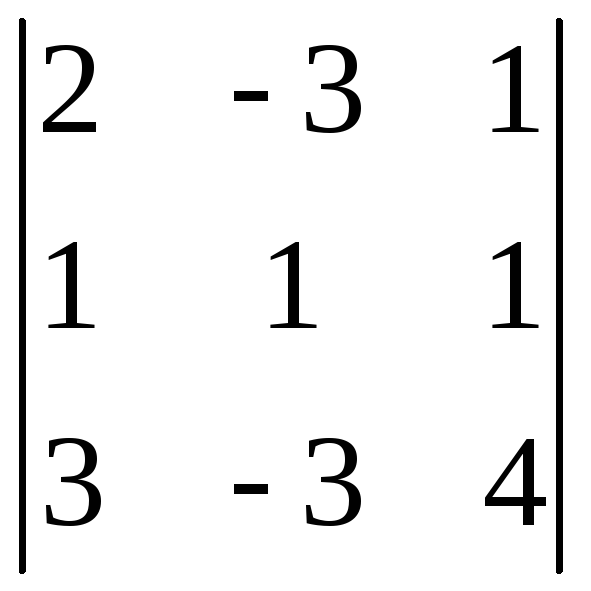 ;е)
;е)
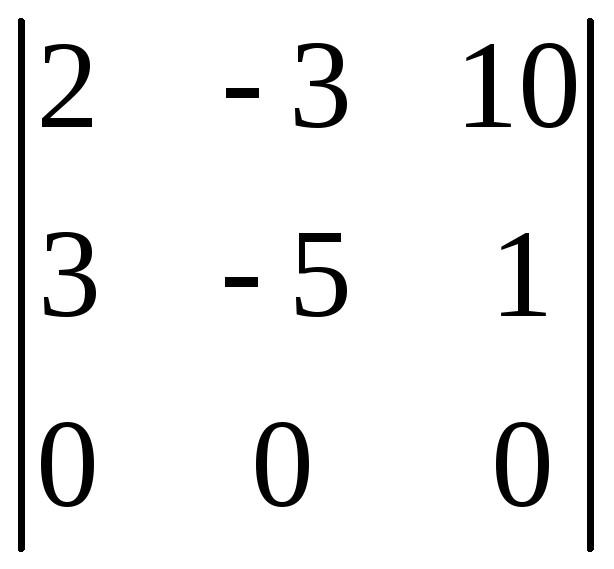 ;
;
є)
 ;ж)
;ж)
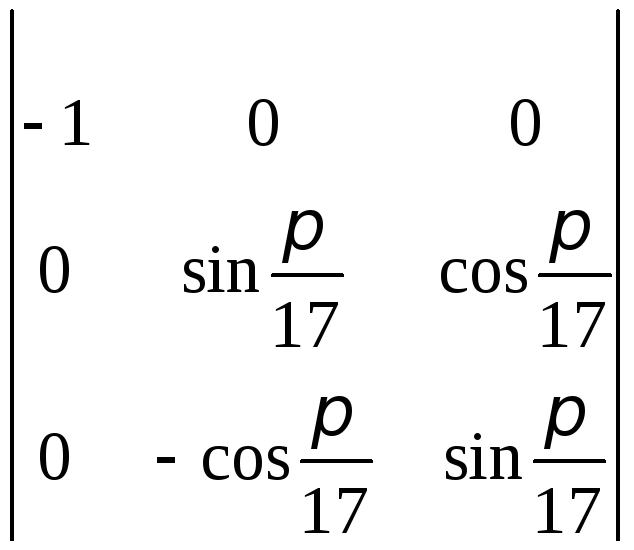 ;з)
;з)
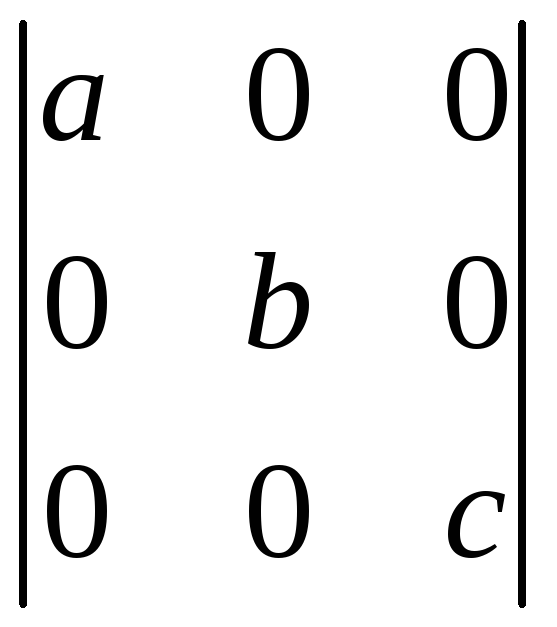 ;і)
;і)
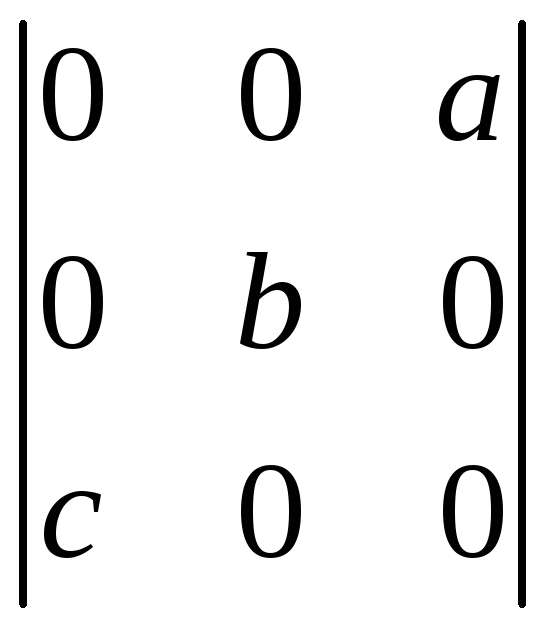 ;
;
к)
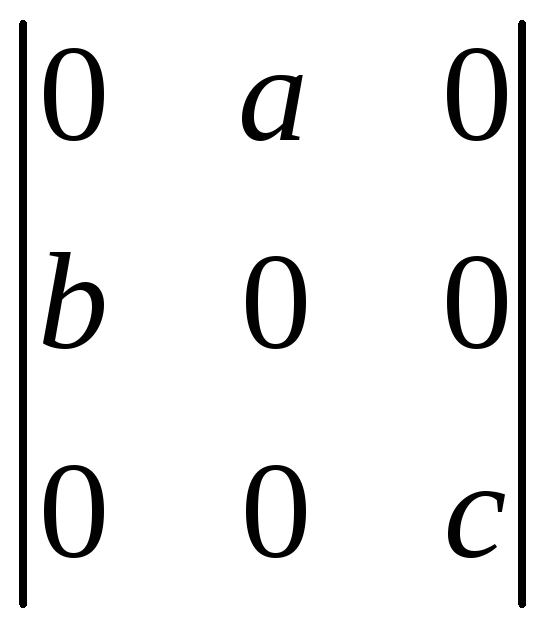 ;л)
;л)
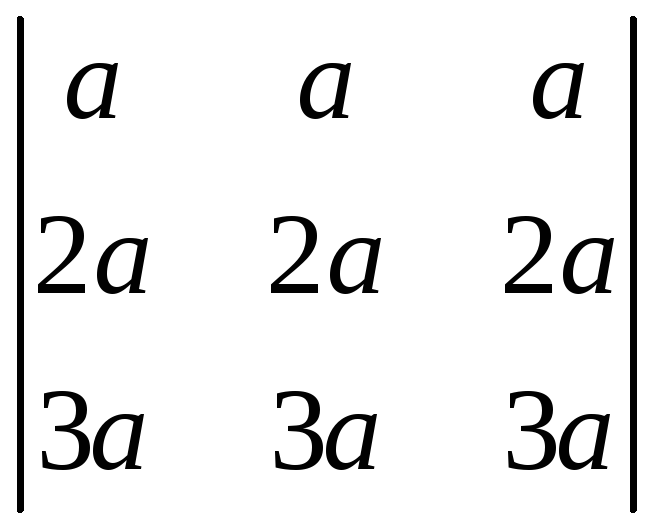 ;м)
;м)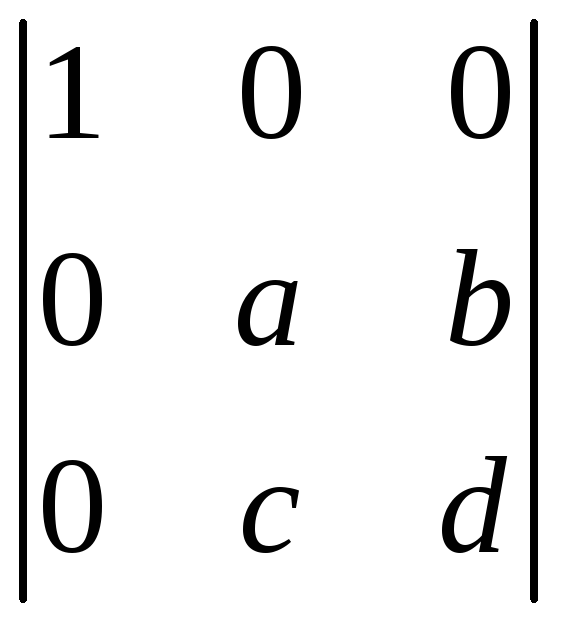 ;н)
;н)
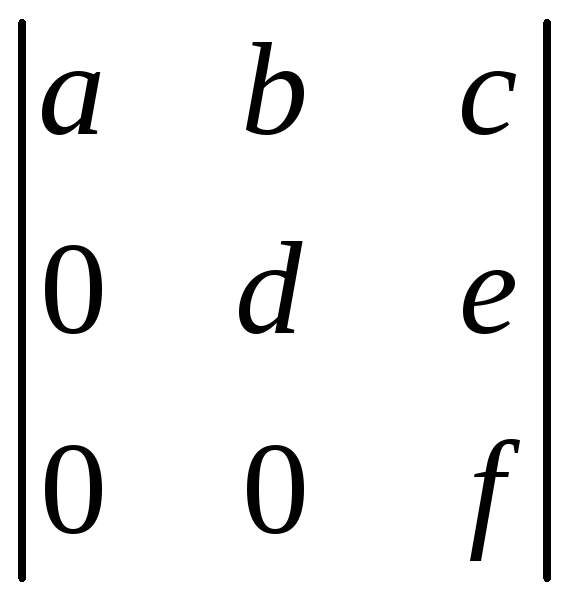 ;
о)
;
о)
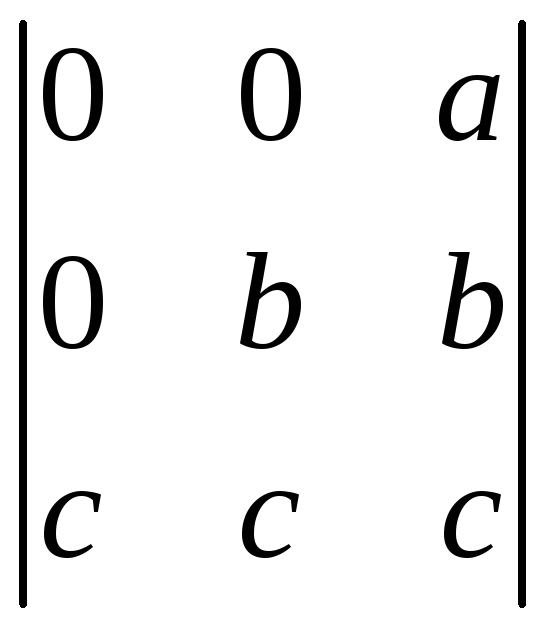 .
.
