
- •Передмова
- •1. Перестановки та підстановки
- •1, 2, …, N.
- •2. Визначники
- •2.1. Матриці. Загальні відомості
- •2.2. Визначники другого та третього порядків
- •2.3. Визначники n-го порядку
- •2.4. Властивості визначників
- •2.5. Мінори та їх алгебраїчні доповнення
- •2.6. Розклад визначника за елементами рядка або стовпця
- •2.7. Знаходження визначника зведенням до трикутного виду
- •3. Алгебра матриць
- •3.1. Додавання матриць і множення матриці на число
2.4. Властивості визначників
Властивість 1. Визначник не змінюється при транспонуванні, тобто
![]() .
.
Доведення.
Нехай
![]() .
Всякий член визначника матриці A
має
вигляд
.
Всякий член визначника матриці A
має
вигляд
![]() ,
де
,
де
![]() – деяка підстановка степеняn.
– деяка підстановка степеняn.
Усі
множники добутку
![]() знаходяться в різних рядках і різних
стовпцях матриціA.
Вони залишаться в різних рядках і різних
стовпцях також і в матриці AT,
а, значить, цей добуток є членом також
і визначника матриці
AT.
Аналогічно отримуємо, що кожен член
визначника AT
є
також членом визначника A.
Отже, визначники матриць A
і AT
складаються
із однакових членів.
знаходяться в різних рядках і різних
стовпцях матриціA.
Вони залишаться в різних рядках і різних
стовпцях також і в матриці AT,
а, значить, цей добуток є членом також
і визначника матриці
AT.
Аналогічно отримуємо, що кожен член
визначника AT
є
також членом визначника A.
Отже, визначники матриць A
і AT
складаються
із однакових членів.
Знак
добутку
![]() у визначникуA
визначається
парністю підстановки
у визначникуA
визначається
парністю підстановки
![]() .
У визначникуAT
цьому
добутку відповідає підстановка
.
У визначникуAT
цьому
добутку відповідає підстановка
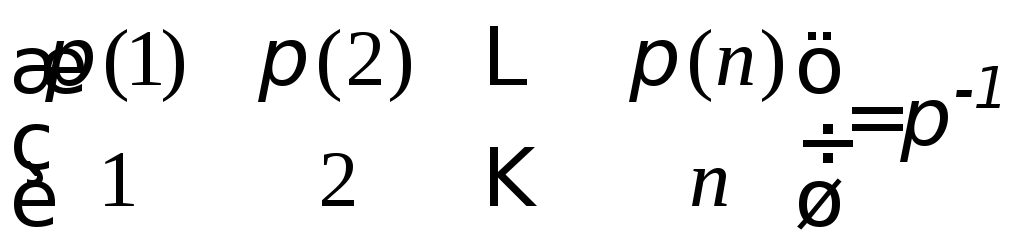 .
.
Оскільки
парності підстановок
![]() і
і![]() співпадають, то вказаний добуток входить
до розкладу визначникаAT
з
тим же знаком, що і до визначника матриці
A.
співпадають, то вказаний добуток входить
до розкладу визначникаAT
з
тим же знаком, що і до визначника матриці
A.
Таким чином, визначники матриць A і AT є сумами однакових членів, узятих з однаковими знаками, а, значить, ці визначники співпадають.
Наприклад,
 .
.
Із властивості 1 виходить, що всяке твердження, яке стосується рядків визначника, є вірним також і для стовпців і навпаки. Тому властивості 2 – 9 будуть сформульовані та доведені лише для рядків визначника, але вони є справедливими також і для стовпців.
Властивість 2. Якщо один із рядків визначника складається з нулів, то визначник дорівнює нулю.
Доведення. Нехай всі елементи k-го рядка визначника дорівнюють нулю. Кожен член цього визначника є добутком елементів, один із яких є елементом
k-го рядка. Отже, кожен член визначника дорівнює нулю, а, значить, і визначник дорівнює нулю.
Властивість 3. Якщо у визначнику поміняти місцями два рядки, то визначник змінить знак.
Доведення. Нехай k < m. У визначнику
 (1)
(1)
переставимо k-й та m-й рядки. Тоді отримаємо визначник
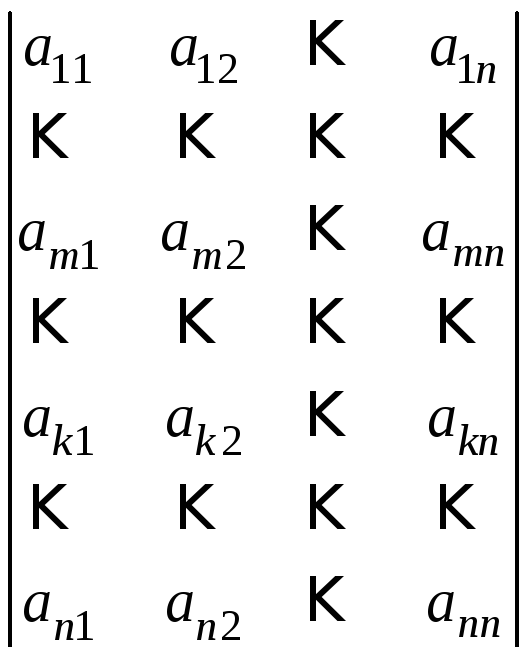 (2).
(2).
Якщо
![]() (
(![]() – деяка підстановкаn-го
степеня) – член визначника (1), то всі
його множники залишаються в різних
рядках і різних стовпцях і у визначнику
(2). Тобто визначники (1) і (2) складаються
з однакових членів. Члену
– деяка підстановкаn-го
степеня) – член визначника (1), то всі
його множники залишаються в різних
рядках і різних стовпцях і у визначнику
(2). Тобто визначники (1) і (2) складаються
з однакових членів. Члену
![]() у визначнику (1) відповідає підстановка
у визначнику (1) відповідає підстановка
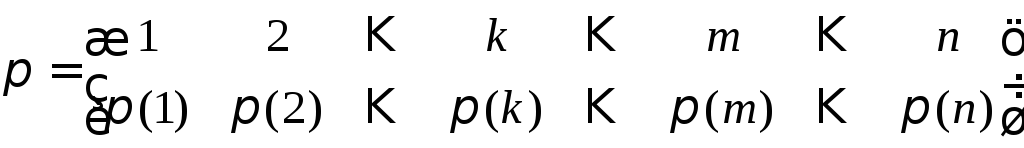 ,
,
а у визначнику (2) – підстановка
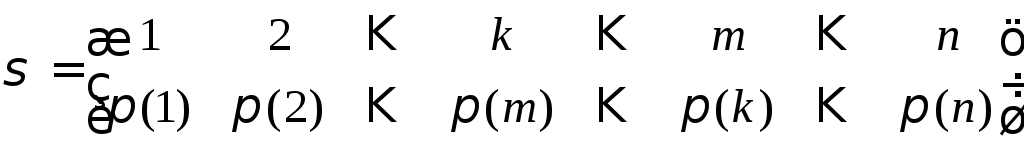 .
.
Підстановки
![]() і
і![]() мають протилежні парності ( див., напр.,
[3]). Звідси виходить, що всі члени
визначника (1) входять до розкладу
визначника (2) із протилежними знаками,
тобто визначники (1) і (2) відрізняються
лише знаком.
мають протилежні парності ( див., напр.,
[3]). Звідси виходить, що всі члени
визначника (1) входять до розкладу
визначника (2) із протилежними знаками,
тобто визначники (1) і (2) відрізняються
лише знаком.
Наприклад,
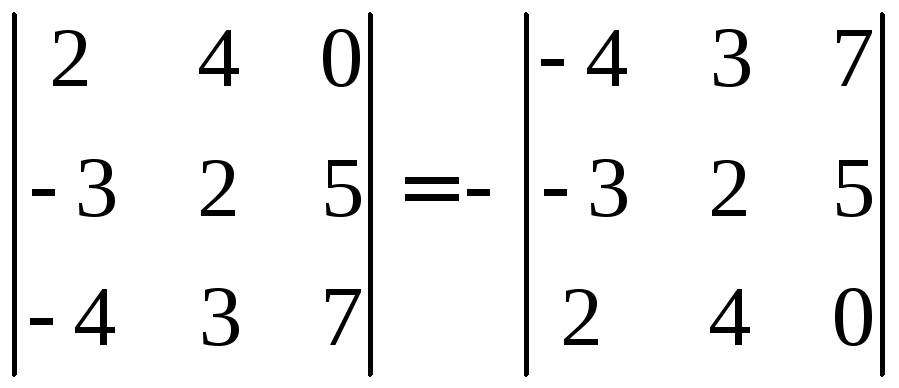 .
.
Властивість 4. Визначник, який містить два однакових рядки, дорівнює нулю.
Доведення. Нехай визначник дорівнює числу d і нехай відповідні елементи k-го та m-го рядків рівні між собою. Якщо поміняти місцями ці рядки, то за властивістю 3, змінений визначник буде дорівнювати (– d). Оскільки міняються місцями рівні рядки, то значення визначника не змінюється, а, значить, d = – d, звідки d = 0.
Наприклад,
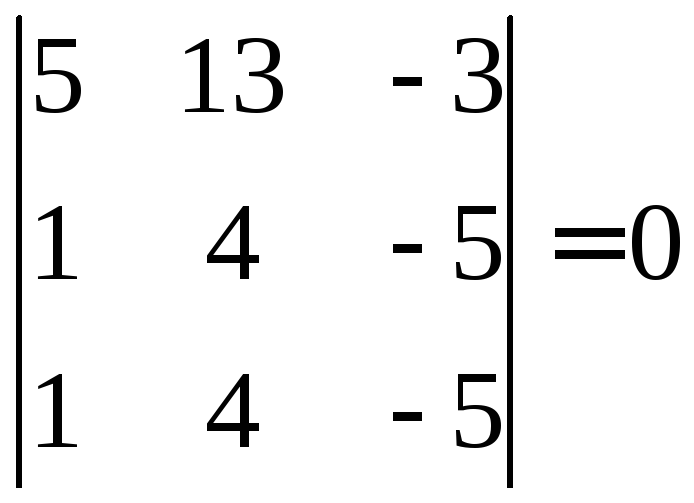 .
.
Властивість
5.
Якщо
всі елементи одного з рядків визначника
помножити на деяке число
![]() ,
то сам визначник помножиться на
,
то сам визначник помножиться на![]() .
.
Доведення.
Нехай всі елементи k-го
рядка визначника помножені на
![]() .
Кожен член визначника містить у точності
один елемент ізk-го
рядка, а тому після вказаного перетворення
кожен член визначника помножиться на
.
Кожен член визначника містить у точності
один елемент ізk-го
рядка, а тому після вказаного перетворення
кожен член визначника помножиться на
![]() ,
а, значить, і визначник помножиться на
,
а, значить, і визначник помножиться на![]() .
.
Властивість 5 можна сформулювати по-іншому: спільний множник елементів деякого рядка можна винести за знак визначника.
Наприклад,
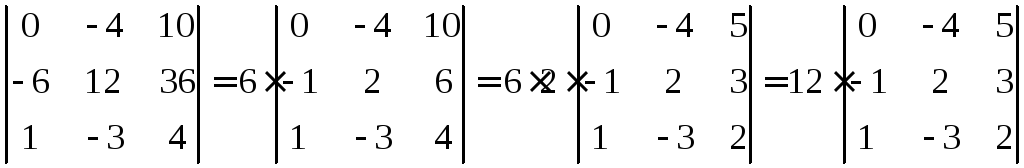 –
–
із другого рядка визначника ми винесли число 6, а потім із третього стовпця – число 2.
Властивість 6. Визначник, який містить два пропорційних рядки, дорівнює нулю.
Доведення.
Нехай визначник дорівнює числу d
і нехай елементи k-го
рядка визначника дорівнюють відповідним
елементам m-го
рядка (k
≠
m),
помноженим на деяке число
![]() .
За властивістю 5 число
.
За властивістю 5 число![]() можна винести ізk-го
рядка за знак визначника, тобто
можна винести ізk-го
рядка за знак визначника, тобто
![]() ,
,
де d1 – визначник, в якому k-й та m-й рядки співпадають. За властивістю 4 d1 = 0, а, значить,
![]() .
.
Наприклад,
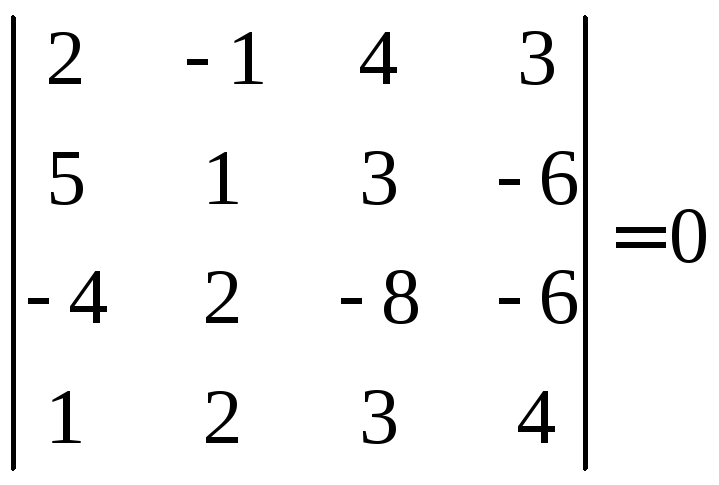 ,
,
оскільки елементи третього рядка дорівнюють відповідним елементам першого рядка, помноженим на (–2).
Властивість 7. Якщо всі елементи k-го рядка визначника n-го порядку подані у вигляді суми двох доданків
![]() ,
,
то
визначник дорівнює сумі двох визначників,
де всі рядки, окрім k-го,
– такі ж, як і
у
заданому визначнику, а k-й
рядок в одному з визначників-доданків
складається з елементів
![]() ,
а в другому –
з
елементів
,
а в другому –
з
елементів
![]() .
.
Доведення.
Нехай
![]() (
(![]() – деяка підстановкаn-го
степеня) –член заданого визначника.
Тоді ми можемо подати його у вигляді
суми двох добутків:
– деяка підстановкаn-го
степеня) –член заданого визначника.
Тоді ми можемо подати його у вигляді
суми двох добутків:
![]()
![]() .
.
Розкладемо
в таку суму двох доданків кожен член
заданого визначника. Сума всіх перших
доданків з тими ж знаками, з якими вони
входять у заданий визначник, буде
дорівнювати визначнику n-го
порядку, який відрізняється від заданого
визначника лише тим, що в його k-му
рядку замість елементів
![]() знаходяться елементи
знаходяться елементи![]() .
Сума других доданків з тими ж знаками,
що і в заданому визначнику, складе
визначник, уk-му
рядку якого знаходяться елементи
.
Сума других доданків з тими ж знаками,
що і в заданому визначнику, складе
визначник, уk-му
рядку якого знаходяться елементи
![]() .
Отже,
.
Отже,
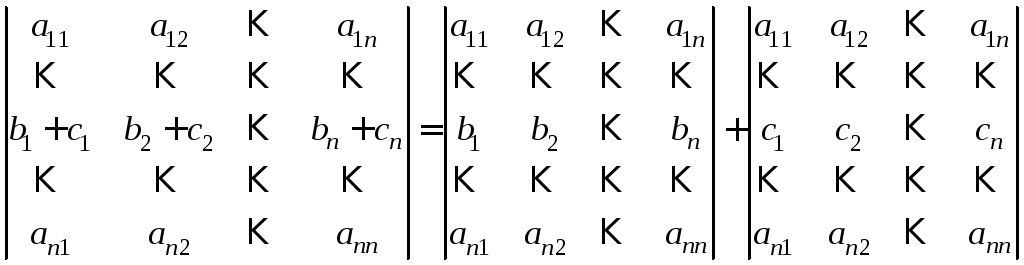 .
.
Наприклад,
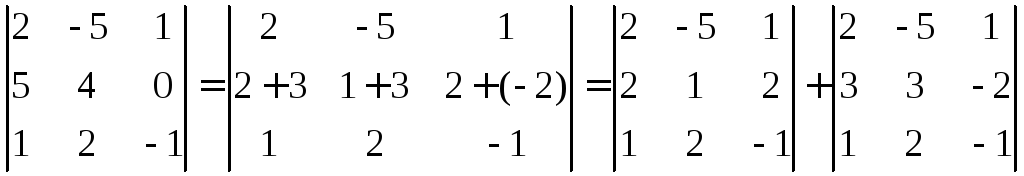 .
.
Нехай
![]() – квадратна матриця порядку n
з елементами
– квадратна матриця порядку n
з елементами
![]() .
Будемо говорити, що k-тий
рядок
.
Будемо говорити, що k-тий
рядок
![]() матриціA
є лінійною
комбінацією рядків з номерами
матриціA
є лінійною
комбінацією рядків з номерами
![]() з коефіцієнтами
з коефіцієнтами![]() ,
якщо
,
якщо
![]() для
всіх
для
всіх
![]() .
.
Наприклад, у матриці
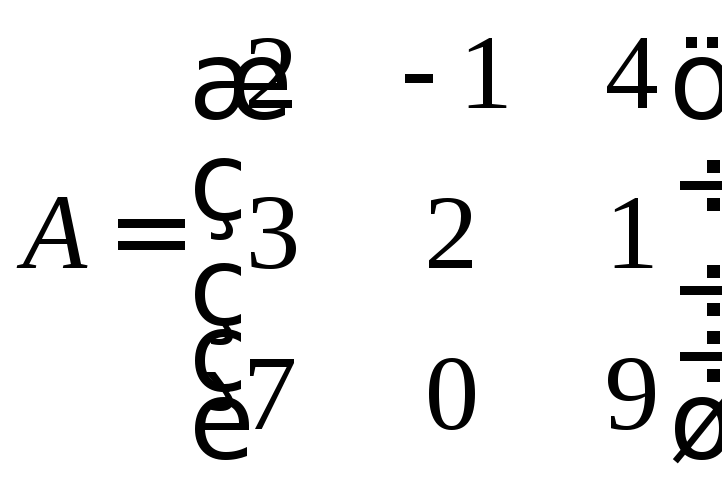
третій рядок є лінійною комбінацією першого і другого з коефіцієнтами 2 і 1.
Аналогічно визначається лінійна комбінація стовпців матриці.
Властивість 8. Якщо один із рядків визначника є лінійною комбінацією інших його рядків, то визначник дорівнює нулю.
Доведення.
Нехай k-тий
рядок визначника є лінійною комбінацією
рядків з номерами
![]() .
Тоді всякий елемент k-го
рядка є сумою s
доданків. За властивістю 7 ми можемо
визначник подати у вигляді суми s
визначників,
у кожному з яких k-тий
рядок буде пропорційний одному з інших
рядків. За властивістю 6 кожен з таких
визначників дорівнює нулю, а, значить,
дорівнює нулю і сума цих визначників.
.
Тоді всякий елемент k-го
рядка є сумою s
доданків. За властивістю 7 ми можемо
визначник подати у вигляді суми s
визначників,
у кожному з яких k-тий
рядок буде пропорційний одному з інших
рядків. За властивістю 6 кожен з таких
визначників дорівнює нулю, а, значить,
дорівнює нулю і сума цих визначників.
Наприклад,
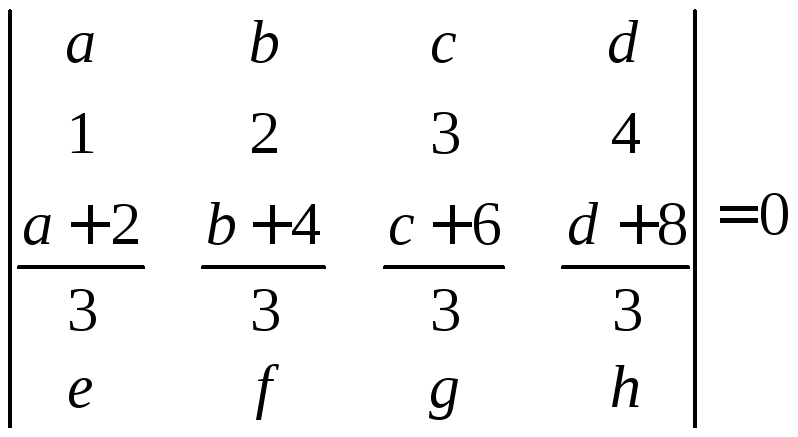 ,
,
оскільки
третій рядок визначника дорівнює
лінійній комбінації першого і другого
рядків з коефіцієнтами
![]() і
і![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() ).
).
Властивість 9. Визначник не зміниться, якщо до одного з його рядків додати відповідні елементи другого рядка, помножені на одне й те саме число.
Доведення.
Нехай d
– визначник
n-го
порядку з елементами
![]() (1
i,
j
n).
Припустимо, що до k-го
рядка визначника додається m-тий
рядок, помножений на число
(1
i,
j
n).
Припустимо, що до k-го
рядка визначника додається m-тий
рядок, помножений на число
![]() .
Тоді, в зміненому визначнику кожний
елементk-го
рядка, буде мати вигляд
.
Тоді, в зміненому визначнику кожний
елементk-го
рядка, буде мати вигляд
![]() ,
,![]() .
За властивістю 7 цей визначник можна
подати як суму двох визначників, перший
з яких співпадає з визначникомd,
а другий дорівнює нулю, оскільки містить
два пропорційних рядки.
.
За властивістю 7 цей визначник можна
подати як суму двох визначників, перший
з яких співпадає з визначникомd,
а другий дорівнює нулю, оскільки містить
два пропорційних рядки.
Наслідок. Визначник не зміниться, якщо до одного з його рядків додати лінійну комбінацію інших рядків.
Приклад
2.6.
Обчислити визначник
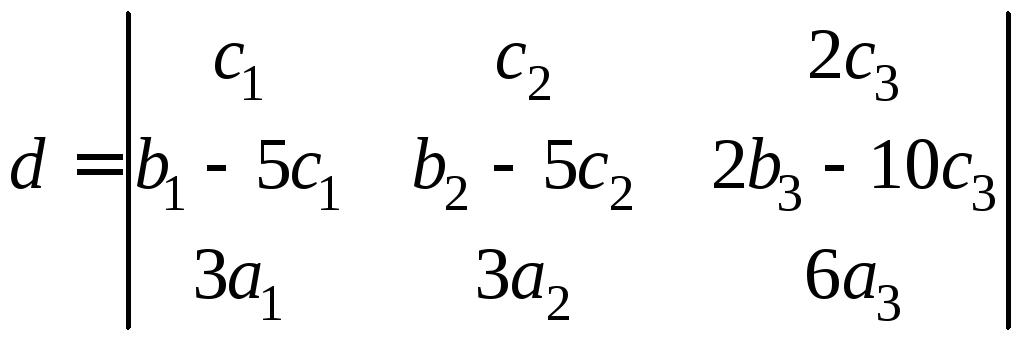 ,
якщо відомо, що
,
якщо відомо, що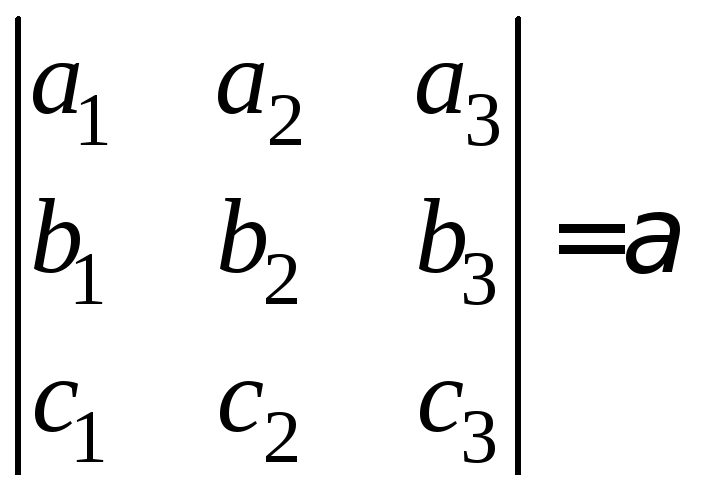 .
.
Здійснимо над визначником d послідовно такі дії:
1) із третього рядка винесемо число 3;
2) із третього стовпця винесемо число 2;
3) поміняємо місцями перший та третій рядки;
4) розкладемо отриманий визначник у суму двох доданків. Будемо мати:
d
=
 =
=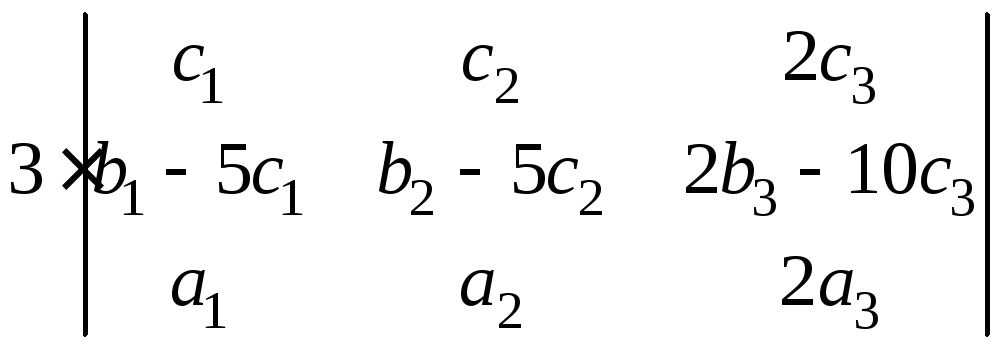 ==
==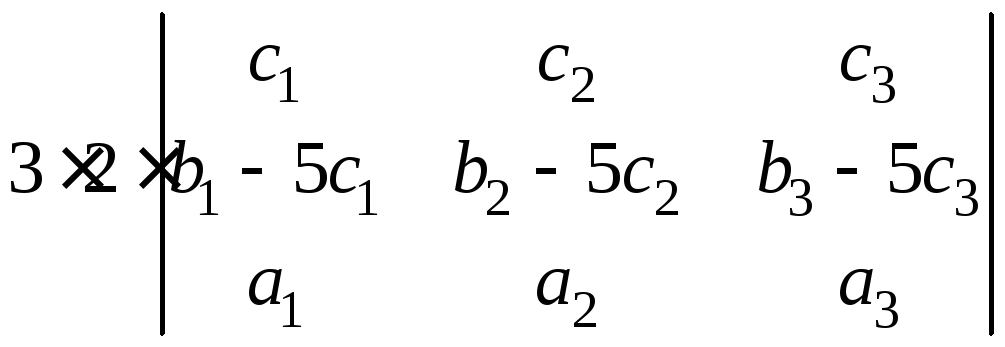 = –
= –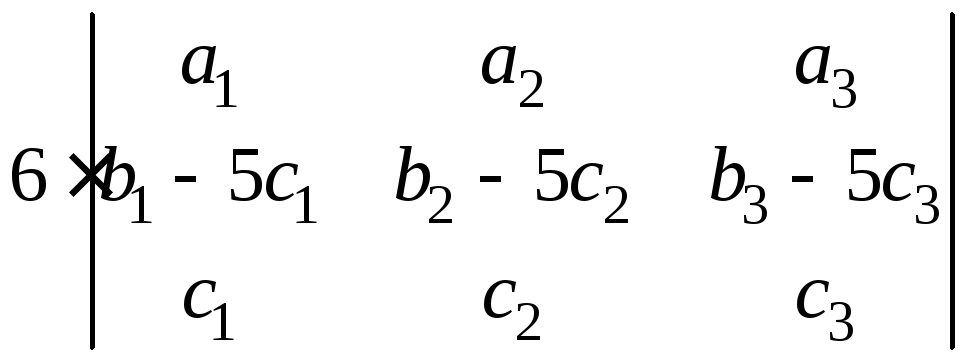 =
=
=
–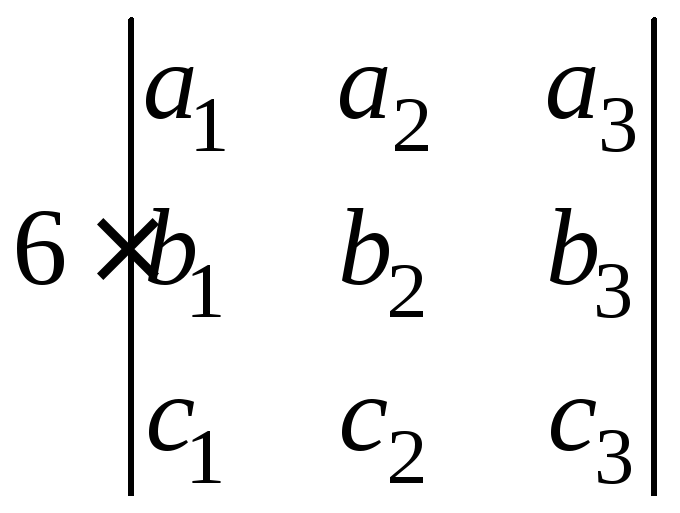 –
–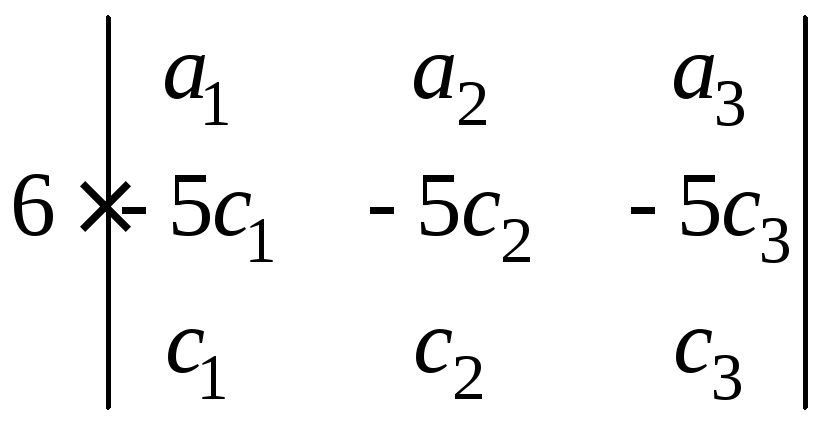 =
=![]() – 6·0 =
– 6·0 =![]() .
.
Дії 1) і 2) не змінили визначник. Після перетворення 3) визначник змінив знак, а доданок

дорівнює нулю, оскільки в ньому другий та третій рядки пропорційні.
Приклад 2.7. Як зміниться визначник шостого порядку, якщо в ньому поміняти місцями третій та четвертий стовпці, а потім від другого рядка визначника відняти п’ятий рядок?
Розв’язання. Після перестановки місцями третього та четвертого стовпців за властивістю 3 визначник змінить знак. Коли від другого рядка відняти п’ятий рядок, то за властивістю 9 визначник не зміниться. Отже, після вказаних дій визначник змінить знак.
Приклад 2.8. Як зміниться визначник п’ятого порядку, якщо всі елементи його першого рядка поділити на 2, а потім у всіх елементів визначника змінити знак?
Розв’язання.
Якщо
всі елементи першого рядка визначника
поділити на
2,
то визначник також поділиться на 2
(властивість 5). Зміну знаків у всіх
елементів визначника ми отримаємо, якщо
помножимо всі елементи кожного рядка
визначника на (–1). У результаті визначник
помножиться на (–1)5
= –1. Отже, після виконання вказаних дій
визначник помножиться на
![]() .
.
Приклад 2.9. Як зміниться визначник n-го порядку (n 3), якщо до його другого стовпця, помноженого на 3, додати останній стовпець, помножений на 5?
Розв’язання. Коли ми до другого стовпця визначника, помноженого на 3, додаємо останній стовпець, помножений на 5, то ми спочатку елементи другого стовпця множимо на 3, в результаті чого визначник множиться на 3, а потім до зміненого другого стовпця додаємо останній стовпець, помножений на 5, після чого визначник вже не змінюється. Отже, в результаті вказаних дій визначник помножиться на 3.
Приклад 2.10. Як зміниться визначник четвертого порядку, якщо стовпці визначника записати в оберненому порядку?
Розв’язання. Якщо ми переставимо місцями перший та четвертий стовпці визначника, а потім – другий та третій, то стовпці визначника будуть розташовані в оберненому порядку. Від однієї перестановки стовпців визначник змінює знак, після двох перестановок знак не зміниться. Тобто визначник четвертого порядку не зміниться, якщо його стовпці записати в оберненому порядку.
Задача 2.11. Користуючись властивостями визначників, довести, що подані визначники дорівнюють нулю, не розгортаючи їх.
а)
 ;б)
;б)
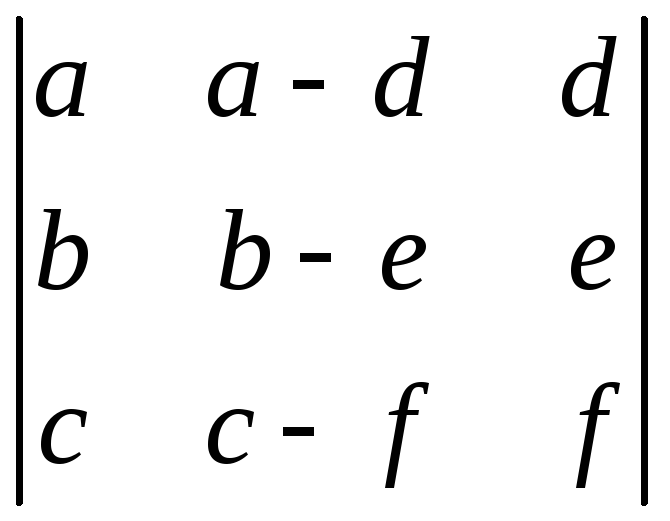 ;в)
;в)
 ;г)
;г)
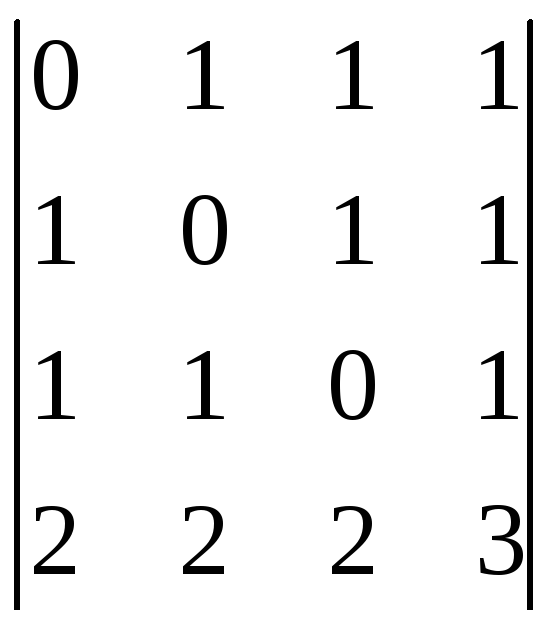 ;
;
д)
 ;е)
;е)
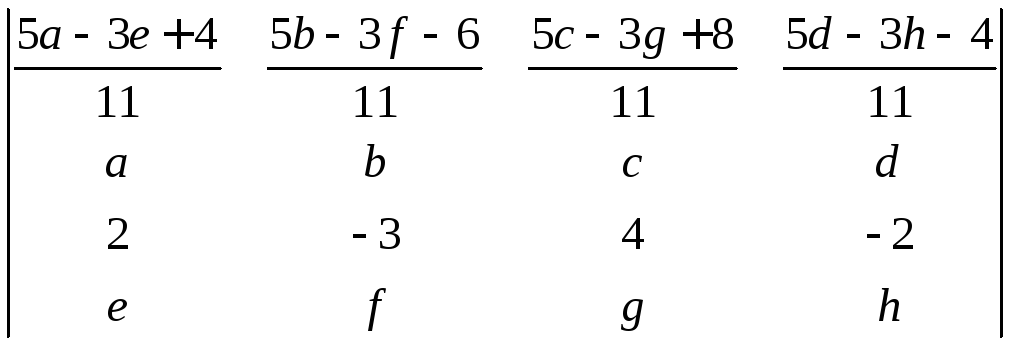 .
.
Задача 2.12. Як зміниться визначник четвертого порядку, якщо від його другого рядка відняти четвертий рядок?
Задача 2.13. Як зміниться визначник десятого порядку, якщо в ньому поміняти місцями перший та останній стовпці, а потім у всіх елементів визначника змінити знак?
Задача 2.14. Як зміниться визначник шостого порядку, якщо до його першого стовпця, помноженого на 2, додати шостий стовпець, потім помножити на (–16) всі елементи п’ятого стовпця, а після цього всі елементи визначника поділити на 2?
Задача 2.15. Як зміниться визначник n-го порядку, якщо у всіх його елементів змінити знак?
Задача 2.16. Як зміниться визначник сьомого порядку, якщо його стовпці записати в оберненому порядку?
Задача 2.17. Як зміниться визначник n-го порядку (n 2), якщо до його останнього рядка, помноженого на 3, додати суму всіх інших рядків?
Задача
2.18.
Відомо, що
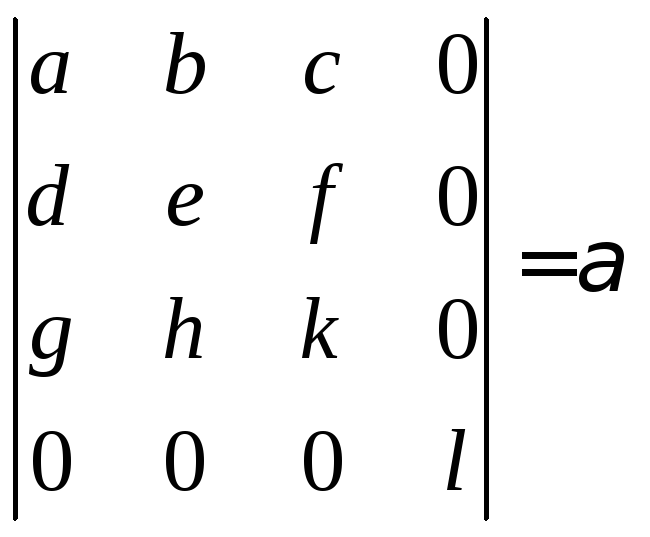 .
Знайти подані визначники:
.
Знайти подані визначники:
а)
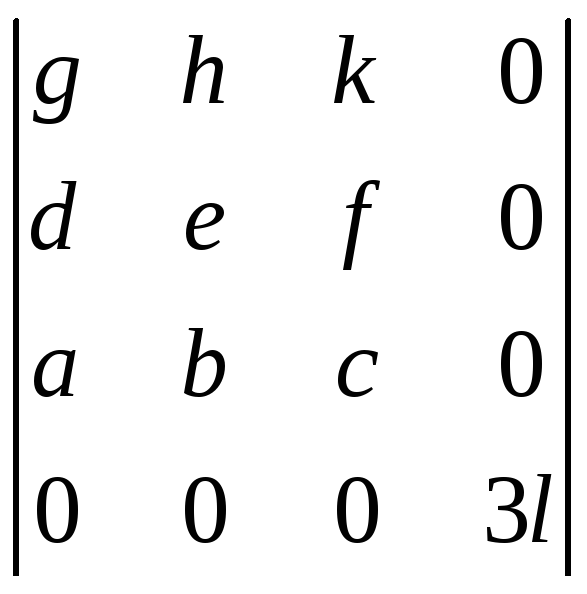 ;б)
;б)
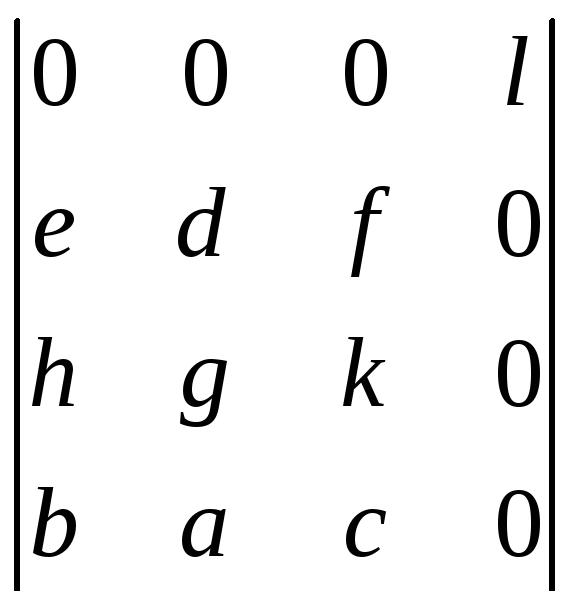 ;в)
;в)
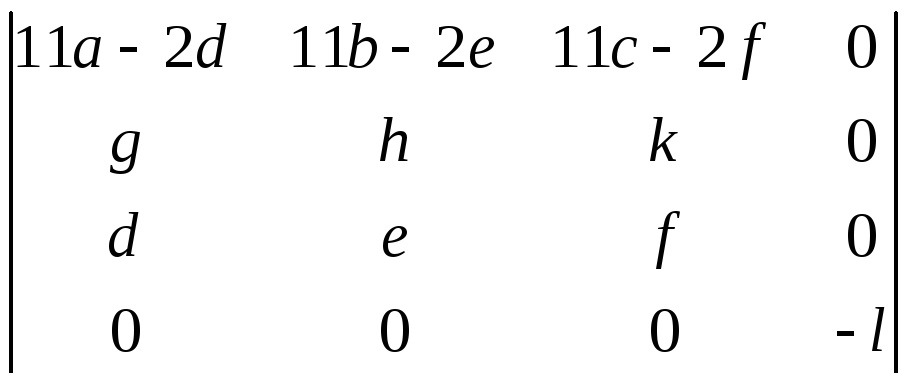 .
.
Задача
2.19.
Обчислити визначник
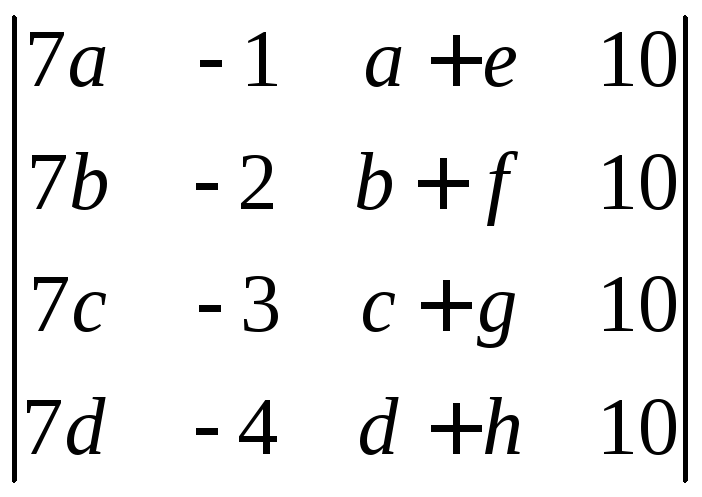 ,
якщо відомо, що
,
якщо відомо, що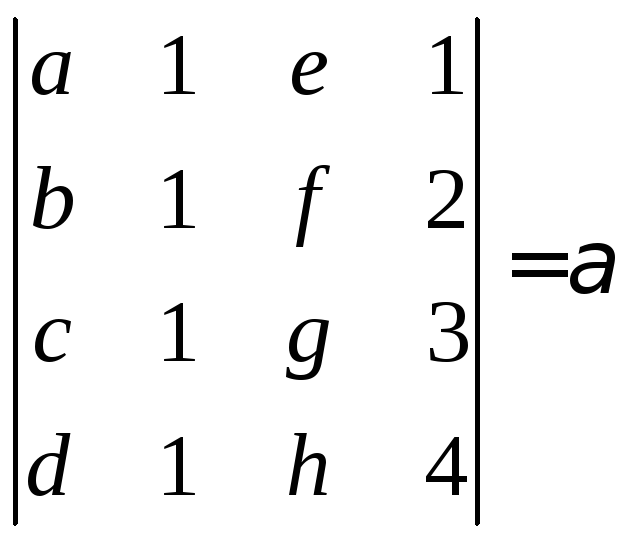 .
.
Задача
2.20.
Визначник матриці
![]() називається кососиметричним,
якщо
називається кососиметричним,
якщо
![]() для всіхi,
j,
1
i,
j
n.
Довести, що кососиметричний визначник
непарного порядку дорівнює нулю.
для всіхi,
j,
1
i,
j
n.
Довести, що кососиметричний визначник
непарного порядку дорівнює нулю.
