ВЫШМАТ

Комментарий

•Таким образом, не обращение в нуль определителя Вронского хотя бы в одной точке рассматриваемого интервала является достаточным условием для линейной независимости функций. В случае , когда функции являются решениями линейного однородного д.у. необходимым является более сильное условие. А именно, справедлива следующая теорема:

40

Признак линейной независимости решений линейных однородных д.у.

• Теорема 3. Если функции	y (x),..., y (x), x (a,b)
	1	m
линейно независимы и являются решениями
линейного однородного д.у. (3) с непрерывными
коэффициентами на (a,b)	, то определитель
Вронского отличен от нуля во всех точках
рассматриваемого промежутка		(a,b) .

41

Комментарии к теореме 3

•	Пример. Рассмотрим функции вида
			1)	3	, x (0; 1]
		(x
	y1(x)				,
		0,	x (1; 2)
			0, x (0; 1)
					.
	y (x)
	2	(x 1)3 , x [1; 2)
•	Функции линейно независимы для x (0; 2) .
	Определитель Вронского		W (x) 0 равен нулю для всех
	x (0; 2)

42

Продолжение примера

•Обе функции являются решением дифференциального уравнения

				6
	y			(x 1)2 y 0

• Но по теореме 3

W (x) 0, x (0;2)

• Вопрос. Почему получено противоречие теореме 3?

43

• Определение. Система n линейно независимых

решений

y1(x),..., yn(x) , x (a,b)

линейного однородного д.у. порядка n (число решений совпадает с порядком д.у.) называется

фундаментальной системой решений.
Пример. Система функций ex , e x	является

фундаментальной системой решений уравнения

y y 0.

44

Структура общего решения линейного однородного д.у.

• Теорема 4. Если функции

y1(x),..., yn(x) , x (a,b)

образуют фундаментальную систему решений линейного однородного д.у. порядка n с непрерывными на (a,b) коэффициентами, то общее решение уравнения в области

x (a,b), y ( , ),..., y(n1) ( , ).

имеет вид
y C1 y (x) ... Cn yn(x),	x (a,b)
1

45

2.3 Решение однородных ЛДУ порядка n с постоянными коэффициентами

Однородные ЛДУ порядка n с постоянными коэффициентами записываются следующим образом:

(2.6)

где ai – вещественные константы.

Задача построения общего решения (2.6) будет решена, если будет найдена фундаментальная система решений.

2.3.1 Случай действительных различных корней характеристического уравнения

Для уравнения первого порядка

,

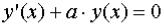решение запишется в виде

Эйлер предложил и решение уравнения (2.6) искать в таком же виде, т.е. 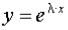. Если данная функция - решение (2.6), то она должна обращать это уравнение в тождество:

где

– характеристический полином, который легко получить из однородного ЛДУ, заменив производные от y(x) на 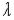в соответствующей степени. При коэффициенте .

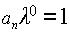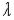Ясно, что - решение для тех , которые обращают 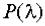в нуль.

Тогда	– характеристическое уравнение. Его корни	– характеристические
числа однородного уравнения.
Пусть все	- различные и вещественные числа. Подставив	в функцию
, найдём n вещественных частных решений (2.6):

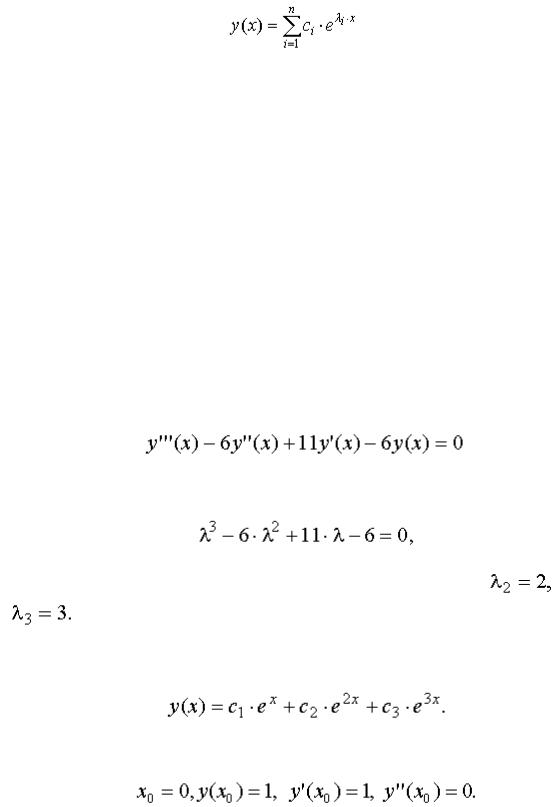
Эти решения - линейно независимые (их вронскиан не равен нулю для всех x), т.е.

составляют фундаментальную систему решений (ФСР).

Тогда согласно (2.4)

есть общее решение линейного однородного уравнения порядка n с постоянными коэффициентами (2.6), где:

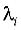– характеристические числа;

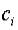– произвольные коэффициенты;

n – порядок уравнения (порядок старшей производной);

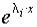– фундаментальная система решений.

Задача Коши для заданных числовых значений 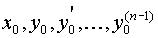приводит к решению системы алгебраических уравнений (2.5) относительно ci.

Пример. Дано дифференциальное уравнение

.

Характеристический полином запишется в виде

а характеристические числа (корни данного полинома) будут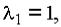

Тогда ex, e2x, e3x - ФСР, а общим решением будет функция

Решим задачу Коши для начальных условий:

Запишем по (2.5) систему уравнений для заданных начальных условий:

После подстановки численных значений начальных условий получим систему алгебраических уравнений по отношению к ci:

Решив последнюю систему, получим: c1=0.5, c2=1, c3= -0.5, и решение в форме Коши будет иметь вид

2.3.2 Случай различных корней характеристического уравнения, среди которых есть комплексные

Пусть среди корней характеристического полинома 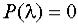есть некоторый комплексный корень:

где a и b– числа, .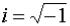

Так как все коэффициенты полинома вещественные, тогда есть и сопряжённый ему корень

.

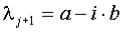Таким образом, решение для корня будет комплексным.

В разделе 2.1 показано, что каждая комплексная функция, являющаяся решением ЛДУ, порождает два вещественных решения, причём линейно

независимых 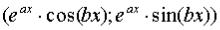, т.е. входящих в фундаментальную систему решений:

Для сопряжённого корня 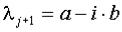решениями будут:

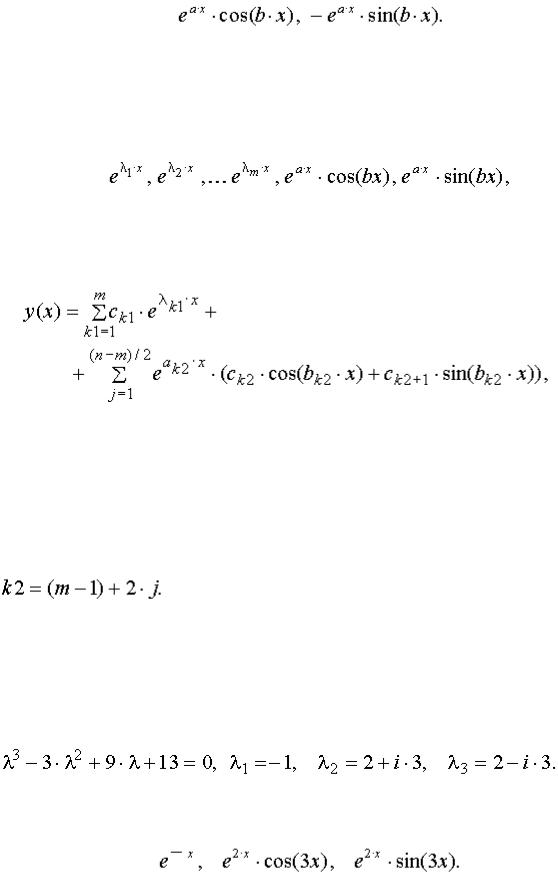
При этом первые решения совпадают, а вторые - линейно зависимы. Таким образом,

сопряжённый корень не порождает новых вещественных, линейно независимых решений, и соответствующие ему функции не включаются в ФСР.

Всего получим n решений вида:

образующих фундаментальную систему решений.

Для этого случая общее решение запишется в виде

(2.7)

где m – число корней действительных разных; n – порядок дифференциального уравнения;

j = 1, ..., (n-m)/2;

(n-m) – число комплексных и сопряжённых корней;

Пример. Построим общее решение уравнения

.

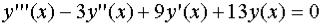Найдем характеристическое уравнение и его корни:

Фундаментальной системой решений для найденных 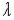будут функции:

Тогда общим решением заданного однородного уравнения с постоянными коэффициентами будет функция