1.3. Представление периодических сигналов тригонометрическим рядом Фурье

Оценку качества прохождения сложного сигнала s(t) в электронной цепи, в том числе и импульсной формы, часто бывает удобно проводить, предварительно представив его в форме гармонического ряда Фурье:

(1.4)

или

, (1.5)

где – низшая граничная частота в спектре периодического сигнала;

–постоянная составляющая функции; (1.6)

–амплитуда косинусной составляющей (1.7)

–амплитуда синусной составляющей (1.8).

Пределы интегрирования t₁,t₂определяют временную область, в пределах которой задается функцияs(t).

По известным значениям амплитуд a_k,b_kрассчитываются полная амплитудаk-й гармоники и ее фаза:

, . (1.9)

Тригонометрический ряд Фурье можно записать в комплексной форме, воспользовавшись формулой Эйлера:

, (1.10)

где 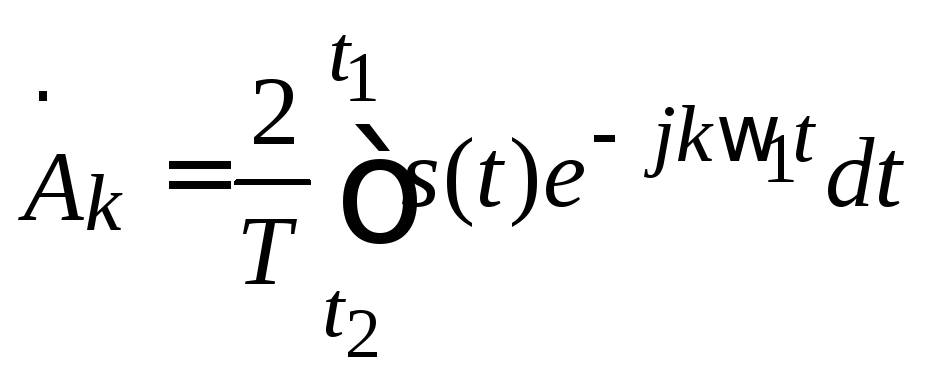(1.11)

– комплексная амплитуда k-й гармоники.

Комментируя приведенные выше соотношения, отметим следующее. Сложный периодический сигнал может быть представлен в виде суммы гармонических составляющих, частоты которых кратны основной частоте , а амплитудный и фазовый спектры являются линейчатыми. Постоянную же составляющую следует рассматривать как гармонику нулевой частоты, значение которой равно среднему значению функции за период.

1.4. Спектральное представление непериодических сигналов

Рассмотренные выше представления аналоговых сигналов в виде тригонометрического ряда Фурье относятся только к периодическим функциям. В случае непериодических сигналов используется интегральная форма преобразования Фурье, с помощью которой одиночный сигнал (cпериодомТ =) представляется в виде:

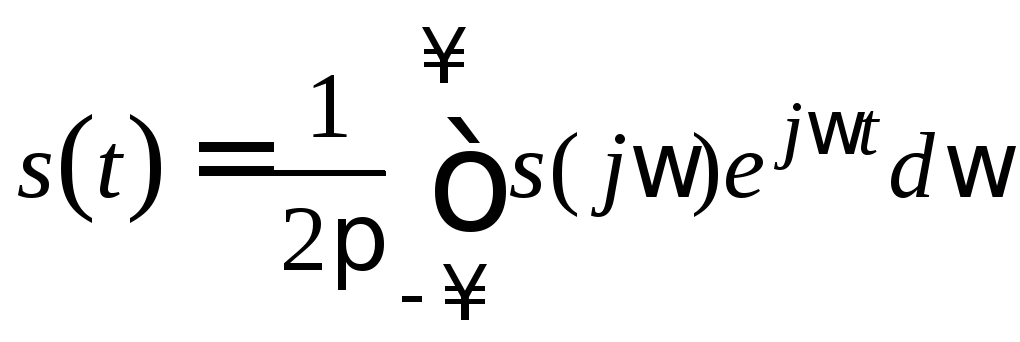(1.12)

– обратное преобразование Фурье,

где s(j) – спектральная плотность сигнала, определяемая соотношением:

(1.13)

– прямое преобразование Фурье.

Физический смысл функции спектральной плотности заключается в том, что она устанавливает связь между комплексной амплитудой некоторого эквивалентного гармонического сигнала, отражающего вклад всех спектральных компонентов, находящихся в бесконечно малой полосе частот = 2/Т, и значением этой полосы:

. (1.14)

В отличие от спектра периодической функции, носящим дискретный характер, спектр непериодической функции непрерывен.

Как следует из (1.13), спектральная плотность содержит действительную и мнимую части, что дает право утверждать, что в ней есть информация и об амплитудном спектре сигнала, и фазовом спектре.

Рассмотрим примеры расчета параметров тригонометрического ряда Фурье и функции спектральной плотности.

Пример 1. Рассчитать коэффициенты ряда Фурье для сигналаs(t), изображенного на рис. 1.1,ди представляющего собой периодическую последовательность прямоугольных импульсов с амплитудойА, длительностью импульсаt_ии периодом повторенияТ.

На основании формул (1.6) – (1.8) получим:

1. Постоянная составляющая

. (1.15)

2. Амплитуда косинусной составляющей

. (1.16)

3. Амплитуда синусной составляющей

. (1.17)

Из формул (1.16), (1.17) находим амплитуду k-й гармоники и ее фазу:

(1.18)

Пример 2. Определить функцию спектральной плотности сигнала, представляющего одиночный импульс конечной длительностиt_ии амплитудойА(рис. 1.1,в).

По формуле (1.13) находим:

. (1.19)

Выделив действительную и мнимую части выражения (1.19), найдем модуль спектральной плотности и ее фазу:

. (1.20)

Спектральная плотность имеет максимум при = 0 и обращается в нуль при значениях частоты:

, где n = 1, 2, …, (1.21)

т. е. эти гармоники в спектре одиночного импульса отсутствуют.

Сопоставляя (1.18) и (1.20), нетрудно увидеть их сходство. Принципиальное же отличие состоит в том, что и модуль, и фаза спектральной плотности являются непрерывными функциями частоты, их можно рассматривать в качестве огибающих для амплитудного и фазового спектра аналогичных по форме функций с конечным периодом.