Как понимать квантовую механику

6.3. ОДНОМЕРНАЯ ЗАДАЧА РАССЕЯНИЯ

183

Чтобы исследовать зависимость решений, используем вронскиан (6.12) (см. 6.2.3 «Вронскиан (л*)»). Для частиц, движущихся с одинаковой энергией в одинаковых потенциалах, вронскиан от координаты не зависит (6.13)!

Подставляя в вронскиан асимптотики на ±∞ четырех¨ связанных с одномерной задачей рассеяния решений уравнения Шредингера¨ ψ(x), ψ (x), ψo(x), ψo (x), мы получим ряд тождеств на параметры этих асимпто-

тик r, d, ro, do, k, k .
•	i	W [ψ, ψ ] = k |d|2	= k(1 − |r|2) — с точностью до множителя этот
	2
		x→+∞		x→−∞

вронскиан совпадает с током вероятности j для решения ψ(x). Мы еще¨ раз доказали сохранение вероятности в одномерной задаче рассеяния.

• 2

o

o

−

− |

o|

− | o|

i

W [ψ

, ψ ] =

k (1

r

2) =

k d

2 — с точностью до множителя

этот вронскиан

j

ψo(x)

x→+∞

x→−∞

.

совпадает с током вероятности для решения

•

i

W [ψ, ψo] =

k d

=

kdo

— отсюда получаем (поскольку k и k

2

вещественны),

x→+∞

x

что

→−∞

k

2

=

k

2

= Do.

D = k |d|

|do|

k

Коэффициенты прохождения (а значит и коэффициенты отражения) через барьер в обе стороны одинаковы!

• i W [ψ, ψ ] = k dr

2 o o

x→+∞

=−kd r.

o

x→−∞

6.3.6. Волновые пакеты

До сих пор мы рассматривали рассеяние на потенциале бесконечно длинных монохроматических волн. Это предельный случай, который принципиально не может быть реализован на практике, т. к. плоская волна, как и любое состояние непрерывного спектра, не может быть нормирована на единицу.

Реальное рассеяние — рассеяние волновых пакетов, которые уже не являются монохроматическими, но зато имеют конечную норму. Рассеяние достаточно длинных волновых пакетов (длинных по координате и узких по

184

ГЛАВА 6

импульсу) должно в пределе соответствовать тому, что мы уже получили для монохроматических волн (состояний с определенной¨ энергией).

Следует ожидать, что падающий волновой пакет, провзаимодействовав с потенциалом, расщепится на два волновых пакета: прошедший и отраженный,¨ причем¨ интегралы от |ψ(x)|2 по интервалам, содержащим, соответствующие пакеты будут соответствовать коэффициентам прохождения и отражения для данного потенциала.

Свободный волновой пакет

Рассмотрим волновой пакет, распространяющийся в потенциале U (x) = = const. Полученный результат потом можно будет сравнить с асимптотическим поведением отраженной¨ и прошедшей волн в областях x → ±∞, где потенциал выходит на константу.

Мы уже рассматривали движение и расплывание волнового пакета ранее (5.2.6 «Эволюция волнового пакета для свободной частицы»).

Любую волновую функцию можно разложить по монохроматическим

волнам, используя преобразование Фурье:

ψ(x) =	1			eikx f (k − k0) dk.	(6.21)
	√
		2π

Волновой пакет, который нас интересует, должен описываться функцией f (k − k0), которая быстро стремится к нулю, когда k удаляется от k0, тогда волна будет близкой к монохроматической.

Вынеся из под интеграла множитель eik0x, мы записываем ψ(x) в виде произведения монохроматической волны на медленно зависящую от ко-

˜

ординаты амплитуду f (x), связанную с функцией f (k ) преобразованием Фурье:

ψ(x) = e

ik

x

1

ik x

f (k ) dk

= f˜(x) e

ik

x

(6.22)

0

e

0

.

√

2π

˜

f (x)

, на котором спадает функция

,

Характерное изменение

волнового числа

δk

f

должно быть достаточно малым по сравнению с k0.

Волновая функция ψ(x) осциллирует с волновым числом, близким к k0, при этом длина волнового пакета δx δk1 оценивается из соотношения неопределенностей¨.

Волна с волновым числом k осциллирует во времени с циклической частотой ω(k):

ei(kx−ω(k) t).

6.3. ОДНОМЕРНАЯ ЗАДАЧА РАССЕЯНИЯ

185

В частности, для свободной нерелятивистской частицы

ω(k) =

E(k)

=

¯hk

2

.

¯h

2m

Для исходного волнового пакета получаем

ψ(x, t) = √2π e

−

f (k − k0) dk =

1

i(kx ω(k) t)

= e

i(k x ω(k

) t) 1

i(k x [ω(k

+k )

ω(k

)] t)

0 −

0

e

−

0

−

0

√

2π

(6.23)

f (k ) dk .

Предположим, что функция f (k ) достаточно быстро спадает с ростом аргумента, чтобы разность частот можно было выразить через производ-

ную:	k0
dω
ω(k0 + k ) − ω(k0) ≈ dk		k = v(k0) k .
ω0

Здесь v0 = v(k0) = dωdk k0 — функция с размерностью скорости, которую далее мы идентифицируем как групповую скорость (для свободной частицы

v(k) = ¯hk =

p

)

m

m

ψ(x, t) ≈ e

i(k x ω

t)

1

e

ik (x v t)

f (k ) dk =

0 −

0

− 0

√

2π

= f˜(x

0

v t) e

0x−

t).

˜

f (x−v0 t)

− 0

i(k

ω

Таким образом, волновой пакет движется, не меняя формы10, с повой скоростью v0 = v(k0).

(6.24)

груп-

Рассеяние волнового пакета*

Точно также как выше (6.21), мы построили волновой пакет из монохроматических волн, построим с помощью той же функции f (k − k0) суперпозицию волновых функций, описывающих рассеяние почти моно-

10Чтобы учесть расплывание волнового пакета, разность частот ω(k0 + k ) − ω(k0) надо разложить до второй производной по k , чтобы учесть дисперсию (зависимость от волнового числа) групповой скорости.

186

ГЛАВА 6

хроматических волн:

ψ(x) =

1

ψk(x) f (k − k0) dk,

√

2π

ψ (x) +

2m

(E(k)

−

U (x))ψ

(x) = 0,

k

¯h2

k

ψk(x) → eikx + r(k) e−ikx, x → −∞,

ψk(x) → d(k) eik (k)x, x → +∞,

¯h2k2

1

E(k) =

2m , k (k) =

¯h 2m(E(k) − U+) =

dk =

˜

dx = 1.

|f (k)|

2

2

|f (x)|

(6.25)

'

k2 − 2mU+ ,

¯h2

Если теперь учесть зависимость от времени, дающую для состояния

с энергией E(k) множитель e−iω(k) t, ω(k) =					E(k)		, мы получим
						¯h
ψ(x, t) = √2π
			ψk(x) e−	iω(k) t		f (k − k0) dk.		(6.26)
1

Исследуем асимптотическое поведение ψ(x, t) при x → ±∞. Запишем амплитуды отражения и прохождения в следующем виде:

r(k) = |r(k)| eiα(k) ≈ |r(k)| ei(α0+α1 (k−k0)) ≈ r0 eiα1(k−k0), d(k) = |d(k)| eiβ(k) ≈ |d(k)| ei(β0+β1(k−k0)) ≈ d0 eiβ1(k−k0).

Мы пренебрегли изменением абсолютной величины амплитуд, но учли изменение их фазы до первого порядка по k − k0.11

Проделывая для двух слагаемых асимптотики x → −∞ преобразования, аналогичные преобразованиям, приведшим к бегущему волновому пакету (6.24), получаем

x → ∞,

(6.27)

ψ(x, t) → √2π

(e

ikx

+ r(k) e−

ikx

) e−

iω(k) t

f (k − k0) dk =

1

11

Если учесть зависимость |r|

и

|d| от k, то это

приведет¨ лишь к

2

искажению формы волно-

вого пакета и необходимости усреднения R(k) и D(k) с весом |f (k − k0)| .

6.3. ОДНОМЕРНАЯ ЗАДАЧА РАССЕЯНИЯ

187

1

i(kx ω(k) t)

=

e

−

f (k − k0) dk +

√

2π

1

i(

kx ω(k) t+α (k

k

))

+

r0 e

− −

1

− 0

f (k − k0) dk =

√

2π

= f˜(x − v0 t) ei(k0x−ω0t) + r0f˜(α1 − x − v0 t) ei(−k0x−ω0t) .

падающий пакет

отраженный¨ пакет

, когда

Мы видим, что при достаточно больших отрицательных значениях

x

потенциал уже можно считать константой, падающий волновой пакет, чья

˜ −

форма описывается функцией f (x v0 t), движется направо по закону x = = v0 t. Через рассматриваемую область этот пакет проходит при больших отрицательных временах.

Вероятность обнаружить частицу в падающем пакете равна 1:

0	|ψ(x, t → −∞)|2 dx =		|ψ(x, t)|2 dx = |f˜(x)|2 dx = 1.
−∞
Отраженный¨			˜
		пакет имеет форму, описывающуюся функцией f (−x −

−v0 t + α1), он движется через ту же область больших отрицательных x по закону

α1

x = α1 − v0 t = −v0 t −

.

v0

2

Вероятность обнаружить частицу в отраженном¨

пакете равна |r0| , т. е.

коэффициенту (вероятности) отражения:

0

|ψ(x, t → +∞)|2 dx = |r0f˜(−x)|2 dx =

−∞

= |r0|2

|f (k − k0)|2 dk = |r02| = R0.

Функцию k (k) мы также разложим до первого порядка по k − k0:

k (k) = k (k0) + dk k=k0

(k − k0) = k1 + Ck2,

dk

C

dk

k

k0

k1

k2

C = dk

k=k0

=

k

k=k0

=

k1

.

188 ГЛАВА 6

Проделывая для x → +∞ аналогичные преобразования, получаем

x → +∞,

1

ik (k) x

(6.28)

ψ(x, t) →

e−

iω(k) t

f (k − k0) dk ≈

d(k) e

√

2π

f (k − k0) dk ≈

≈ e

1 −

0

t)

√2π

d0 e

− 0

−

− 0

1

− 0

))

i(k x ω

1

i(C(k

k

) x [ω(k)

ω

] t+β (k

k

≈ e

1 −

0

t)

√2π

d0 e

2

−

0

1

f (k2) dk2 =

i(k x ω

1

ik

(C x v(k

) t+β )

= d

0

f˜(Cx

−

v(k

) t + β

) ei(k1x−ω0t)

=

0

1

= d0

v1 =

˜ k0 f

k1

v(k0)

C

прошедшая волна
(x − v1t) + β1 ei(k1x−ω0t),
	dω
=	dk		=	dω		.	(6.29)
	dk			dk
					k =k1
	dk
		k =k1

Таким

образом,

прошедший

пакет имеет форму, описывающуюся

˜

k0

(x

v1t) + β1 , которая сжата по координате, по сравне-

функцией f

k1

нию с функцией

f˜,−в

k0

раз, он движется через область больших положи-

тельных x по закону

k1

k1

β1k1

β1

x = v1 t − β1

= v1

t −

= v1

t −

.

k0

v1k0

v0

Вероятность обнаружить частицу в прошедшем пакете равна |d|2 k1 ,

т. е. коэффициенту (вероятности) прохождения:

k0

	|ψ(x, t → +∞)|2 dx = d0 f˜	k1	x	dx = |d0|2	k0	= D0.
+∞				2
0		k0			k1

Таким образом, мы проверили, что определенные¨ ранее коэффициенты отражения и прохождения действительно определяют вероятности отражения и прохождения частицы для почти монохроматического волнового пакета.

6.3. ОДНОМЕРНАЯ ЗАДАЧА РАССЕЯНИЯ

189

Если продолжить законы движения волновых пакетов на малые времена, то окажется, что через точку x = 0 они проходят в ненулевые моменты

времени, α1 и β1 .

v0 v0

Если α1(v0 − v1) + 2v1β1 = 0, тогда три прямые, изображающие движение трех¨ волновых пакетов, пересекаются в одной точке и мы можем обратить эти задержки в нуль сдвигом начала координат по x, но в общем случае эти задержки не могут быть обнулены.

Таким образом, рассмотрев рассеяние волновых пакетов, мы не только проверили постановку одномерной задачи рассеяния, но и уточнили ее¨. Теперь помимо амплитуд и коэффициентов отражения и прохождения мы можем определять времена (или длины) задержки волновых пакетов при рассеянии. Длины задержки можно выразить следующими формулами

α1

(k) = Im

1

d

r(k),

β1

(k) = Im

1

d

d(k).

r (k) dk

d (k) dk

Соответствующие времена получаются делением на групповую скорость

при x → −∞, т. е. v0 = ¯hkm .

Далее мы рассмотрим эти задержки на примерах рассеяния на ступеньке и δ-яме.

Пример: задержка волновых пакетов, рассеянных ступенькой*

Вернемся¨ к рассмотренному ранее процессу рассеяния волнового пакета на ступеньке. Амплитуды прохождения и отражения имеют вид (6.17)

	d =	2k	,	r = k − k	,	E > V, k, k		R.
		k + k
				k + k

Для энергии выше высоты ступеньки обе амплитуды вещественны, т. е. прошедший и отраженный¨ волновые пакеты выходят из начала координат без задержки.

Для энергии ниже высоты ступеньки d надо положить равным нулю, а амплитуды r можно получить аналитическим продолжением:

			d = 0,
		1 √			1
	k =		2mE, κ =
		¯h			¯h

r =		k − k	= k − iκ , E < V, k, κ							R,
		k + k		k + iκ
					2mV
						− k2	2		− k2,
2m(V − E) = ' ¯h2							= (κ1

190 ГЛАВА 6

k − i κ12

k2

1

2

2mV

r(k) =

k + i

−

,

r = r

,

κ1

=

¯h2

,

κ2

k2

1

−

4

2

2

− 4k

4

α1

(k) = Im

1

dr = Im r dr

= 2

κ1

+ 4κ1k

.

κ14κ

r dk

dk

50

40

30

20

10

0

0

0.2

0.4

0.6

0.8

1

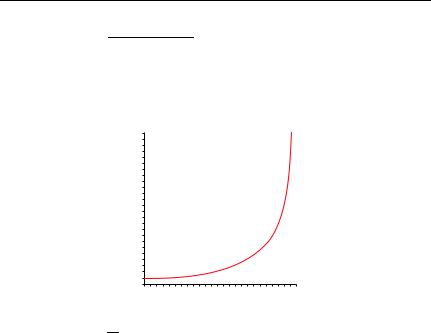
Рис. 6.6. α1(k) — длина задержки для волны, отраженной¨ от ступеньки. Единица

измерения длины — 1 .

κ1

Для высокой ступеньки (κ1 k) получаем

α1(k) ≈ κ2 .

То есть задержка отраженного¨ волнового пакета соответствует глубине проникновения волны в потенциальный барьер.

Пример: задержка волновых пакетов, рассеянных δ-ямой*

Вернемся¨ к рассмотренному ранее процессу рассеяния волнового пакета на δ-яме. Амплитуды прохождения и отражения имеют вид (6.18)

d =		k			r =	iκ0
				,				.
		k − iκ0				k − iκ0
α1 = κ0	κ02 − 3k2				β1 = −κ0		k2 − 3κ02
	(k2 + κ02)2		,				(k2 + κ02)2		.

6.3. ОДНОМЕРНАЯ ЗАДАЧА РАССЕЯНИЯ

191

3
2.5
2
1.5
1
0.5
0
0	1	2	3	4	5

k

Рис. 6.7. Длина задержки для волны, отраженной¨ (нижний график) и прошедшей

(верхний график) через δ-яму. Единица измерения длины — 1 .

κ0

В пределе низкой энергии (|κ0| k) задержки определяются длиной затухания волновой функции в связанном состоянии δ-ямы:

α1 ≈	1	,	β1 ≈	3	.
	κ0			κ0

В пределе высокой энергии (|κ0| k) мы получаем уже не задержки, а опережения:

α1 ≈ −3	κ0		β1 ≈ −	κ0
		,			.
	k2			k2

6.3.7. Резонансное рассеяние*

Процесс рассеяния на потенциале можно рассматривать как интерференцию падающей волны и волн, отраженных¨ (возможно многократно) от неоднородностей потенциала. При этом в зависимости от соотношения длин волн и расстояний между неоднородностями (характерных длин потенциала) интерференция может усиливать или ослаблять отраженную¨ или прошедшую волну. В результате коэффициенты отражения и прохождения могут осциллировать при изменении энергии (и волнового числа) падающей волны.

Проще всего анализировать подобную ситуацию для случая кусочнопостоянного потенциала, когда все неоднородности являются точечными: представляют собой скачки потенциала.

Пусть при данной энергии E волновое число в области (x0, x0 + + a) длины a с локально постоянным потенциалом Ua составляет k = = ¯h1 2m(E − Ua). Решение стационарного уравнения Шредингера¨ в дан-

192

ГЛАВА 6

ной области записывается в виде

ψa(x) = A cos(kx) + B sin(kx).

Если в рассматриваемой области укладывается целое число волн, то вне зависимости от A и B значения волновой функции и ее¨ первой производной на концах интервала совпадают:

ka = 2πn, n

Z,

ψ

(x

) = ψ

(x

0

+ a),

ψ

(x

) = ψ

(x

0

+ a).

a

0

a

a

0

a

Если мы будем сшивать волновую функцию слева и справа от рассматриваемой области, то саму область (x0, x0 + a) можно удалить, напрямую склеив области (−∞, x0) и (x0 + a, +∞). Волновая функция вне вырезанного интервала при этом не изменится. В частности, не изменятся коэффициенты отражения и прохождения.

Если в рассматриваемой области укладывается полуцелое число волн, то вне зависимости от A и B значения волновой функции и ее¨ первой производной на концах интервала отличаются только знаком:

ka = π(2n+ 1), n		Z, ψ (x	) = ψ	(x	+ a), ψ (x	) = ψ (x	+ a).
		a 0	− a	0	a 0	− a 0

Если мы будем сшивать волновую функцию слева и справа от рассматриваемой области, то саму область (x0, x0 + a) можно удалить, напрямую склеив области (−∞, x0) и (x0 + a, +∞), поменяв при этом знак волновой функции в одной из этих областей. Волновая функция с одной стороны вырезанного интервала при этом не изменится, а с другой — поменяет знак. Коэффициенты отражения и прохождения снова не изменятся.

1
0.8
0.6
0.4
0.2
0
0	0.2	0.4	0.6	0.8	1

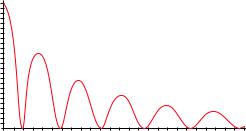
Рис. 6.8. R(E) для прямоугольной ямы при a = 30, ¯h = m = V = 1.

Таким образом, при рассмотрении одномерной задачи рассеяния в области постоянного потенциала можно убрать или добавить целое число полуволн без изменения коэффициентов отражения и прохождения.