Общая формулировка задачи линейного программирования

Примеры, рассмотренные выше, укладываются в общий класс задач линейного программирования. Однако запись линейной функции и, главным образом, ограничений в разных задачах заметно различается.

Ряд практических задач сводится к смешанным условиям: часть ограничений - линейные уравнения, другие - линейные неравенства. Такое разнообразие форм записи условий задач затрудняет создание и использование общих методов и вычислительных алгоритмов их решения. Поэтому естественно рассмотреть метод и алгоритм решения основной (стандартной) задачи линейного программирования и способы сведения любой задачи линейного программирования к основной форме, которая состоит в следующем. Задана система m линейных алгебраических уравнений с n неизвестными:

(7)

и линейная функция относительно переменных х₁, х₂, ¼, х_n:

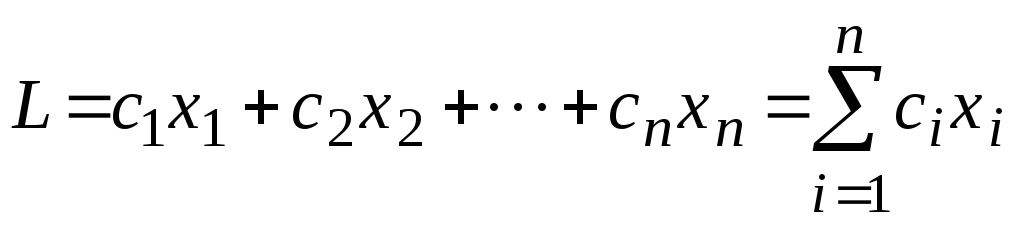(8)

Требуется найти такие неотрицательные значения переменных х₁, х₂, ¼, х_n, которые бы удовлетворяли системе линейных уравнений (7) и, кроме того, обращали в максимум линейную функцию (8).

Заметим, что если по условиям задачи требуется отыскать минимум функции L, записанной в виде (8), то задачу можно свести к задаче максимизации функции L¢, связанной с функцией L так:

L¢ = - L = -c₁x₁ - c₂x₂ - ¼ - c_nx_n. (9)

Максимум функции (9) и минимум функции (8) будут достигаться при одном и том же наборе переменных (х₁, х₂, ¼, х_n), удовлетворяющих условиям неотрицательности переменных и уравнениям (7), областью определения задачи.

Допустимым решением задачи линейного программирования будем называть любую совокупность переменных

х₁ ³ 0, х₂ ³ 0, ¼ , х_n ³ 0, (10)

удовлетворяющих уравнениям (7).

Оптимальным решением будем называть то из допустимых решений, для которого линейная форма L обращается в максимум (минимум).

Графический метод решения задачи линейного программирования

Если число неизвестных в задаче линейного программирования равно двум, т.е. n = 2, то ее можно решить графическим методом. Кроме того, графический метод дает геометрическую интерпретацию решения ЗЛП. В качестве примера рассмотрим частный случай задачи 1, когда комбинат выпускает 2 вида продукции, например, j = 1,2:

1. Булки

2. Пирожные.

Тогда система ограничений на ресурсы будет иметь следующий вид:

а₁₁х₁ + а₁₂х₂ £ b₁ - ограничение по муке

а₂₁х₁ + а₂₂х₂ £ b₂ - ограничение по сахару

а₃₁х₁ + а₃₂х₂ £ b₃ - ограничение по маслу

а₄₁х₁ + а₄₂х₂ £ b₄ - ограничение по творогу

а₅₁х₁ + а₅₂х₂ £ b₅ - ограничение по яйцам

Используя численные данные а_ij и b_i таблиц 3.2 и 3.3, получим следующую систему неравенств:

0,1×х₁ + 0,04×х₂ £ 200 (1)

0,01×х₁ + 0,05×х₂ £ 50 (2)

0×х₁ + 0,05×х₂ £ 50 (3)

0×х₁ + 0×х₂ £ 50 (4)

0,1×х₁ + 0,2×х₂ £ 500 (5)

Так как а₄₁ = 0 и а₄₂ = 0, то вместо пяти осталось четыре неравенства.

Превратим эти неравенства в равенства и построим в системе координат х₁, х₂ прямые (1), (2), (3), (5) ограничивающие область допустимых значений неизвестных х₁, х₂, представленную на рис.3.1.

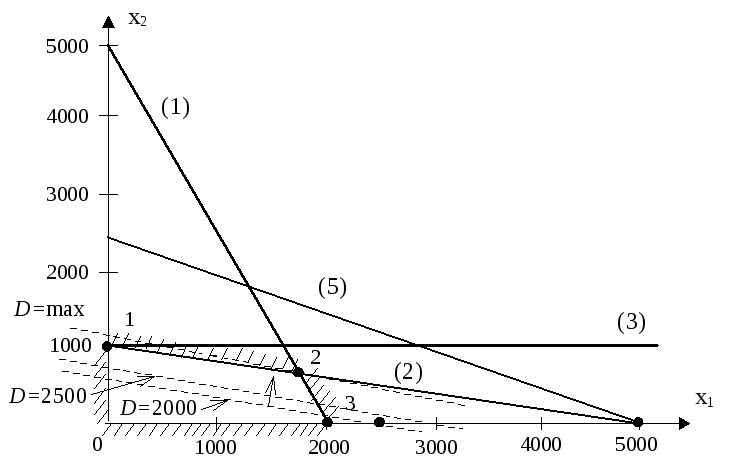
Рис. 1 Графическое решение ЗЛП при числе неизвестных n = 2

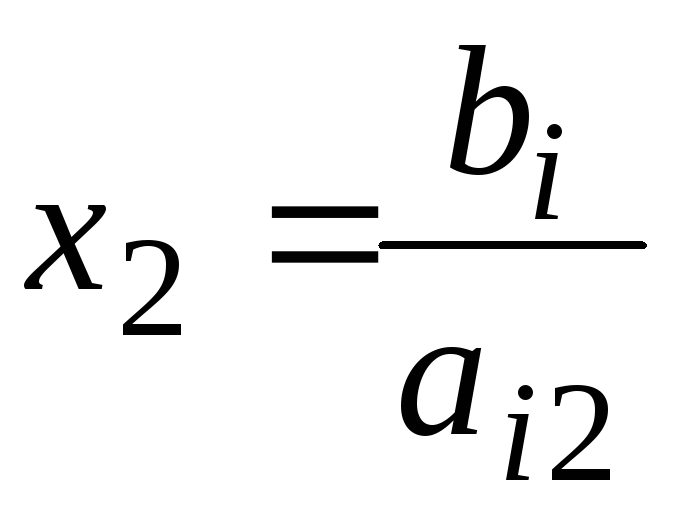Для построения прямых (1), (2), (3), (5) используется обычно такой прием. Сначала полагают х₁ = 0 и определяют на оси х₂. Затем полагают х₂ = 0 и определяют 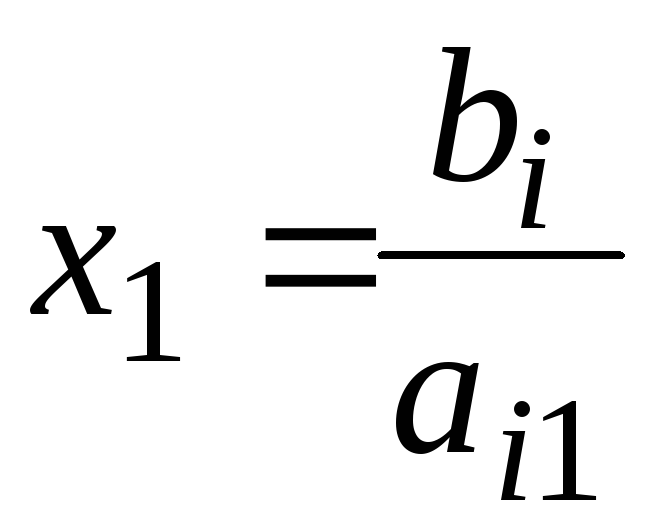на оси х₁. После этого через точки х₁ и х₂ на этих осях проводят прямые. Так для прямой (1) получим: х₁ = 0, , х₂ = 0, .

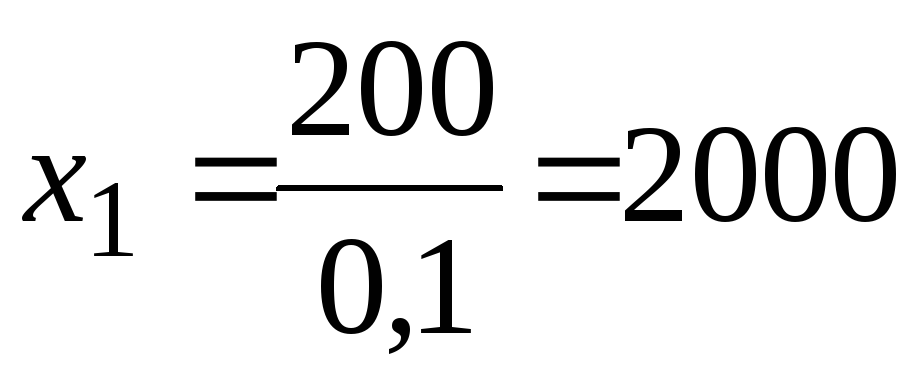Аналогично построим прямые (2) и (5). Прямая (3) идет параллельно оси х₁ со значением .

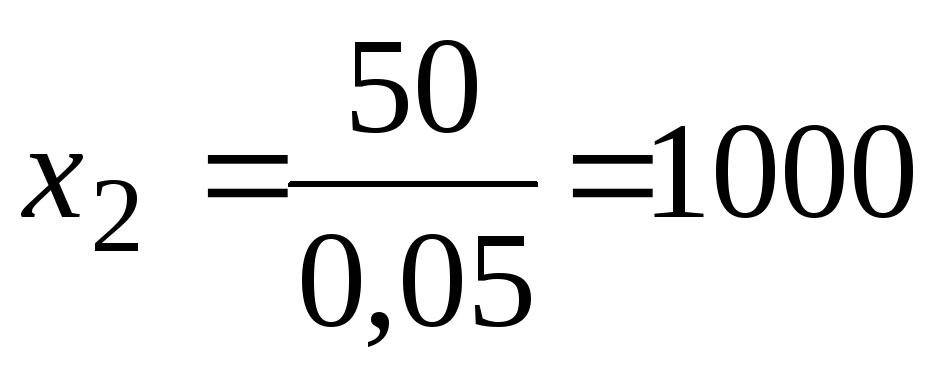Из рис.1 следует, что область допустимых значений х₁ и х₂ ограничена многоугольником с вершинами 0,1,2,3, образованного осями координат х₁ и х₂, а также прямыми (1) и (2), т.е. ресурсами мукой и сахаром. Прямые (3) и (5) в данном примере на область допустимых значений х₁ и х₂ не влияют.

Целевая функция в задаче 1 при двух видах продукции (булки и пирожное) примет вид

D = с₁х₁ + с₂х₂ = 0,84х₁ + 3,2х₂ = mах.

Для определения оптимальных значений х_1оп и х_2оп, при которых величина D= mах, используем следующий прием: зададим произвольно величину D > 0, например D = 2000, и построим прямую

0,84х₁ + 3,2х₂ = 2000.

Она пройдет через точки и на осях x₁ и x₂. На рис. 3.1 эта прямая показана пунктиром. Отметим, что прямая D = 2000 идет круче прямой (2). Если теперь увеличить значение D, например, D = 2500, тогда прямая D = 2500 переместится вверх параллельно прямой D = 2000. Увеличивая таким образом D, мы будем перемещать прямую параллельно самой себе до тех пор, пока она не достигнет верхней точки допустимой области. В данной задаче этой точкой является точка 2 пересечения прямых (1) и (2). Координаты этой точки определим, решив совместно систему из двух уравнений (1) и (2).

0,1×х₁ + 0,04×х₂ = 200 (1)

0,01×х₁ + 0,05×х₂ = 50 (2)

Решение этой системы таково

х_1оп = 1739, х_2оп = 652.

Доход фирмы при таком плане выпуска продукции (в точке 2) составит:

D₃ = с₁х_1оп + с₂х_2оп = 0,84×1739 + 3,2×652 = 1460,76 + 2086,4 = 3547,16 (руб).

При этом полностью будут израсходованы мука и сахар.

Отметим, что при других ценах с₁ и с₂ на продукцию фирмы прямая

D = с₁х₁ + с₂х₂

имела бы другой наклон, тогда оптимальное решение могло быть в точках 1 или 3 на рис. 3.1.

Однако при ценах с₁ = 0,84 руб и с₂ = 3,2 руб доход фирмы в точках 1 и 3 составит:

• в точке 1, когда изготовляются только пирожные

D₁ = 3,2 × 1000 = 3200 руб.

• в точке 2, когда изготовляются только булки

D₃ = 0,84 × 2000 = 1680 руб.

Из приведенных расчетов следует, что доход в точке 2

D₂ = max = 3547,16 руб > D₁ > D₃ ,

то есть доход фирмы в точке 2 наибольший.

Если бы наклон прямой D = с₁х₁ + с₂х₂ совпал бы с наклоном прямой (2), тогда оптимальных планов выпуска продукции было бы множество, а именно: во всех точках на прямой (2) в интервале между точками 1 и 2, включая эти две точки.

Попытка решить эту задачу методом производных приведут к следующему абсурдному результату:

,

т.е. булки и пирожные надо продавать бесплатно, при этом получим D = 0.

При трех неизвестных в ЗЛП, когда n = 3, строится трехмерная система координат с взаимно перпендикулярными осями х₁, х₂ и х₃. При этом система неравенств образует трехмерную объемную фигуру - многогранник, а выражение целевой функции D = с₁х₁ + с₂х₂ + с₃х₃ описывает плоскость, наклон которой зависит от значений коэффициентов с₁, с₂ и с₃. Перемещение этой плоскости вверх параллельно самой себе до верхней точки допустимой области определит координаты вершины многогранника х_1оп, х_2оп и х_3оп, где выполняется условие оптимизационной задачи D = max. В принципе можно решить графически ЗЛП при n = 3, но сложно.

При числе неизвестных больших трех, т.е. при n > 3 должна быть построена n-мерная система координат, неравенства образуют в гиперпространстве некий гипермногогранник, а целевая функция представляет собой гиперплоскость. Перемещение этой гиперплоскости в гиперпространстве параллельно самой себе приведет до верхней точки гипермногогранника, координаты вершины которого обеспечивают D = max.