2. Нули аналитической функции и их связь с полюсами

Определение 1. Точка называетсянулём аналитической функции порядка (или кратности), если

.

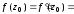
В случае точканазываетсяпростым нулём.

Имеет место следующее почти очевидное утверждение.

Теорема 2. Для того, чтобы точка была нулем - гo порядка функции, аналитической в точке , необходимо и достаточно, чтобы в некоторой окрестности этой точки имело место равенство, где аналитична в точке и . Для того, чтобы точка была полюсом порядкафункциинеобходимо и достаточно, чтобы функцияимела в этой точке нульго порядка. В этом случаепредставляется в виде где аналитическая в точке функция, причем

Пример 1. Найти нули функциии определить их порядки.

Решение.Из уравнениянаходим точки,– нули данной функции. Имеем:,, т.е. точки– нули второго порядка данной функции.

Пример 2. Найти нули функциии определить их порядки.

Решение. Полагая, получаем, чтоили.Решая эти уравнения, находим нули функции . Пусть; тогдаможно представить в виде, где функцияявляется аналитической в точке, причем. Это означает, что точка есть нуль третьего порядка. Аналогично доказывается, что и точкаявляется нулем третьего порядка. Исследуем нули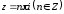. Производнаяв точках отлична от нуля. Следовательно,– простые нули функции.

Мы знаем структуру разложения функци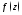и в окрестности устранимой особой точки, в окрестности полюса и в окрестности существенно особой точки (см. теорему 1). Каким будет поведение функциипри стремлениик существенно особой точкеМожет ли она стремиться к какому-нибудь пределу,Оказывается нет. Доказано следующее утверждение.

Теорема Сохоцкого. Если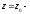существенно особая точка функциито каково бы ни было наперёд заданное число(может быть равным), существует последовательностьстремящаяся ктакая, что

3. Вычеты. Теорема Коши о вычетах

Как ни странно, но именно особые точки интересны в приложениях. С помощью них удается решить многие задачи, например задачу о вычислении сложных несобственных интегралов (см. ниже). В основе этих вычислений лежит теория вычетов, к изучению которой мы переходим.

Определение 3. Пусть изолированная особая точка функцииЧисло

гделюбой кусочно-гладкий замкнутый контур, лежащий в окрестностианалитичности функцииобходимый против часовой стрелки и охватывающий точкуназывается вычетом функциив точке

Вспоминая теорему Лорана, видим, что т.е. равен коэффициенту прив разложении функциив окрестности особой точки

Теорема Коши о вычетах. Пусть функция аналитична в односвязной областии на её кусочно-гладкой замкнутой границеза исключением конечного числа особых точек

Рис.13 лежащих внутри областиТогда

где граница обходится против часовой стрелки.

Доказательство. Окружим особые точки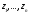 попарно не пересекающимися замкнутыми кусочно-гладкими контурами(это всегда можно сделать, так как все особые точки изолированные). Обозначим черезобласть, охватываемую контуром(см. рис. 13). Тогда областьбудетсвязной. По теореме Коши для многосвязной области имеем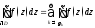(здесь все контуры обходятся против часовой стрелки). Так както имеет место равенство. Теорема доказана.

На следующей лекции будут даны формулы вычисления вычетов и их их приложения.