Лекция 12. Преобразование Лапласа и его свойства. Применение к дифференциальным уравнениям

Пусть функция является комплексной функцией действительного аргументат.е.

Определение 1. Функция называетсяоригиналом, если выполнены следующие условия:

1. 2.кусочно-непрерывна на любом конечном отрезке3. существуют постоянныеитакие, чтоПри этом число⁵называетсяпоказателем роста (или индексом) оригинала .

Например, функция Хевисайда (единичная функция):

является оригиналом с показателем роста Заметим, что если функцияудовлетворяет только условиям 2 и 3, то функцияявляется оригиналом. По этой причине множительвчасто опускают и пишут просто.

Определение 2. Пусть –оригинал. Функция называется преобразованием Лапласа функции (другие названия:изображение по Лапласу,образ преобразования Лапласа). При этом пишут

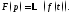
Теорема 1. Если оригинал с показателем ростато его изображениесуществует и аналитично в полуплоскостиПри этом

Доказательство. Имеем

поэтому при имеет место оценка

При отсюда получаем, что интеграл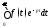абсолютно сходится при всех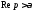и что имеет место оценка

Устремляя здесь получим, что

Итак, показано, что преобразование Лапласа существует в полуплоскости 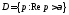и что имеет место утверждение Дифференцируя равенствопо параметру, покажем, что производная

существует при всех Это означает, чтоаналитична в областиТеорема доказана.

Замечание 1. Желая указать показатель роста оригиналабудем писать

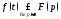или

Теорема 2 (свойства преобразования Лапласа). При указанных значениях имеют место следующие утверждения (нижеипроизвольные постоянные):

(линейность).

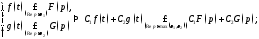
(теорема подобия).

(теорема запаздывания).

(теорема смещения).

(теорема о дифференцировании оригинала). Если оригиналы с показателем ростато

(теорема об интегрировании оригинала).

(теорема о дифференцировании изображения).

(теорема об интегрировании изображения). Пусть и интегралсходится. Тогда

Определение 3. Свёрткой функци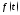й иназывается интеграл

Очевидно, что свёртка коммутативна, т.е.

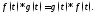
(теорема умножения). (здесь попутно утверждается, что свёртка оригиналов также является оригиналом).

(интеграл Дюамеля). Если оригиналы с показателем ростааоригинал с показателем ростато

Все эти свойства доказываются довольно просто. Докажем, например, теорему о дифференцировании оригинала. Имеем при

Мы показали справедливость свойства приАналогично показывается его справедливость при любом

Приведём теперь таблицу изображений основных функций.

Таблица 2. Преобразования Лапласа основных функций

Все формулы этой таблицы доказываются либо непосредственным вычислением изображений, либо применением свойств преобразования Лапласа. Покажем, например, справедливость формулы 6. Посколькуто формуле 2 и по свойству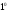будем иметьЭто высказывание имеет место, если одновременноит.е. еслиФормула 6 доказана.

Рассмотрим несколько примеров.

Пример 1. Найти изображения следующих функций: а) б)

Решение. а) Воспользуемся формулой понижения порядка и формулами 1 и 5 таблицы 2:

б) Представим функцию в видеПо таблице 2 сразу же находимОсталось найти изображение функцииВоспользуемся для этого теоремой о дифференцировании изображения:

Так как в нашем случае тоТаким образом,

Пример 2. Найти изображение функции

Решение. Можно было бы сначала вычислить интеграл, а затем найти изображение, но проще воспользоваться теоремойоб интегрировании оригинала

В нашем случае

Пример 3. Найти изображение функции

Решение. Воспользуемся теоремой об интегрировании изображения:

Сначала найдём изображение функции Тогда будем иметь

Пример 4. Найти преобразование Лапласа функции изображённой на рисунке.

Решение. Можно было бы применить теорему запаздывания, но проще вычислить изображение по определению:

Следующее утверждение показывает, как можно восстановить оригинал по изображению.

Теорема обращения Меллина. Пусть аналитическая в области функцияявляется изображением некоторого оригинала с показателем роста Тогда в каждой точкев которой функциянепрерывна, имеет место равенство

где 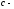произвольная постоянная, удовлетворяющая неравенству

Из теоремы Меллина вытекает следующее утверждение об умножении оригиналов.

.

где произвольная постоянная, удовлетворяющая неравенству

При использовании теоремы Меллина возникают две основные трудности. Первая из них заключается в проверке того, что функция является оригиналом, вторая –

в вычислении самого интеграла Меллина (2). Поэтому обычно применяют более простые теоремы разложения, где эти трудности преодолеваются очевидным образом.

Первая теорема обращения. Пусть функция имеет в окрестности точкилорановское разложение вида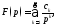сходящееся абсолютно принекоторая постоянная. Тогда оригинал длясуществует в областии имеет вид

причем этот ряд сходится абсолютно для всех

Вторая теорема обращения. Пусть функция правильная дробь (т.е.многочлены, причем степень многочленаменьше степени многочлена). Тогда для функциисуществует оригиналпричем функцияимеет вид

где вычеты вычисляются по всем нулям знаменателя

Пусть, например, надо найти оригинал функции Первый способ вычисления оригинала основан на разложениина простейшие дроби:

При этом оригинал находится по таблице 2 с использованием свойства 1⁰ линейности преобразования Лапласа. Из той же таблицы находим, что изображение 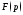существует приДругой способ основан на второй теореме разложения:

Покажем теперь, как применяется операционное исчисление к решению дифференциальных уравнений. Рассмотрим задачу Коши

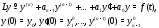
с постоянными коэффициентами Предположим, что неоднородностьи решениеявляются оригиналами, причем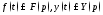Применяя теоремуо дифференцировании оригинала, будем иметь

Умножая эти равенства на соответствующие коэффициенты стоящие слева от черты, и складывая полученные результаты, будем иметь

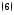
где амногочлен отй степени, коэффициенты которого зависят лишь от начальных условийПравая часть (6) называется изображением левой части уравнения (5) с учётом соответствующих начальных условий. Приравнивая его к изображению левой части (5), получим алгебраическое уравнение

называемое операторным уравнением, соответствующим задаче (5). Решением этого уравнения является функция Получено изображение решения задачи (5). Применяя теорему Меллина, получим и само решение:

Замечание. Если все начальные значения нулевые (), то и операторное уравнение (7) будет иметь более простое решение: Заметим также, что является характеристическим полиномом уравнения (5).

Пример 5. Решить задачу Коши

Решение. Пусть 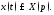Имеем

Из последнего уравнения находим, что Находим теперь оригинал-решение исходной задачи, разлагая изображение решения на простейшие дроби и используя таблицу 2:

Задачу вычисления уравнения (5) с нулевыми начальными условиями и произвольной неоднородностью можно свести к решению той же задачи, но с неоднородностьюДелается это с помощью следующего свойства преобразования Лапласа:

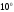(интеграл Дюамеля). Если оригиналы с показателем ростааоригинал с показателем ростато

Рассмотрим задачу

Чтобы решить её, рассмотрим вспомогательную задачу

Покажем, что если известно решение 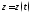этой задачи, торешение задачи (8) является свёрткой её неоднородности с производной от решения вспомогательной задачи (9):

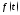Действительно, формула с учетом того, чтоперепишется в видегдеизображения функцийисоответственно. Операторным решением задачи (8) является функция(см. замечание), а операторным решением вспомогательной задачи (9) является функцияпоэтомуОтсюда и из формулыполучаем, чтот.е. имеет место формула (10).

Пример 6.Решить задачу Коши

Решение.Решим сначала вспомогательную задачу Оператор-

ным решением для неё будет функция Так как

Решение же исходной задачи находим по формуле (10):