
- •Глава 10. Элементы векторного анализа
- •10.1. Скалярные и векторные поля
- •10.2. Работа векторного поля. Циркуляция
- •10.3. Потенциальное векторное поле
- •10.4. Ротор векторного поля
- •10.4. Поток и дивергенция векторного поля
- •10.5. Соленоидальные векторные поля
- •10.6. Контрольные вопросы
- •10.7. Задания для самостоятельной работы
10.2. Работа векторного поля. Циркуляция
Дадим физическую
интерпретацию криволинейного интеграла
второго рода. Если в некоторой области
![]() задано непрерывное силовое поле
задано непрерывное силовое поле![]() ,
то при перемещении материальной точки
вдоль гладкой ориентированной кривойL
поле совершает некоторую работу А.
Для её определения разобьём линию L
на
,
то при перемещении материальной точки
вдоль гладкой ориентированной кривойL
поле совершает некоторую работу А.
Для её определения разобьём линию L
на
![]() дуг точками
дуг точками![]() ,
,![]() ,
…,
,
…,![]() (рис. 16). Пусть
(рис. 16). Пусть![]() произвольная точка дуги
произвольная точка дуги![]() .
Обозначим
.
Обозначим![]() – единичный вектор касательнойL
в этой точке и
– единичный вектор касательнойL
в этой точке и
![]() – длину дуги
– длину дуги![]() .
.
Р
Рис.5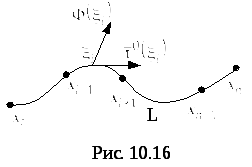
![]() можно приближённо вычислить с помощью
скалярного произведения
можно приближённо вычислить с помощью
скалярного произведения![]() .
Тогда приближённо работа есть
.
Тогда приближённо работа есть![]() .
.
За работу А на всей кривой L естественно принять предел
![]() .
.
Если этот предел
существует, то он является криволинейным
интегралом I
рода от скалярной функции
![]() ,
т.е. это криволинейный интегралII
рода. Таким образом, работа А
по перемещению материальной точки в
непрерывном силовом поле выражается
криволинейным интегралом II
рода:
,
т.е. это криволинейный интегралII
рода. Таким образом, работа А
по перемещению материальной точки в
непрерывном силовом поле выражается
криволинейным интегралом II
рода:
![]() .
(2)
.
(2)
Покажем, что работа
поля
![]() вдоль любой векторной линии этого поля
отлична от нуля. ПустьL
– векторная линия, тогда
вдоль любой векторной линии этого поля
отлична от нуля. ПустьL
– векторная линия, тогда
![]() вектор
вектор![]() параллелен
параллелен![]() .
Тогда скалярное произведение
.
Тогда скалярное произведение![]() ,
тогда
,
тогда![]() ,
причём кривая может быть замкнутой.
,
причём кривая может быть замкнутой.
Определение 1.
Работа векторного поля
![]() вдоль замкнутой кривойL
называется
циркуляцией
этого поля:
вдоль замкнутой кривойL
называется
циркуляцией
этого поля:
![]() .
.
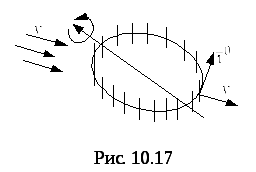
Ф
Рис.6![]() – поле скоростей
– поле скоростей![]() текущей жидкости. Поместим в это поле
колёсико с лопастями, расположенными
по окружностиL
этого колеса (рис.6). Частицы жидкости,
действуя на эти лопасти, будут создавать
вращательные моменты, суммарное действие
которых приводит колесо в движение –
вращение вокруг своей оси. Вращательное
действие поля
текущей жидкости. Поместим в это поле
колёсико с лопастями, расположенными
по окружностиL
этого колеса (рис.6). Частицы жидкости,
действуя на эти лопасти, будут создавать
вращательные моменты, суммарное действие
которых приводит колесо в движение –
вращение вокруг своей оси. Вращательное
действие поля
![]() в каждой точке будет характеризоваться
проекцией
в каждой точке будет характеризоваться
проекцией![]() на касательную
на касательную![]() ,
т.е. скалярным произведением
,
т.е. скалярным произведением![]() .
Суммирование вращательных действий
жидкости по всему контуру колёсика
приводит к понятию циркуляции вектора
.
Суммирование вращательных действий
жидкости по всему контуру колёсика
приводит к понятию циркуляции вектора![]() .
.
Ф
![]() определяет его вращательную способность
в данном направлении и характеризует
завихрённость поля в этом направлении.
Чем меньше угол между касательной и
вектором поля, тем большеС,
а следовательно и завихрённость.
определяет его вращательную способность
в данном направлении и характеризует
завихрённость поля в этом направлении.
Чем меньше угол между касательной и
вектором поля, тем большеС,
а следовательно и завихрённость.
Пример 2.
Вычислить циркуляцию векторного поля
![]() вдоль замкнутого контура
вдоль замкнутого контура![]() ,
являющегося границей части сферы
,
являющегося границей части сферы![]() ,
расположенной в первом октанте:
,
расположенной в первом октанте:![]() ,
,![]() ,
,![]() ,
причем направление обхода контура
таково, что в плоскостиОху
движение происходит от точки
,
причем направление обхода контура
таково, что в плоскостиОху
движение происходит от точки
![]() к
к![]() .
.
Решение.
Контур
![]() состоит из трех кривых
состоит из трех кривых![]() ,
каждая из которых является дугой
единичной окружности, лежащей
соответственно в координатной плоскостиОху,
Оуz,
Oxz.
Поэтому
,
каждая из которых является дугой
единичной окружности, лежащей
соответственно в координатной плоскостиОху,
Оуz,
Oxz.
Поэтому
![]() ,
,
![]() .
.
Найдем интеграл
![]() по кривой
по кривой![]() .
Так как кривая
.
Так как кривая![]() лежит в плоскостиОху,
то
лежит в плоскостиОху,
то
![]() ,
,![]() и
и![]() ,
где
,
где![]() ,
,![]() ,
,![]() .
Запишем параметрическое уравнение
.
Запишем параметрическое уравнение![]() :
:![]() ,
,![]() ,
,![]() .
Получаем
.
Получаем
![]()
![]() .
.
Точно так же
вычисляются интегралы
![]() и
и![]() .
При этом
.
При этом![]() .
Следовательно,
.
Следовательно,![]() .
.
10.3. Потенциальное векторное поле
Определение 2.
Векторное поле
![]() называетсяпотенциальным
в области
называетсяпотенциальным
в области
![]() ,
если существует такое скалярное поле
,
если существует такое скалярное поле![]() ,
что для всех точек этой области
вектор-функция
,
что для всех точек этой области
вектор-функция![]() является градиентом этого скалярного
поля
является градиентом этого скалярного
поля![]() :
:
![]() .
.
Скалярное поле
![]() называетсяпотенциалом
векторного поля
называетсяпотенциалом
векторного поля
![]() .
Потенциальное поле является одним из
наиболее простых полей, так как
определяется одной скалярной функцией
.
Потенциальное поле является одним из
наиболее простых полей, так как
определяется одной скалярной функцией![]() ,
в то время как произвольное векторное
поле – тремя скалярными функциями
,
в то время как произвольное векторное
поле – тремя скалярными функциями![]() .
.
Теорема 1. Если
поле
![]() потенциально, то его потенциал определяется
однозначно с точностью до произвольного
постоянного слагаемого.
потенциально, то его потенциал определяется
однозначно с точностью до произвольного
постоянного слагаемого.
Пусть поле
![]() имеет два потенциала
имеет два потенциала![]() и
и![]() ,
т.е.
,
т.е.![]() и
и![]() .
Тогда
.
Тогда![]() и, следовательно,
и, следовательно,![]() .
Таким образом, получаем, что
.
Таким образом, получаем, что![]() .<
.<
Теорема 2. Если
поле
![]() потенциально в областиV,
то работа этого поля (криволинейный
интеграл второго рода) не зависит от
формы пути, соединяющий две любые точки
из V.
Потенциал
потенциально в областиV,
то работа этого поля (криволинейный
интеграл второго рода) не зависит от
формы пути, соединяющий две любые точки
из V.
Потенциал
![]() с точностью до произвольной постоянной
определяется криволинейным интегралом
второго рода
с точностью до произвольной постоянной
определяется криволинейным интегралом
второго рода ,
взятому по произвольной кривой
,
взятому по произвольной кривой![]() ,
соединяющей точки
,
соединяющей точки![]() и
и![]() ,
где
,
где![]() – фиксированная точка, а
– фиксированная точка, а![]() – текущая точка.
– текущая точка.
Работа А
поля
![]() по некоторому путиL,
соединяющему точки
по некоторому путиL,
соединяющему точки
![]() и
и![]() ,
вычисляется по формуле (11):
,
вычисляется по формуле (11):
![]() .
.
Поле
![]() потенциально, тогда существует потенциал
потенциально, тогда существует потенциал![]() ,
причем
,
причем![]() .
Тогда скалярное произведение
.
Тогда скалярное произведение
![]() ,
,
Для простоты
преобразований пусть
![]() плоская кривая, заданная параметрическими
уравнениями
плоская кривая, заданная параметрическими
уравнениями![]() ,
,![]() ,
,![]() ,
причем начало в точке
,
причем начало в точке![]() ,
которой соответствует значение параметра
,
которой соответствует значение параметра![]() ,
а конечной точки
,
а конечной точки![]() соответствует значение параметра
соответствует значение параметра![]() ,
т.е.
,
т.е.![]() ,
,![]() .
Тогда
.
Тогда
![]()
=![]()
![]()
![]() .
.
Т.е потенциал
![]() определяется по формуле
определяется по формуле
![]() (3)
(3)
Откуда следует,
что работа не зависит от формы пути, а
зависит от положения начальной
![]() и конечной
и конечной![]() точек.<
точек.<
Задача отыскания
потенциала
![]() поля
поля![]() тесно связано с задачей восстановления
функции трёх переменных по её полному
дифференциалу.
тесно связано с задачей восстановления
функции трёх переменных по её полному
дифференциалу.
Теорема 3.
Пусть векторное поле задано функцией
![]() ,
которая непрерывно дифференцируема в
области
,
которая непрерывно дифференцируема в
области![]() .
Для того, чтобы выражение
.
Для того, чтобы выражение
![]() (4)
(4)
было полным
дифференциалом некоторой функции
![]() ,
необходимо и достаточно, чтобы поле
,
необходимо и достаточно, чтобы поле![]() было потенциальным.
было потенциальным.
Необходимость.
Пусть (4) есть полный дифференциал
![]() ,
то с одной стороны по определению
,
то с одной стороны по определению![]() ,
а с другой стороны
,
а с другой стороны![]() ,
откуда
,
откуда![]() .
Т.е.
.
Т.е.![]() ,
а, следовательно,
,
а, следовательно,![]() – потенциальное поле.
– потенциальное поле.
Достаточность.
Пусть
![]() – потенциально, тогда существует функция
– потенциально, тогда существует функция![]() ,
такая, что
,
такая, что![]() .
По определению градиента
.
По определению градиента![]() ,
,![]() ,
,![]() ,
тогда получаем
,
тогда получаем![]() .<
.<
Для того,
чтобы найти функцию
![]() по её полному дифференциалу необходимо
применить формулу (3), т.е. с точностью
до произвольного постоянного слагаемого
вычислить криволинейный интеграл по
любой кривой, соединяющей две точки
по её полному дифференциалу необходимо
применить формулу (3), т.е. с точностью
до произвольного постоянного слагаемого
вычислить криволинейный интеграл по
любой кривой, соединяющей две точки![]() и
и![]() т.е.
т.е.
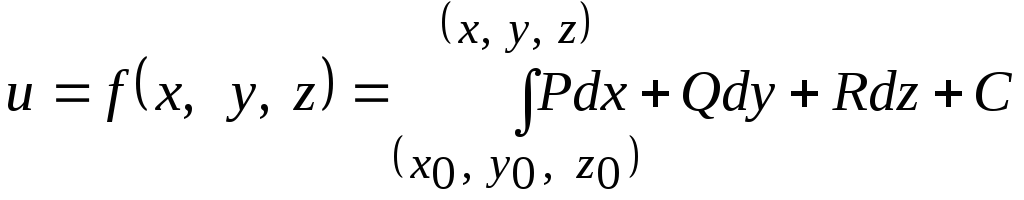 .
.
Теперь естественно возникает вопрос: когда, при каких условиях векторное поле является потенциальным?
Теорема 4.
Для того чтобы работа векторного поля
![]() не
зависела от формы пути, соединяющего
две точки в области, необходимо и
достаточно, чтобы циркуляция по любому
замкнутому контуру, лежащему в этой
области, была равна нулю.
не
зависела от формы пути, соединяющего
две точки в области, необходимо и
достаточно, чтобы циркуляция по любому
замкнутому контуру, лежащему в этой
области, была равна нулю.
Необходимость.
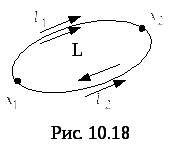
Пусть работа не зависит от пути. Возьмём
контур ![]() (рис. 10.18).
(рис. 10.18).
Рис.7![]()
Рис.18![]()
Достаточность.
Пусть ![]() ,
тогда
,
тогда ![]() .
Получаем
.
Получаем
![]() ,
,
т.е. работа не зависит от пути.
