
- •Глава 10. Элементы векторного анализа
- •10.1. Скалярные и векторные поля
- •10.2. Работа векторного поля. Циркуляция
- •10.3. Потенциальное векторное поле
- •10.4. Ротор векторного поля
- •10.4. Поток и дивергенция векторного поля
- •10.5. Соленоидальные векторные поля
- •10.6. Контрольные вопросы
- •10.7. Задания для самостоятельной работы
10.4. Ротор векторного поля
Понятие ротора и его вычисление. С понятием циркуляции тесно связано понятие ротора или вихря. Циркуляция характеризует вращательную способность или завихрённость поля вдоль некоторого контура, а локальной характеристикой поля является ротор.
Р
Рис.38
Рис.8![]() и какой-либо контур
и какой-либо контур![]() ,
окружающий выбранную точку
,
окружающий выбранную точку![]() (рис. 8). Площадь, ограниченная контуром
(рис. 8). Площадь, ограниченная контуром![]() ,
равнаs.
Тогда отношение
,
равнаs.
Тогда отношение
![]() есть средняя плотность циркуляции
вектора
есть средняя плотность циркуляции
вектора![]() на площадкеs.
Плотность циркуляции в точке
на площадкеs.
Плотность циркуляции в точке
![]() характеризуется пределом, когда
характеризуется пределом, когда![]() ,
т.е.
,
т.е.
![]() (5)
(5)
Если этот предел
существует, то он даёт величину
завихрённости поля в точке
![]() .
.
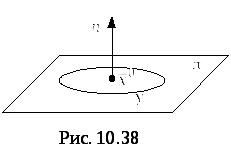
![]() – пространственное, то можно говорить
о завихрённости в каком-либо направлении
– пространственное, то можно говорить
о завихрённости в каком-либо направлении![]() .
Проведём через точку
.
Проведём через точку![]() плоскость
плоскость![]() ,
перпендикулярную выбранному направлению
,
перпендикулярную выбранному направлению![]() ,
и рассмотрим в ней какой-либо контур
,
и рассмотрим в ней какой-либо контур![]() ,
охватывающий точку
,
охватывающий точку![]() (рис.8). Тогда предел (5) даёт завихрённость
поля в направлении
(рис.8). Тогда предел (5) даёт завихрённость
поля в направлении![]() .
.
Определение 3.
Ротором
векторного поля
![]() в точке
в точке![]() называется вектор, проекция которого
на направление
называется вектор, проекция которого
на направление![]() равна пределу отношения циркуляции
векторного поля по плоскому контуру
равна пределу отношения циркуляции
векторного поля по плоскому контуру![]() ,
перпендикулярному этому направлению,
к величине площади
,
перпендикулярному этому направлению,
к величине площади![]() ,
охваченной контуром
,
охваченной контуром![]() ,
когда
,
когда![]() стягивается в точку
стягивается в точку![]() .
.
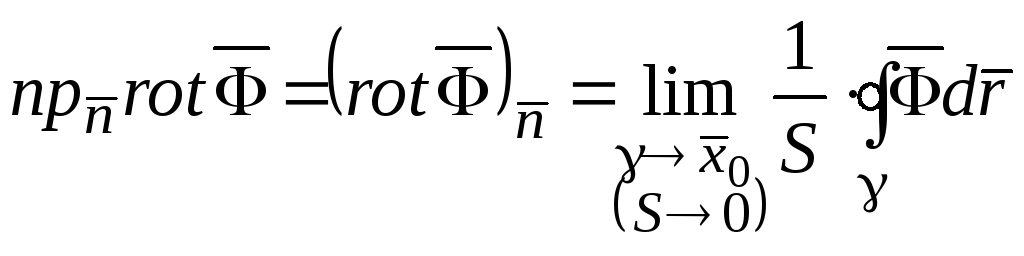 . (6)
. (6)
Заметим, что данное определение не зависит от выбора системы координат, т.е. оно инвариантно.
Получим формулу
вычисления
![]() в декартовой
системе координат.
в декартовой
системе координат.
Теорема5.
Пусть в каждой точке
![]() задано непрерывно дифференцируемое
поле
задано непрерывно дифференцируемое
поле![]() .
Тогда в точке
.
Тогда в точке![]() существует
существует
![]() ,вычисляемый по
формуле:
,вычисляемый по
формуле:
![]() . (7)
. (7)
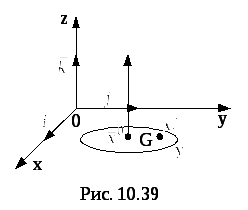
![]() на осьOz.
Пусть
на осьOz.
Пусть
![]() – контур, лежащий в плоскостиОху,
ограничивающей область G.
Воспользуемся формулой Грина (рис. 9)
– контур, лежащий в плоскостиОху,
ограничивающей область G.
Воспользуемся формулой Грина (рис. 9)
![]() .
.
Применим к двойному интегралу теорему о среднем:
Рис.9![]()
и подставим последнее в (6):
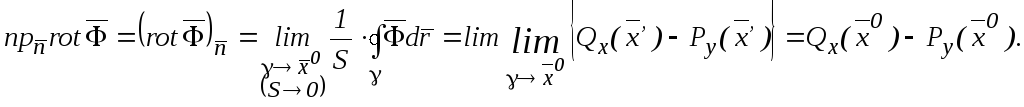 Аналогично
вычисляем проекции
Аналогично
вычисляем проекции
![]() на орты
на орты
![]() и
и![]() .<
.<
Вектор
![]() символически записывается следующим
образом:
символически записывается следующим
образом:
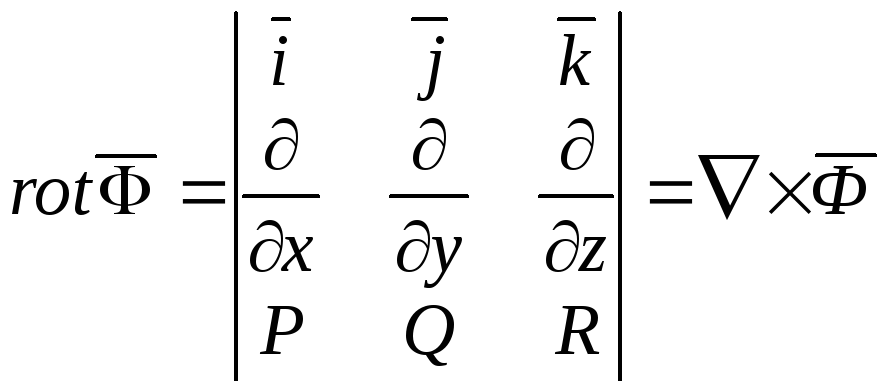 ,
,
где
![]() – оператор Гамильтона.
– оператор Гамильтона.
Легко доказать
следующие свойства
![]() :
:
![]() .
.
![]() .
.
![]() .
.
Пример 3.
Найти ротор поля скорости
![]() твердого тела, вращающегося вокруг
неподвижной точки с мгновенной угловой
скоростью
твердого тела, вращающегося вокруг
неподвижной точки с мгновенной угловой
скоростью
![]() .
.
Решение.
Найдём сначала линейную скорость
![]() .
Из курса физики известно, что
.
Из курса физики известно, что
![]() .
.
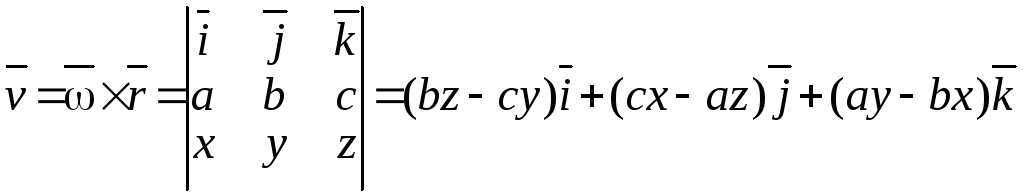 .
.
Тогда
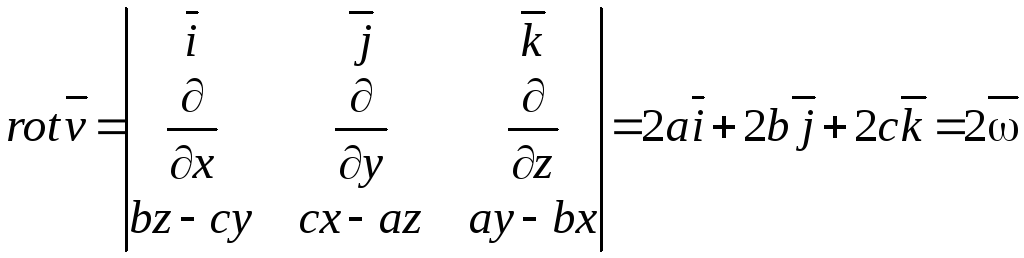 ;
;
![]() .
.
Таким образом,
![]() ,
характеризуя «вращательную компоненту»
поля скоростей, равен удвоенной скорости
вращения.
,
характеризуя «вращательную компоненту»
поля скоростей, равен удвоенной скорости
вращения.
Пример 4.
Найти
![]() .
.
Решение.
![]() .
.
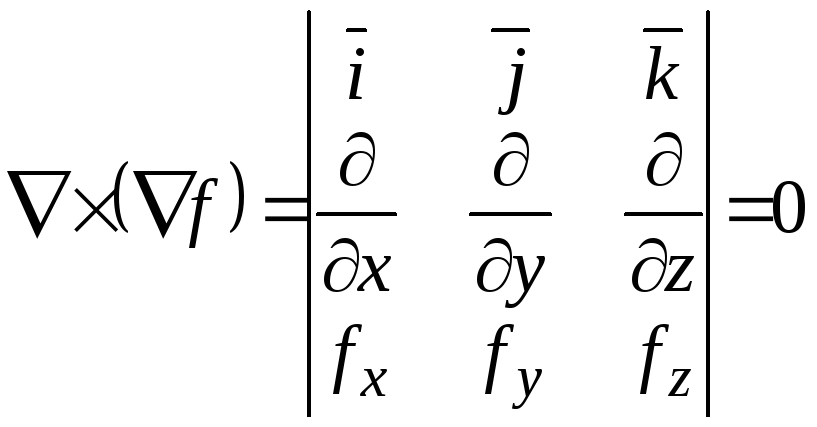 .
.
Следовательно,
вектор
![]() параллелен вектору
параллелен вектору![]() .
.
С помощью
![]() можно
обобщить формулу Грина на пространственный
случай. Таким обобщением является
формула Стокса, которая связывает
циркуляцию векторного поля с потоком
ротора через поверхность, натянутую на
этот контур. При этом говорят, что
поверхность можно натянуть на контур
можно
обобщить формулу Грина на пространственный
случай. Таким обобщением является
формула Стокса, которая связывает
циркуляцию векторного поля с потоком
ротора через поверхность, натянутую на
этот контур. При этом говорят, что
поверхность можно натянуть на контур![]() ,
если существует кусочно-гладкая
ориентированная поверхность
,
если существует кусочно-гладкая
ориентированная поверхность![]() ,
лежащая в областиV
и имеющая
,
лежащая в областиV
и имеющая
![]() своей границей.
своей границей.
Трехмерную область
V
будем называть поверхностно-односвязанной,
если на любой контур
![]() можно натянуть поверхность
можно натянуть поверхность![]() ,
целиком лежащую в
V.
Примеры поверхностно неодносвязной
области – шар, через который проходит
цилиндрический туннель.
,
целиком лежащую в
V.
Примеры поверхностно неодносвязной
области – шар, через который проходит
цилиндрический туннель.
П
Рис.40
Рис.10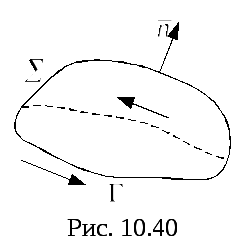
![]() – ориентированная поверхность, натянутая
на контур
– ориентированная поверхность, натянутая
на контур![]() рис.10. Нормаль к поверхности
рис.10. Нормаль к поверхности![]() выберем таким образом, чтобы направление
вектора
выберем таким образом, чтобы направление
вектора![]() соответствовало положительному обходу
контура
соответствовало положительному обходу
контура![]() .
Направление обхода контура
.
Направление обхода контура![]() будем считать положительным, если при
обходе по контуру
будем считать положительным, если при
обходе по контуру![]() область
область![]() остается все время слева. Если смотреть
с конца вектора
остается все время слева. Если смотреть
с конца вектора![]() ,
то обход контура осуществляется против
часовой стрелки. В этом случае говорят,
что направление обхода
,
то обход контура осуществляется против
часовой стрелки. В этом случае говорят,
что направление обхода![]() и ориентация
и ориентация![]() согласованы.
согласованы.
Теорема 6.(Стокс)
Пусть V
-
поверхностно-односвязаная область,
![]() -
кусочно-гладкий контур в V
и
-
кусочно-гладкий контур в V
и
![]() -
кусочно-гладкая поверхность, натянутая
на
-
кусочно-гладкая поверхность, натянутая
на
![]() и лежащая в
V.
Пусть в области V
задано векторное поле
и лежащая в
V.
Пусть в области V
задано векторное поле
![]() ,
непрерывное и дифференцируемое в во
всех точках области и
,
непрерывное и дифференцируемое в во
всех точках области и![]() также непрерывен в
V.
Тогда циркуляция поля
также непрерывен в
V.
Тогда циркуляция поля
![]() по контуру
по контуру
![]() равна потоку ротора
равна потоку ротора
![]() через
через
![]() ,
т.е. справедлива формула Стокса
,
т.е. справедлива формула Стокса
![]() , (8)
, (8)
причём направление
обхода
![]() и ориентация
и ориентация![]() согласованы.
согласованы.
Разобьём поверхность
![]() наn
частей
наn
частей
![]() ,
ограниченных контурами
,
ограниченных контурами![]() ,
,![]() .
Рассмотримi-й
элемент
.
Рассмотримi-й
элемент
![]() поверхности
поверхности![]() .
Возьмём произвольную точку
.
Возьмём произвольную точку
![]() и проведём через неё нормаль
и проведём через неё нормаль
![]() и касательную плоскость
и касательную плоскость
![]() к
к
![]() .
Обозначим через
.
Обозначим через
![]() проекцию контура
проекцию контура![]() ,
,![]() – площадь поверхности
– площадь поверхности![]() ,
а через
,
а через![]() – площадь проекции
– площадь проекции![]() на
на
![]() .
Из определения ротора следует равенство
.
Из определения ротора следует равенство
![]() .
.
При достаточно
мелком разбиении это равенство будет
справедливо для контура
![]() поверхности
поверхности![]() ,
т.е.
,
т.е.
![]() .
.
Суммируя последнее
равенство по всем
![]() ,
получим
,
получим
![]() . (9)
. (9)
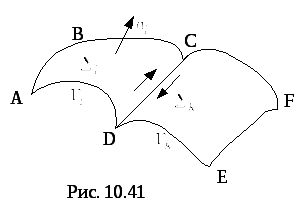
П
Рис.11![]() и
и
![]() ,
в соответствии с правилом согласования
направления обхода контура и нормали,
их общая часть границы обходиться в
противоположных направлениях (рис. 11).
,
в соответствии с правилом согласования
направления обхода контура и нормали,
их общая часть границы обходиться в
противоположных направлениях (рис. 11).
![]() .
.
Суммируя контурные
интегралы по всем i,
получаем интеграл по общему контуру,
т.е.
![]() .
Тогда (9) принимает вид
.
Тогда (9) принимает вид
![]() .
.
Сумма в правой
части является интегральной для
поверхностного интеграла
![]() .
Переходя здесь к пределу при
.
Переходя здесь к пределу при![]()
![]() ,
получим формулу Стокса (8).<
,
получим формулу Стокса (8).<
Замечание.
Из формулы Стокса следует, что если
![]() и
и![]() – две поверхности, натянутые на контур
– две поверхности, натянутые на контур![]() ,
то потоки поля
,
то потоки поля![]() через них равны.
через них равны.
Теорема 7.
(необходимое и достаточное условие
потенциальности векторного поля) Для
того, чтобы непрерывно дифференцируемое
векторное поле
![]() было потенциальным в поверхностно-односвязанной
области V
необходимо и достаточно, чтобы оно было
безвихревым, т.е.
было потенциальным в поверхностно-односвязанной
области V
необходимо и достаточно, чтобы оно было
безвихревым, т.е.
![]()
![]() .
.
Необходимость.
Пусть поле
![]() потенциально, тогда существует его
потенциал
потенциально, тогда существует его
потенциал![]() ,
т.е.
,
т.е.![]() .
Получаем
.
Получаем
![]() .
.
Достаточность.
Пусть поле
![]() безвихревое поле, т.е.
безвихревое поле, т.е.![]() для любой точки
для любой точки![]() .
Так как областьV
поверхностно-односвязная, то по теореме
Стокса для произвольного контура
.
Так как областьV
поверхностно-односвязная, то по теореме
Стокса для произвольного контура
![]() существует интеграл
существует интеграл![]() ,
который не зависит от пути интегрирования,
т.е. кривой, соединяющей точки
,
который не зависит от пути интегрирования,
т.е. кривой, соединяющей точки![]() и
и![]() .
Если точка
.
Если точка![]() зафиксирована, то интеграл является
функцией
зафиксирована, то интеграл является
функцией![]() .
Обозначим её
.
Обозначим её
![]() .
.
Покажем, что
![]() .
Так как интеграл не зависит от формы
пути интегрирования, то
.
Так как интеграл не зависит от формы
пути интегрирования, то
![]()
![]() ,
т.к.
,
т.к.
![]() .
.
![]() В
качестве пути интегрирования взят
отрезок, параллельный оси Ох,
согласно определению производной,
теоремы о среднем, а также в силу
непрерывности
В
качестве пути интегрирования взят
отрезок, параллельный оси Ох,
согласно определению производной,
теоремы о среднем, а также в силу
непрерывности
![]() ,
получаем
,
получаем
![]()
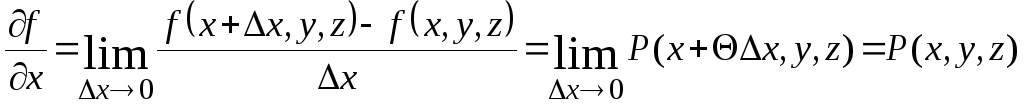 .
.
Аналогично
показывается, что
![]() и
и![]() ,
следовательно
,
следовательно![]() .<
.<
Пример 5.
Показать, что поле
![]() потенциально и найти его потенциал.
потенциально и найти его потенциал.
Решение.
![]()
![]() .
.
Так как
![]() ,
то поле
,
то поле![]() потенциально. Найдем потенциал
потенциально. Найдем потенциал![]() поля
поля![]() .
.
Фиксируем точку
![]() ,
рассмотрим произвольную точку
,
рассмотрим произвольную точку![]() .
Тогда
.
Тогда![]() .
.
Л
Рис.12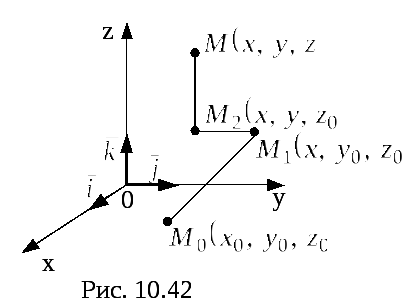
![]() (рис.12), где отрезок
(рис.12), где отрезок![]() параллелен осиОх,
отрезок
параллелен осиОх,
отрезок
![]() – осиОу, а
отрезок
– осиОу, а
отрезок
![]() – осиОz.
Вдоль
– осиОz.
Вдоль
![]() имеем
имеем![]() ,
,![]() ,
а следовательно,
,
а следовательно,![]() .
Вдоль
.
Вдоль![]() постоянно
постоянно![]() и
и![]() ,
откуда
,
откуда![]() ,
а вдоль
,
а вдоль![]() обе переменные
обе переменные![]() и
и![]() – постоянны, а это значит, что
– постоянны, а это значит, что![]() .
Тогда
.
Тогда
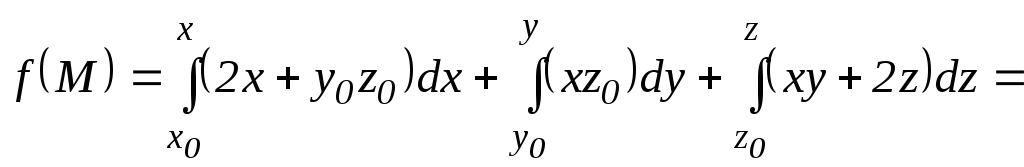
![]()
![]()
![]() .
.
