
- •Глава 10. Элементы векторного анализа
- •10.1. Скалярные и векторные поля
- •10.2. Работа векторного поля. Циркуляция
- •10.3. Потенциальное векторное поле
- •10.4. Ротор векторного поля
- •10.4. Поток и дивергенция векторного поля
- •10.5. Соленоидальные векторные поля
- •10.6. Контрольные вопросы
- •10.7. Задания для самостоятельной работы
10.4. Поток и дивергенция векторного поля
Пусть
![]() – гладкая ориентированная поверхность,
ориентация которой определяется её
нормалью
– гладкая ориентированная поверхность,
ориентация которой определяется её
нормалью![]() .
.
Определение
4. Потоком
векторного поля
![]() через поверхность
через поверхность![]() называется поверхностный интеграл
второго рода
называется поверхностный интеграл
второго рода
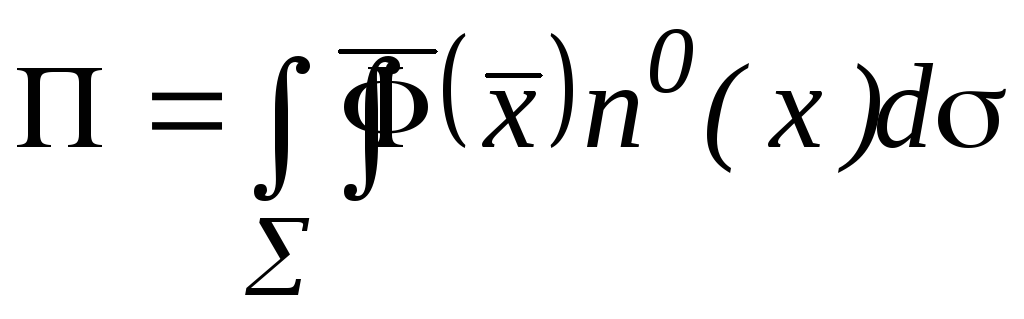
Укажем ещё
один способ вычисления поверхностного
интеграла второго рода через поверхность,
заданную в неявном виде уравнения
![]() .
Её можно рассматривать как поверхность
уровня
.
Её можно рассматривать как поверхность
уровня![]() в скалярном поле
в скалярном поле![]() ,
нормалькоторого
направлена по градиенту в сторону
возрастания С.
Так как
,
нормалькоторого
направлена по градиенту в сторону
возрастания С.
Так как
![]() ,
тогда
,
тогда
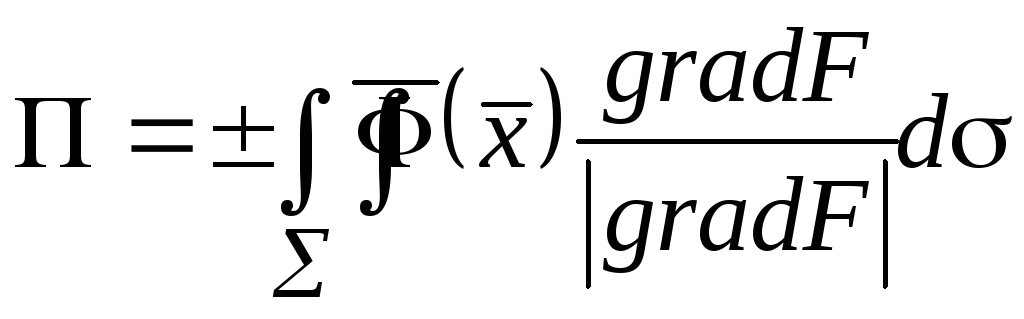 . (10)
. (10)
Выражение (10) представляет собой поверхностный интеграл первого рода. Знак выбирается в зависимости ориентации поверхности.
П
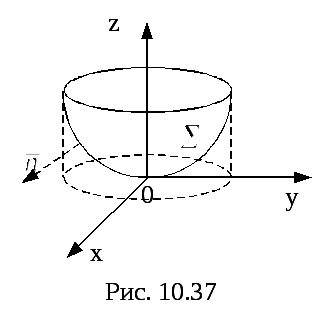
![]() через внешнюю поверхность параболоида
через внешнюю поверхность параболоида![]() ,
отсечённого плоскостью
,
отсечённого плоскостью![]() (рис.13).
(рис.13).
Р
Рис.37![]() ,
,![]() .
Направление градиентаF
совпадает с направлением нормали
.
Направление градиентаF
совпадает с направлением нормали
![]() :
:
![]() .
.
![]() .
.
По формуле (10) получим
 .
<
.
<
Рассмотрим поток
скорости жидкости
![]() через поверхность Σ:
через поверхность Σ:
![]() .
.
Если векторы
![]() и
и![]() образуют острый угол, то величина
образуют острый угол, то величина![]() ,
если – тупой, то
,
если – тупой, то![]() .
Поэтому поток
.
Поэтому поток![]() есть, вообще говоря, не абсолютное
количество жидкости, прошедшее через
поверхность
есть, вообще говоря, не абсолютное
количество жидкости, прошедшее через
поверхность![]() независимо от направления, аизбыток
жидкости,
протекающей в сторону положительной
нормали
независимо от направления, аизбыток
жидкости,
протекающей в сторону положительной
нормали
![]() .
.
Величину потока
![]() поля через замкнутую поверхность
поля через замкнутую поверхность![]() можно рассматривать как разность между
количеством жидкости, поступающей в
область, ограниченную
можно рассматривать как разность между
количеством жидкости, поступающей в
область, ограниченную![]() ,
и вытекающей из неё. Если поток положителен,
то жидкости вытекает больше, чем втекает,
и наоборот, если отрицателен, то жидкости
втекает больше, чем вытекает. Если
,
и вытекающей из неё. Если поток положителен,
то жидкости вытекает больше, чем втекает,
и наоборот, если отрицателен, то жидкости
втекает больше, чем вытекает. Если![]() ,
может означать, что в области, ограниченной
,
может означать, что в области, ограниченной![]() ,
нет источников и стоков, или их количество
таково, что их общая мощность равна
нулю.
,
нет источников и стоков, или их количество
таково, что их общая мощность равна
нулю.
Величина потока
вектора
![]() через замкнутую поверхность
через замкнутую поверхность![]() является интегральной (суммарной)
характеристикой поля вV
и лишь приближённо позволяет судить о
наличии источников и стоков. Удобнее
ввести локальную характеристику поля.
Такой характеристикой является
дивергенция
(плотность
потока в точке).
является интегральной (суммарной)
характеристикой поля вV
и лишь приближённо позволяет судить о
наличии источников и стоков. Удобнее
ввести локальную характеристику поля.
Такой характеристикой является
дивергенция
(плотность
потока в точке).
Дадим определение
дивергенции для произвольного векторного
поля
![]() в областиV.
Пусть
в областиV.
Пусть
![]()
![]() .
Окружим
.
Окружим![]() замкнутой поверхностью
замкнутой поверхностью![]() ,
которая ограничивает область
,
которая ограничивает область![]() .
Среднее значение потока по
.
Среднее значение потока по![]() есть поток через
есть поток через![]() ,
делённый на объём
,
делённый на объём![]() :
:
![]()
Определение 5.
Дивергенцией
векторного поля
![]() в точке
в точке![]() называется предел средней плотности
потока
называется предел средней плотности
потока![]() через замкнутую поверхность
через замкнутую поверхность![]() ,
окружающую точку
,
окружающую точку![]() ,
когда поверхность
,
когда поверхность![]() стягивается в точку
стягивается в точку![]() ,
если он существует и не зависит от вида
поверхности
,
если он существует и не зависит от вида
поверхности![]() .
.
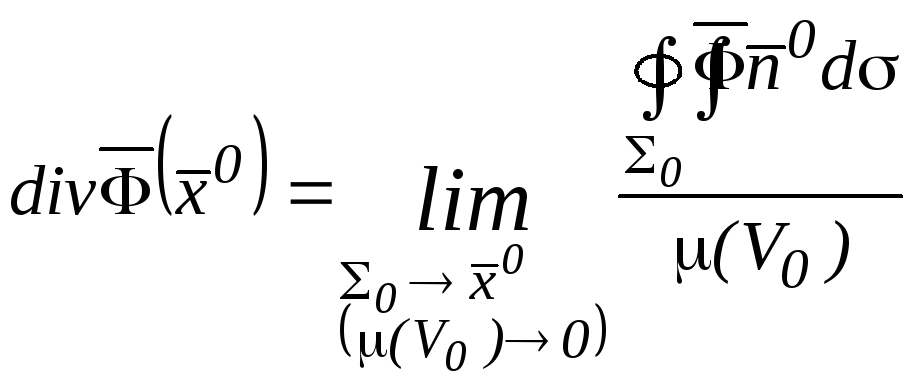 , (11)
, (11)
или
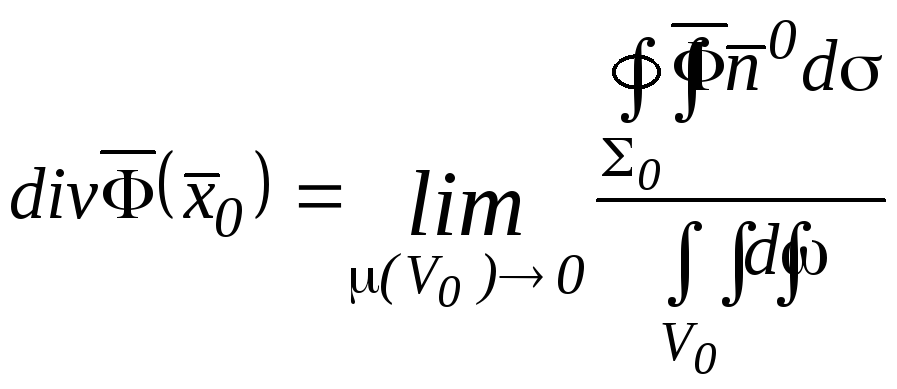 .
.
Заметим, что это определение дивергенции не зависит от системы координат.
Теорема 8.
Если в области
![]() определено векторное поле
определено векторное поле![]() ,
непрерывное вместе с частными производными
,
непрерывное вместе с частными производными![]() ,
,![]() ,
,![]() ,
то в любой точке
,
то в любой точке![]() ,
существует
,
существует![]() и имеет место формула
и имеет место формула
![]() . (12)
. (12)
Запишем формулу Остроградского-Гаусса
для области
![]() ,
содержащей точку
,
содержащей точку![]() ,
ограниченную поверхностью
,
ограниченную поверхностью![]() ,
,![]() .
По теореме о среднем для тройного
интеграла имеем, что существует точка
.
По теореме о среднем для тройного
интеграла имеем, что существует точка![]() ,
такая, что
,
такая, что
![]() .
.
Подставим это выражение в (12) и, учитывая непрерывность частных производных, получим
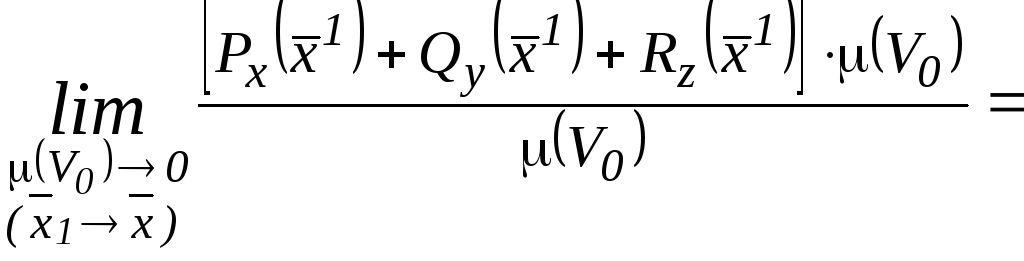
![]() .
<
.
<
Из формулы (12) следует, что формулу Остроградского-Гаусса можно записать в векторном виде. Т.к.
![]() ,
,
то
![]() , (13)
, (13)
т. е. поток вектора
![]() через внешнюю сторону замкнутой
поверхности
через внешнюю сторону замкнутой
поверхности![]() равен тройному интегралу от
равен тройному интегралу от![]() по области
по области![]() ,
ограниченной поверхностью
,
ограниченной поверхностью![]() .
Формула Остроградского-Гаусса в векторном
виде (13) не зависит от выбора системы
координат, т.е. инвариантна относительно
системы координат.
.
Формула Остроградского-Гаусса в векторном
виде (13) не зависит от выбора системы
координат, т.е. инвариантна относительно
системы координат.
Дивергенцию векторного поля можно записать с помощью оператора Гамильтона:
![]() .
.
Пример 6. Найти
дивергенцию поля
![]() в точке
в точке![]() .
.
Решение. Согласно определению дивергенции векторного поля находим
![]() .
.
Пример 7.
Вычислить поток вектора
![]() через замкнутую поверхность
через замкнутую поверхность![]() .
.
Решение. По определению потока и по формуле (40) будем иметь:
![]() ,
,
т.е. поток радиуса
вектора
![]() через замкнутую поверхность
через замкнутую поверхность![]() равен утроенному объёму тела, замкнутого
внутри этой поверхности.
равен утроенному объёму тела, замкнутого
внутри этой поверхности.
