Лекция 2. Десятичная система счисления План

1. Запись чисел в десятичной системе счисления.

2. Сравнение чисел.

3. Сложение.

4. Вычитание.

5. Умножение.

6. Деление.

Содержание

1. Из всех позиционных систем счисления в настоящее время повсеместно используется десятичная система. Поэтому на записи и чтении чисел в этой системе остановимся более подробно.

Определение 2. Десятичной записью натурального числа х называется его представление в виде

,

где 0 ≤ а_i ≤ 9 (i = 0, 1, ..., п), а_п ≠ 0.

Числа 1, 10, 10², 10³, ..., 10^п называются здесь разрядными единицами, соответственно, первого, второго, третьего и т.д. разрядов.

Три первых разряда в записи числа соединяются в одну группу и называются первым классом, или классом единиц. В первый класс входят единицы, десятки и сотни.

Три следующих разряда – четвертый, пятый и шестой – образуют второй класс, или класс тысяч. В него входят единицы тысяч, десятки тысяч и сотни тысяч.

Затем идет третий класс – класс миллионов. Он также состоит из трех разрядов: седьмого, восьмого, девятого. В него входят миллионы, десятки миллионов и сотни миллионов.

Последующие три разряда – десятый, одиннадцатый и двенадцатый – образуют четвертый класс – класс миллиардов, состоящий из единиц миллиардов, десятков миллиардов и сотен миллиардов.

Следующие три разряда образуют новый класс, и так далее. Единица пятого класса называется триллионом (1 триллион = 1000 миллиардов). Единицы шестого, седьмого, восьмого и т.д. классов (каждая в 1000 раз больше предшествующей) называются, coответственно, квадриллионом, квинтиллионом, секстиллионом, септиллионом, октиллионом и т.д.

Выделение классов создает удобства не только для записи, но и для прочтения чисел. Даются названия первым десяти числам, а затем с помощью небольшого набора новых слов и правил десятичной записи образуются наименования следующих чисел.

Названия чисел второго десятка образуются из соединения первых десяти названий и слова дцать (от слова десять): одиннадцать – один на десять; двенадцать – два на десять; тринадцать – три на десять и т.д. Слово двадцать обозначает два десятка.

Названия чисел третьего десятка образуются из слова двадцать и названий чисел первого десятка: двадцать один, двадцать два, двадцать три и т.д.

Названия чисел четвертого, пятого, шестого, седьмого, восьмого, девятого и десятого десятков образуются по тому же самому правилу, но с добавлением трех новых слов: сорок, девяносто и сто.

Названия чисел второй сотни составляются из слова сто и названий чисел первой сотни: сто один, сто два и т.д., сто девяносто девять. Две сотни кратко называются двести.

Аналогично отсчитываются последующие сотни. Три сотни – триста, четыре сотни – четыреста, пять сотен – пятьсот и т.д. до десяти сотен. Для десяти сотен используется новое слово тысяча. Тысяча тысяч имеет особое название миллион. Тысяча миллионов называется миллиардом (или биллионом).

Для названия всех натуральных чисел в пределах миллиарда оказалось достаточно всего 16-ти различных слов: один, два, три, четыре, пять, шесть, семь, восемь, девять, десять, сорок, девяносто, сто, тысяча, миллион, миллиард. Эти слова являются основными, и все названия остальных чисел до миллиарда получаются из них по описанным выше правилам.

Десятичная запись чисел позволяет достаточно просто решать вопросы, связанные со сравнением натуральных чисел, а также с их сложением, вычитанием, умножением и делением. Поскольку все эти операции изучаются в начальном курсе математики, остановимся на их теоретическом обосновании более подробно.

2. Алгоритм сравнения натуральных чисел вытекает из следующей теоремы.

Теорема 2. Пусть натуральные числа х и у записаны в десятичной системе счисления:

;

.

Число x меньше числа у , если выполнено одно из условий:

а) п < m;

б) п = т, но а_п < b_п;

в) п = m, а_п = b_b, ..., а_i = b_i, но а_i-1 < b_i-1.

Доказательство. а) Пусть п < т. Это означает, что , или. Кроме того,х < 10ⁿ⁺¹ и у ≥ 10^m. Тогда имеем цепочку неравенств х < 10ⁿ⁺¹ ≤ 10^m ≤ y, из которой следует, что х < у.

б) Пусть п = m, но а_п < b_п. Тогда а_п + 1 ≤ b_n. Умножая обе части последнего неравенства на 10^п, получим . Кроме того,и. Следовательно, можем записать цепочку неравенств, из которой опять-таки следует, чтох < у.

Доказательство теоремы для случая в) проводится аналогично.

3. Выведем алгоритм сложения многозначных чисел в десятичной системе счисления. Сначала рассмотрим случай, когда количество цифр в записи чисел х и у одинаково. Пусть

;

.

Тогда, применяя коммутативный и ассоциативный законы сложения, а также дистрибутивный закон умножения относительно сложения, можем записать:

. (9)

Последнюю формулу нельзя рассматривать как десятичное представление числа х + у, поскольку коэффициенты (i = 0, 1, 2, …, n) могут быть больше 9, а значит, операцию сложения нельзя считать законченной. Для завершения сложения выберем наименьший номер i, для которого . Из того, что 0 ≤а_i ≤ 9 и 0 ≤ b_i ≤ 9, следует неравенство 0 ≤ а_i + b_i ≤ 18.

Это означает, что сумму всегда можно представить в виде, где 0 ≤с_i ≤ 9. Тогда , и значит, в равенстве (9) слагаемыемогут быть заменены на.

После этого рассматриваем коэффициенты . Обозначим черезj наименьший номер, для которого (j = i + 1, i + 2,..., n), и повторим описанную выше процедуру. Продолжая этот процесс, не более чем через п шагов мы придем к одному из равенств:

или

,

каждое из которых является десятичной записью натурального числа x + y.

Общий случай, когда в десятичной записи чисел разное количество знаков, легко сводится к рассмотренному дописыванием впереди числа нужного количества нулей.

Из описанного процесса вытекает

Алгоритм сложения многозначных натуральных чисел, представленных в десятичной системе счисления.

1. Записываем второе слагаемое под первым так, чтобы соответствующие разряды находились друг под другом.

2. Складываем однозначные числа разряда единиц. Если их сумма меньше десяти, то записываем ее в разряд единиц ответа и переходим к следующему разряду (десятков).

3. Если же сумма однозначных чисел в разряде единиц больше или равна 10, то представляем ее в виде 10 + с₀, где с₀ – однозначное число, затем записываем с₀ в разряд единиц ответа и прибавляем единицу к числу десятков.

4. Повторяем те же действия с десятками, затем – с сотнями и т.д. Процесс заканчивается, когда будут сложены однозначные числа старших разрядов.

4. Пусть даны два числа – х и у:

;

,

где y < x. Используя свойства операции вычитания, можем записать:

. (10)

Если (i = 0, 1, 2, …, n), то последнее равенство задает алгоритм вычитания.

Если же для некоторых номеровi, то берем наименьшее i, для которого это условие выполняется. Кроме того, предположим, что , но(k > i). Далее воспользуемся равенством:

. (11)

Справедливость равенства (11) легко устанавливается приведением правой части к виду левой.

Используя равенство (11), представление (10) разности x – y можно переписать в следующем виде:

В последнем равенстве все коэффициенты с индексом, меньшим k (будем обозначать их c_j, j = k – 1, …, 1, 0), при соответствующих степенях 10 удовлетворяют неравенствам: 0 ≤ с_j ≤ 9, j = k – 1, ...,1, 0.

Применяя аналогичные преобразования к коэффициентам с номерами, большими или равными k, через п шагов придем к записи равенства (10) в виде:

0 ≤ с_i ≤ 9, i = 0, 1, ..., п.

Из вышеизложенного вытекает

Алгоритм вычитания многозначных натуральных чисел, представленных в десятичной системе счисления.

1. Записываем вычитаемое под уменьшаемым так, чтобы соответствующие разряды находились друг под другом.

2. Вычитание начинаем с разряда единиц. Если число в разряде единиц вычитаемого не превосходит числа в разряде единиц уменьшаемого, то производим вычитание, а затем переходим к следующему разряду.

3. Если же число в разряде единиц вычитаемого превосходит число в разряде единиц уменьшаемого, то занимаем единицу в разряде десятков, увеличивая тем самым число единиц на 10. После этого производим вычитание и переходим к следующему разряду.

4. Если в разряде десятков, сотен и т.д. уменьшаемого записаны нули, то занимаем единицу в первом, отличном от нуля, разряде уменьшаемого, увеличивая тем самым все младшие разряды до единиц на 9, а число разряда единиц – на 10. После этого производим вычитание и переходим к следующему разряду.

5. В следующем разряде повторяем описанный процесс.

6. Процесс вычитания заканчивается, когда будет произведено вычитание из старшего разряда уменьшаемого.

5. Вывод правила умножения многозначных натуральных чисел, записанных в десятичной системе счисления, разобьем на несколько этапов: умножение многозначного числа на однозначное; умножение многозначного числа на числа вида 10^k; умножение многозначного числа на числа вида , где у – однозначное число; умножение многозначного числа на многозначное. Рассмотрим последовательно каждый из этих этапов. Пусть

и у – однозначное число. Тогда

Теперь, используя таблицу умножения, заменим все произведения (i = 0, 1, ..., п) в последнем равенстве соответствующими значениями , где 0 ≤с_i ≤ 9. В результате получаем равенство:

Если в последнем выражении все суммы (i = 0, 1, ..., п) удовлетворяют условию 0 ≤ с_i + b_i ≤ 9, то его можно считать десятичной записью числа х · у. Если же для некоторых сумм выполняются неравенства с_i + b_i ≥ 10, то, представляя их в виде с_i + b_i = 10 + d_i, где 0 ≤ d_i ≤ 9, записывая d_i в соответствующем разряде и прибавляя единицу к следующему разряду, получим десятичную запись числа х · у.

Покажем, что умножение на числа вида 10^k сводится к приписыванию k нулей к десятичной записи числа х.

Действительно,

Последнее выражение является десятичной записью числа .

Рассматривая умножение многозначных чисел на числа вида , гдеу – однозначное число, замечаем, что умножение cводится к последовательному умножению на однозначное число у и на число 10^k. Оба эти приема описаны выше.

Остановимся теперь на умножении многозначного числа на многозначное. Пусть х и у – многозначные числа и

.

Используя дистрибутивный закон умножения относительно сложения, а также ассоциативный закон умножения целых неотрицательных чисел, можем записать:

. Из последнего равенства очевидно, что умножение многозначного числа на многозначное сводится к последовательному умножению многозначного числа х на однозначные числа b_m, b_m-1, …, b₁, b₀, а затем – на числа 10^m, 10^m-1, …, 10, 1. В результате получаем слагаемые, сумма которых является десятичной записью числа х · у.

В общем случае

Алгоритм умножения многозначного числа на многозначное числоможно сформулировать так:

1. Записываем множитель у под множителем х.

2. Умножаем число х на однозначное число b₀, записанное во втором разряде множителя у. Произведение х · b₀ записываем под числом у.

3. Умножаем число х на однозначное число b₁, записанное во втором разряде множителя у. Произведение х · b₁ записываем в следующей строке со сдвигом на один разряд влево, что соответствует умножению х · b₁ на 10.

4. Продолжаем описанный процесс вычислений до тех пор, пока не будет вычислено произведение х · b_т.

5. Полученные m + 1 произведения складываем.

6. Теоретически процесс деления целого неотрицательного числа на натуральное опирается на деление с остатком. Поскольку выполнение действия деления многозначного числа на многозначное в общем виде сопровождается громоздкими вычислениями и связанными с этим трудностями, вывод алгоритма деления рассмотрим на конкретных примерах.

Рассмотрим сначала деление на однозначное число. Деление однозначного и двузначного чисел на однозначное выполняется с помощью таблицы умножения и труда не вызывает. Пусть требуется разделить трехзначное число 356 на 6. Поскольку 60 < 356 < 600, то неполное частное q заключено между числами 10 и 100 и, следовательно, является двузначным числом. Используя таблицу умножения, можно подобрать более точные приближения к числу: 356: 6 · 50 < 356 < 6 · 60 или 300 < 356 < 360. Отсюда следует, что неполное частное q заключено между числами 50 и 60, то есть содержит 5 десятков и имеет вид q = 5 · 10 + a₀. Но тогда должно выполняться неравенство

(50 + а₀) · 6 ≤ 356 < (50 + а₀ + 1) · 6,

или

300 + 6а₀ ≤ 356 < 300 + 6(а₀ + 1).

Из последнего неравенства имеем 6 а₀ ≤ 56 < 6(а₀ + 1).

Пользуясь таблицей умножения, находим, что а₀ = 9 . Значит, неполное частное q = 59. Тогда остаток от деления 356 на 6 равен 356 – 59 · 6 = 2.

Описанный процесс деления коротко представляют следующей записью, которую называют делением «углом».

Аналогично выполняется деление многозначных чисел. В качестве примера рассмотрим деление числа 17325 на 231. Сначала замечаем, что 2310 < 17325 < 23100, а значит, неполное частное является двузначным числом. Цифру десятков находим подбором, последовательно умножая 231 на 10, 20, 30 и т.д., пока не получим число, большее 17325. Иначе говоря, цифру десятков а₁ неполного частного q можно найти из неравенства

231 · 10 · а₁ ≤ 17325 < 231 · 10 · (а₁ + 1),

которое равносильно неравенству

2310 · а₁ ≤ 17325 < 2310 · (а₁ + 1).

Способом подбора находим, что а₁ = 1, поскольку 2310 · 7 = 16170, 2310 · 8 = 18480 и 16170 ≤ 17325 < 18480. Осталось найти цифру единиц а₀ неполного частного q.

Поскольку q = 70 + а₀, то должны выполняться неравенства:

231 · (70 + а₀) ≤ 17325 < 231 · (70 + а₀ + 1),

16170 + 231 · а₀ ≤ 17325 < 16170 + 231 · (а₀ + 1),

231 · а₀ ≤ 1155 < 231 · (а₀ + 1).

Из последнего неравенства опять-таки способом подбора находим а₀ = 5. Итак, частное q = 10 · а₁ + а₀ = 10 · 7 + 5 = 75. Остаток r в этом случае равен нулю, поскольку 17325 – 231 · 75=0. Приведенные рассуждения коротко записывают так:

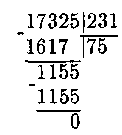
Для общего случая, когда а – произвольное целое неотрицательное число и b – натуральное число, удовлетворяющее условию b ≤ а, можно сформулировать следующий алгоритм деления многозначных чисел.

1. Если а = b, то частное q = 1, остаток r = 0.

2. Если а > b и числа а и b имеют одинаковое число разрядов, то частное q находим подбором, последовательно умножая b на однозначные числа от 1 до 9. Поскольку а < 10 · b, то частное q существует и единственно.

3. Если а > b и число разрядов в числе а больше, чем в b, то выполняем деление «углом». Поиск частного и остатка ведем в следующей последовательности:

а) В числе а выделяем столько старших разрядов, сколько их в числе b, или на один разряд больше, но так, чтобы они образовали первое неполное делимое d₁ ≥ b. Частное q₁ чисел d₁ и b находится подбором при последовательном умножении b на однозначные числа. Записываем q₁ под уголком (ниже b).

б) Умножаем b на q₁ и записываем произведение под числом а так, чтобы младший разряд числа bq₁ был записан под младшим разрядом первого неполного делимого d₁.

в) Находим разность r₁ = d₁ – bq₁.

г) Записываем разность r₁ под числом bq₁ и приписываем справа к r₁ старший разряд из неиспользованных разрядов делимого а. Получаем второе неполное делимое d₂.

д) Если d₂ ≥ b, то относительно него поступаем согласно пунктам 1 и 2. Частное q₂ записываем после q₁.

е) Если d₂ < b, то приписываем к d₂ столько следующих разрядов, сколько необходимо, чтобы получилось число d₃ ≥ b. В этом случае после q₁ записываем столько же нулей.

ж) Относительно неполного делимого d₃ поступаем согласно пунктам 1 и 2. Частное q₂ записываем после нулей. Описанный процесс продолжаем до использования младшего разряда числа а.

з) Если после использования младшего разряда числа а окажется, что d₃ < b, то частное чисел d₃ и b равно нулю. Этот нуль записываем последним разрядом к частному, a d₃ является остатком.

В начальных классах овладение алгоритмом деления идет поэтапно: табличное деление; деление чисел, оканчивающихся нулем; деление двузначного числа на однозначное (сведение внетабличных случаев к табличным); деление двузначного числа на двузначное; деление многозначных чисел на однозначные; деление многозначных чисел на многозначные.