Лекция 3. Позиционные системы счисления, отличные от десятичной План

1. Арифметические операции над систематическими числами.

2. Переход от одной позиционной системы счисления к другой.

Содержание

1. Хотя принятая сейчас во всем мире десятичная позиционная система счисления фактически вытеснила из обихода все остальные системы, тем не менее в науке и технике важную роль играют системы счисления с основаниями, отличными от 10. Так, например, в персональных компьютерах применяются двоичная, восьмеричная и шестнадцатеричная системы записи чисел. Поэтому в настоящем параграфе мы рассмотрим некоторые вопросы, касающиеся систем счисления с произвольным основанием р.

Как уже отмечалось ранее, в системе счисления с основанием р ≥ 2 для записи чисел используются цифры 0, 1, 2, ..., р – 1. Сложение, вычитание, умножение и деление чисел в любой позиционной системе производится аналогично выполнению этих операций в десятичной системе счисления. Для выполнения сложения и вычитания вначале составляется таблица сложения однозначных чисел 0, 1, 2, …, p – 1.

	0	1	2	…	p – 1
0	0	1	2	…	p – 1
1	1	2	3	…	10
2	2	3	4	…	11
…	…	…	…	…	…
p – 1	p – 1	10	11	…

Сложение многозначных чисел в р-ичной системе счисления производится по алгоритму, составленному для сложения многозначных десятичных чисел, с той лишь разницей, что не 10, а р единиц одного разряда образуют единицу следующего разряда.

Слагаемые записываются одно под другим так, чтобы цифры одинаковых разрядов стояли в одной вертикали. Сложение производится по разрядам, начиная с низшего. Результат записывается под горизонтальной чертой, проведенной ниже слагаемых. Если при сложении однозначных чисел в каком-либо разряде суммы получается двузначное число, то в результат записывается лишь последняя цифра, а первая цифра, показывающая число единиц следующего разряда, запоминается и прибавляется к результату сложения чисел этого следующего разряда.

Пример 1.

Аналогично находится сумма большего числа слагаемых.

Пример 2.

Вычитание производится также по разрядам, начиная с низшего. Если в каком-либо разряде уменьшаемого меньше единиц, чем в соответствующем разряде вычитаемого, то из следующего разряда уменьшаемого «занимается» единица, которая представляется как р единиц рассматриваемого разряда. Если же в следующем разряде оказался нуль и «занять» единицу невозможно, то переходим к следующему разряду и «занимаем» единицу там, учитывая что ее можно представить как р – 1 единиц предыдущего разряда плюс рассматриваемого разряда.

Специальной таблицы для вычитания составлять не нужно, так как можно пользоваться таблицей сложения.

Пример 3.

Пример 4.

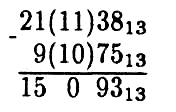
Для выполнения действий умножения и деления в системе счисления с основанием р составляется таблица умножения однозначных чисел.

	0	1	2	…	p – 1
0	0	0	0	…	0
1	0	1	2	…	p – 1
2	0	2	4	…
…	…	…	…	…	…
p – 1	0	p – 1		…

Умножение многозначных чисел производится «столбиком» аналогично умножению в десятичной системе счисления. Первый множитель умножается на число единиц каждого разряда второго множителя с последующим сложением этих промежуточных результатов.

Пример 5.

В промежуточных результатах индекс основания системы не ставится.

Деление в системах с основанием р производится «углом» – так же, как в десятичной системе. При этом используются таблицы сложения и умножения соответствующей системы.

Пример 6.

2. Любое натуральное число х может быть записано в позиционной системе счисления с произвольным основанием р ≥ 2. Поэтому возникает вопрос о переводе записи чисел из одной системы счисления в другую. Для такого перевода можно использовать два способа.

1. Способ деления. Пусть – натуральное число. Для получения его записи в системе с новым основаниемq следует представить его в виде

, (12)

0 ≤ b_i ≤ q – 1 (i = 0, 1, ..., п), b_m ≠ 0, тогда

. (13)

Перепишем равенство (12) следующим образом:

.

Из последней записи очевидно, что b₀ является остатком от деления числа х на основание q новой системы счисления. Неполное частное

представим в виде

.

Из последнего равенства следует, что b₁ в записи 13 числа х является остатком от деления первого неполного частного х₁ на основание q новой системы счисления.

Второе неполное частное х₂ представим в виде

.

Тогда очевидно, что b₂ является остатком от деления второго неполного частного х₂ на основание q новой системы.

Так как неполные частные убывают, то процесс последовательного деления закончится через конечное число шагов, и мы получим неполное частное х_т = b_т, меньшее, чем основание q новой системы.

Таким образом, цифры b_m, b_m-1, ..., b₁, b₀ в записи (13) представляют собой последовательность остатков от деления числа х на новое основание q, записанную в обратном порядке.

Итак, для получения записи числа х в системе счисления с новым основанием q достаточно выполнить последовательное деление числа х на основание q. Последовательность полученных остатков, взятая в обратном порядке, дает нам искомую запись числа х. При этом деление производится в старой системе счисления.

Пример 1. Записать число 5402₈ в пятеричной системе счисления.

Основание новой системы счисления 5 в восьмеричной системе счисления также запишется цифрой 5. Выполним последовательное деление в восьмеричной системе числа 5402₈ на 5. В промежуточных выкладках индекс 8 опускаем.

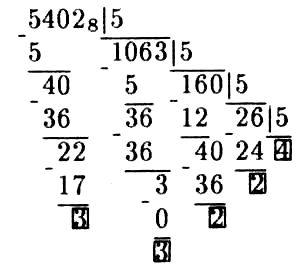
Записывая выделенную последовательность в обратном порядке, получим 5402₈ = 42233₅.

2. Способ умножения. Второй способ перехода от одной системы счисления к другой основан на представлении числа в следующем виде:

.

Для записи числа х в системе с новым основанием q достаточно выполнить последовательно указанные действия в новой системе счисления. Таким образом, а_п умножается на основание р, к результату прибавляется а_п-1. Полученная сумма умножается на р, затем к новому результату прибавляется а_п-2 и т.д. После прибавления а₀ получим число х, записанное в новой системе счисления. Все действия производятся в системе с новым основанием.

Пример 2. Записать число 21012₃ в семеричной системе счисления.

Опуская в промежуточных выкладках индекс 7, можем записать:

В заключение отметим, что оба способа перевода чисел из одной системы счисления в другую теоретически равноценны. Однако практически, когда одна из систем счисления десятичная, способ деления удобнее при переходе из десятичной системы счисления в другую, а способ умножения удобнее при обратном переходе из системы с основанием р в десятичную. В обоих этих случаях выкладки проводятся в привычной для нас десятичной системе.