Первое положение Максвелла:

Переменное во времени электрическое поле приводит к появлению в пространстве магнитного поля.

Запишем (16) в виде проекций:

;

Дифференциальной форме (16) соответствует интегральная форма:

Второе уравнение Максвелла

В результате обобщения многочисленных экспериментальных исследований Фарадей получил закон электромагнитной индукции:

Переменное магнитное поле, пересекающее замкнутый проводящий контур, наводит в этом контуре э.д.с., величина которой пропорциональна скорости изменения потока.

Рисунок 6.5.3 – К иллюстрации закона электромагнитной индукции.

(6.5.17)

Максвелл установил, что причиной возникновения э.д.с. в проводящем контуре является соленоидальное электрическое поле, которое возникает в пространстве и в отсутствие контура. Э.д.с. не зависит от свойств материала, но ток связан с его сопротивлением. Интеграл по замкнутому контуру не равен нулю. Рассмотрим в пространстве некий контур

Рисунок 6.5.4 – К обобщению закона электромагнитной индукции.

поверхность S, на которую опирается этот контур и единичную нормаль – рис.6.5.4. Положительное направление обхода связано с направлением единичной нормали правилом правого винта. Магнитный поток, пересекающий контур, считается положительным или отрицательным в зависимости от того, совпадает он или нет с направлением единичной нормали. Скорость изменения магнитного потока считается положительной или отрицательной в зависимости от того, увеличивается или уменьшается магнитный поток. Запишем обобщения для электромагнитной индукции через вектора электромагнитного поля

.

Магнитный поток, пересекающий поверхность S:

.

Подставляя эти соотношения в выражение (6.5.17), получим:

(6.5.18)

Преобразуем левую часть, используя теорему Стокса

Так как поверхность S и контур L выбраны произвольно, то

(6.5.19)

Выражение (6.5.19) является дифференциальной формой обобщенного закона электромагнитной индукции, а выражение (6.5.18) — его интегральной формой.

Второе положение Максвелла

Переменное магнитное поле возбуждает в пространстве соленоидальное электрическое поле

;

.

6.5.4. Закон Ома в дифференциальной форме

В теле с током выделим элементарный цилиндр. Цилиндр возьмем малым, таким, что в пределах dS распределение тока можно считать равномерным. Его ось совпадает с линиями тока. Ток, протекающий по такому цилиндру, определяется законом Ома: ; где. [R] = [Oм], [] = [ ] .

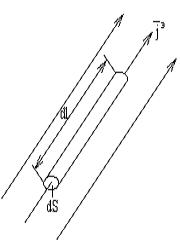
Рисунок 6.5.5 – К пояснению закона Ома в дифференциальной форме.

Известно, что вектор напряженности электрического поля параллелен вектору плотности электрического тока, учитывая, что напряжение между торцами цилиндра ,. Учитывая, что, получаем закон Ома в дифференциальной форме:

—закон Ома в дифференциальной форме

2. 6.5.5. Уточнение понятия о проводниках и диэлектриках

Среды могут существенно отличаться величиной объемной проводимости, поэтому при одной и той же напряженности электрического поля в них могут возбуждаться различные токи. Для удобства классификации сред на проводники и диэлектрики вводят понятия идеального проводника и идеального диэлектрика. Очевидно, что в идеальном проводнике возбуждаются только токи проводимости. Если токи проводимости , то это проводник, а если, ) - диэлектрик. Такая классификация является неоднозначной, так как величина токов существенно зависит от скорости изменения электрического поля.

Рассмотрим гармонически изменяющееся поле . Тогда вектор объемной плотности тока;

;

(6.5.20)

Среды, для которых значение этого отношения значительно больше 1, - называются проводниками ( = 5,75*10⁷ См/м — медь). Среды, для которых значение выражения значительно меньше 1, - называются диэлектриками ( = 2*10^-17 См/м — кварц). Существуют также и промежуточные среды. Например, почва имеет  = 10^-5 См/м, а морская вода —  =5 См/м.

Отметим важную особенность проводящих сред: В области с не может быть постоянным распределение объемного электрического заряда.