77

минимума являются точками излома графика (см. определение 2 лекции 1), в которых производная не существует.

Теорема 2 (Ролля). Пусть функция f (x) :

1)непрерывна на отрезке [a,b];

2)дифференцируема на интервале (a,b) ;

2) f (a) = f (b) .

Тогда существует точка c (a,b) , в которой f ′(c) = 0 (рис. 3).

Рис. 3. Иллюстрация к теореме Ролля

Теорема 3 (Лагранжа). Пусть функция f (x) непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b) . Тогда существует такая точка c (a,b) , что

f (b) − f (a) = f	′	(1)
	(c)(b −a) .

Формула (1) называется формулой Лагранжа или формулой конечных приращений.

Чтобы понять геометрический смысл теоремы Лагранжа, запишем (1) в виде
	f (b) − f (a)		′
		= f	(c) .	(2)
	b −a

Левая часть (2) – это тангенс угла наклона секущей AB (рис. 4), а правая – тангенс угла наклона касательной к графику функции y = f (x) в точке C (c; f (c)).

Рис. 4. Иллюстрация к теореме Лагранжа

Т.о., теорема Лагранжа утверждает, что на интервале (a,b) найдется такая точка c , что касательная к графику в точке C (c; f (c)) будет параллельна секущей AB .

78

Пример 1. Проверим выполнение теоремы Лагранжа для функции y = x2 на отрезке [1,3]. Для этого рассчитаем тангенс угла наклона секущей:

32 −12 = 4 .

3 −1

Производная функции равна y′(x) = 2x , поэтому тангенс угла наклона касательной в точке c равен y′(c) = 2c . Согласно (2), приравняем найденные коэффициенты наклона:

4 = 2c , c = 2 .

Т.о., нашлась внутренняя точка из интервала (1,3), в которой касательная параллельна

секущей.

Найдем уравнения этих прямых. Секущая проходит через точку (1;1) , поэтому ее

уравнение имеет вид:

y −1 = 4(x −1) , y = 4x −3 .

Касательная проходит через точку (2;4) , поэтому ее уравнение: y −4 = 4(x −2) , y = 4x −4 .

Теорема 4 (Коши). Пусть функции f (x) и g(x) непрерывны на отрезке [a,b] и дифференцируемы на интервале (a,b) . Пусть, кроме того, g′(x) ≠ 0 на

(a,b) . Тогда существует точка c (a,b) , что
	f (b) − f (a)	=	f ′(c)	.	(3)
	g(b) − g(a)		′
			g (c)

2. При изучении пределов функций мы рассмотрели несколько способов раскрытия неопределенностей – разложение на линейные множители, умножение и деление на сопряженное, деление на старшую степень переменной и т.п. Основными принято называть

неопределенности вида	0			и		∞
		0				.
						∞

Рассмотрим еще один способ раскрытия основных неопределенностей, который базируется на использовании производной. Он будет изложен в виде теорем, каждую из которых принято называть правилом Лопиталя.

Теорема 5. Пусть функции f (x) и g(x) :

1)дифференцируемы на интервале (a,b) ;

2)lim f (x) = lim g(x) = 0 ;

→x0 x→x0x

′

3) g (x) ≠ 0, x (a,b) ;

4) существует конечный или бесконечный предел lim

f ′(x)

.

x→x0

g (x)

′

Тогда существует предел

lim

f (x)

и при этом выполняется равенство:

g(x)

x→x0

f (x)

0

′

f (x)

lim

=

= lim

.

g(x)

′

0

0

0

x→x

x→x

g (x)

Пример 2. Рассчитаем

2

ln(1+ 2x)

0

(ln(1+ 2x))′

2

1+ 2x

lim

=

= lim

(sin x)′

= lim

= lim

= 2 .

x→0

sin x

0

x→0

x→0

cos x

x→0

cos x(1

+ 2x)

Теорема 6. Пусть функции f (x) и g(x) : 1) дифференцируемы на интервале (a,b) ;

79

2) lim f (x) = ∞ ,	lim g(x) = ∞;
x→x0	x→x0

3) g′(x) ≠ 0, x (a,b) ;

4) существует конечный или бесконечный предел

lim f ′(x) .

x→x0 g′(x)

Тогда существует предел

lim

f (x)

и при этом выполняется равенство:

x→x0

g(x)

f (x)

∞

′

f (x)

lim

=

= lim

.

g(x)

g

′

0

∞

0

x→x

x→x

(x)

Замечание 1. В теоремах 5-6 число x0 может быть как конечным – x0 = C ,

так и бесконечностью

–

x0 = ∞ .

Допускается также, чтобы пределы были

односторонними, т.е. все утверждения остаются верными и при x → x0 ±0 .

Замечание 2. Если производные

f

′

′

(x)

и g (x) удовлетворяют тем же

условиям теорем 5-6, что и исходные функции

f (x)

и g(x) , то эти теоремы

можно применять еще раз:

f (x)

f ′(x)

f ′′(x)

lim

= lim

= lim

.

′

x→x0

g(x)

x→x0

x→x0

′′

g (x)

g (x)

Вообще, эти

теоремы

можно

применять

до

тех

пор,

пока

отношение

производных

f (n) (x)

не

достигнет

конкретного предела

(конечного

или

g(n) (x)

0

∞

бесконечного), т.е. пока не будут преодолены неопределенности

или

.

0

∞

При этом может оказаться так, что предел вообще не будет найден с помощью правила Лопиталя.

Пример 3. Рассчитаем

ln x

∞

(ln x)′

1

2

x

2

x

lim

=

= lim

(

x )′

= lim

= lim

x

= lim

= 0 .

x

x

x→∞

∞

x→∞

x→∞

1

x→∞

x→∞

2

x

Пример 4. Найти lim

xn

, где n – натуральное число.

x→∞ ex

Решение. Имеем

(xn )′

xn

∞

nxn−1

∞

lim

=

= lim

= lim

=

.

(ex )′

ex

x→∞ ex

∞

x→∞

x→∞

∞

Снова

получили неопределенность

∞

(если

n −1 > 0 ).

Применим

правило

Лопиталя

повторно:

∞

lim

nxn−1

= lim

n(n −1)xn−2

.

ex

ex

n −2 > 0 , то

xn−2

→ ∞ и

x→∞

x→∞

Если

правило

Лопиталя

можно

применить

еще раз

и т.д. В

результате получаем цепочку равенств:

xn

= lim

nxn−1

= lim

n(n −1)xn−2

=... = lim

n(n −1) ... 2 1 x0

lim

ex

ex

ex

.

x→∞ ex

x→∞

x→∞

x→∞

Последовательное произведение n натуральных чисел называют n -факториал и обозначают

n! =1 2 ... n .

80

Например, 3! =1 2 3 = 6 . Принято считать, что 0! =1. Возвращаясь к нашему пределу, получим

	xn		n!		C
lim		= lim			=		= 0 .
x→∞ ex		x→∞ ex				∞

3. Правило Лопиталя применимо только для раскрытия основных неопределенностей. Рассмотрим теперь способы раскрытия неопределенностей, не относящихся к основным, а именно:

{0 ∞}, {∞−∞}, {∞0 }, {1∞}, {00 }.

а) Пусть

lim f (x) = 0 ,

lim g(x) = ∞, тогда

x→x0

x→x0

lim [f (x)g(x)]={0 ∞}= lim

f (x)

=

0

1

x→x0

x→x0

0

g(x)

или

g(x)

= ∞

lim [f (x)g(x)]

={0 ∞}= lim

.

1

x→x0

x→x0

∞

f (x)

б) Пусть

lim f (x) = ∞ ,

lim g(x) =∞ , тогда

x→x0

x→x0

1

−

1

lim [f (x) − g(x)]={∞−∞}= lim

g

(x)

f (x)

=

0

.

1

1

x→x0

x→x0

0

f (x)

g(x)

в) Пусть

lim f (x) = lim g(x) = 0 ,

lim g(x) =∞ , тогда

x→x0

x→x0

x→x0

lim [g ( x) ln f ( x)]

{

}

lim [f (x)]

g ( x)

{

0

}

0 ∞

=

0

= e

x→x0

= e

.

x→x0

}

Т.е. неопределенность

{

сводится к неопределенности {0 ∞}, которая, в

00

свою очередь, сводится к

основной способом а). Аналогично раскрываются

{

}

{

}

.

неопределенности ∞0

и 1∞

Пример 5. Найти

lim (x ln x).

x→0+0

Решение. Сведем данную неопределенность к стандартной способом а) и, учитывая замечание 1, применим правило Лопиталя:

ln x

∞

(ln x)′

1

(x ln x)={0 ∞}=

x

lim

lim

=

=

lim

=

lim

1

′

1

x→0+0

x→0+0

∞

x→0+0

1

x→0+0

−

x

x2

x

= lim (−x)= 0 .

x→0+0

81

Лекция 5. ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ

План

1.Производные высших порядков.

2.Монотонность функции.

3.Экстремум функции.

4.Наибольшее и наименьшее значения функции на отрезке.

1. Введем понятие производных высших порядков.

Пусть f ′(x) – производная функции f (x) . Функция f ′(x) называется также первой производной. Производная от f ′(x) называется второй производной функции f (x) и

обозначается f ′′(x) , f (2) (x) или d 2 y . Третьей производной функции f (x) называется dx2

производная от f		′′		f	′′′	(3)	(x)	d 3 y
		(x) , она обозначается			(x) , f			или dx3 . Вообще, n -й производной
от функции	f (x)	называется производная от ее (n −1) -й производной:							f (n) (x) = ( f (n−1) (x))′.
Говорят также, что f (n) (x)			или d n y – это производная порядка n от функции f (x) .
			dxn					(n) (x ) обозначает производную n -го
Если	x – это фиксированная точка, то символ f
	0							0
порядка от функции f (x)			в точке x0 . Для ее существования необходимо существование
производной	f (n−1) (x) не только в точке x , но и в некоторой окрестности этой точки.
				0
Например,		y = xa	– степенная		функция с			произвольным	(не равным нулю)
показателем	a .	Первая производная		y′ = axa−1 .		Если a −1 ≠ 0 , то			вторая производная
y(2) = a(a −1)xa−2 . Если a −2 ≠ 0 , то y(3)				= a(a −1)(a −2)xa−3 и т.д. Таким образом, если a не
является натуральным числом, то n -я производная имеет вид:									(1)
		(xa )(n) = a(a −1)...(a −n +1)xa−n .

Если же a – натуральное число, то формула (1) имеет смысл только для n ≤ a . Рассмотрим подробнее случай, когда a – натуральное число, а порядок производной n = a . В этом случае формула (1) выглядит так:

(xn )(n) = n(n −1)...2 1 = n!.

Для натурального a в случае n > a , очевидно, что n -я производная от xa равна нулю. Пример 1. Пусть y = x4 , тогда

(x4 )′ = 4x3 ,

(x4 )′′ = 4 3x2 =12x2 , (x4 )′′ = 4 3 2x = 24x ,

(x4 )(4) = 4 3 2 1 = 4! = 24 , (x4 )(n) = 0, n > 4 .

Пример 2. Найдем производную порядка n показательной функции y = ax (0 < a ≠1) .

Последовательно дифференцируя, имеем

y′ = ax ln a , y′′ = ax (ln a)2 ,…, y(n) = ax (ln a)n .

В частности, если y = ex , то для любого n имеем

(ex )(n) = ex .

82

2. Важным моментом является применение производной к исследованию возрастания и убывания [зростання і спадання] функции.

Определение 1. Пусть X R – промежуток числовой прямой, т.е. X – это отрезок, либо полуинтервал, либо интервал. Напомним, что функция f (x) называется возрастающей

(убывающей) [зростаючою (спадаючою)] на промежутке X , если для любых x1 , x2 X при x1 < x2 верно неравенство

f (x1 ) < f (x2 ) ( f (x1 ) > f (x2 ) ).

В этом случае

X

–

промежуток монотонности функции. Если в последнем неравенстве

допускается равенство, то функция называется неубывающей (невозрастающей) на X .

Например,

функция,

принимающая постоянное

значение

f (x) = const ,

является

одновременно неубывающей и невозрастающей.

По знаку производной

(«0», «+», «–») можно судить о характере изменения функции

на промежутке ( const , возрастает, убывает).

Теорема

1.

Пусть

функция

f (x) непрерывна

на промежутке X , а ее

производная

′

обращается

тождественно

в

нуль

внутри

X .

Тогда

f (x)

f (x) = const на

X .

Доказательство. Пусть x1 < x2 – две точки на промежутке X . По теореме Лагранжа

найдется точка c (x1 , x2 ) , для которой

′

f (x2 ) − f (x) = f (c)(x2 − x1 ) .

Так как

x1 < c < x2 , то

точка

c

является

внутренней точкой промежутка

X . По

условию

теоремы

′

поэтому

f (x2 ) = f (x1 ) .

Следовательно,

f (x)

принимает

f (c) = 0 ,

постоянное значение на промежутке X .

Теорема

2

(достаточное

условие возрастания и убывания

функции).

Пусть функция

f (x)

непрерывна на промежутке

X , а ее производная

′

f (x) ≥ 0

′

X

и

не обращается тождественно в нуль ни на каком

( f (x) ≤ 0 ) внутри

интервале из промежутка

X . Тогда f (x) возрастает (убывает)

на X .

Доказательство. Приведем доказательство для случая возрастания функции.

Пусть x1 < x2

– две точки из промежутка X . По теореме Лагранжа найдется точка

c (x1 , x2 ) , для которой

′

f (x2 ) − f (x1 ) = f (c)(x2 − x1 ) .

Так как

x1 < c < x2 ,

то точка

c является внутренней точкой промежутка X .

По условию

теоремы

′

поэтому

f (x2 ) ≥ f (x1 ) . Таким образом, мы доказали,

что функция f (x)

f (c) ≥ 0 ,

не убывает на промежутке

X . Следовательно, для любой точки x (x1 , x2 ) выполняются

неравенства f (x1 ) ≤ f (x)

и

f (x) ≤ f (x2 ) . Предположим, что

f (x1 ) = f (x2 ) . Тогда для любой

точки x (x1 , x2 )

имеем

f (x1 ) = f (x) = f (x2 ) , т.е.

f (x) = const на

интервале

(x1 , x2 ) , что

противоречит условию теоремы. Поэтому f (x1 ) < f (x2 ) ,

следовательно

f (x) возрастает на

X .

Для случая убывания функции теорема доказывается аналогично.

Пример 3. Найти интервалы монотонности функции y = x2 −4x +7 .

Решение. Найдем производную функции y′ = 2x −4 . Производная y′ = 2x −4 ≥ 0 при

x ≥ 2 и

y′ = 2x −4 ≤ 0 при

x ≤ 2 . Поэтому функция y = x2 −4x +7

убывает на интервале

(−∞,2] и возрастает на интервале [2;+∞)

(рис. 1).

Пример 4. Найти интервалы монотонности функции y = x −sin x .

83

Решение. Находим производную y′ =1−cos x . Поскольку cos x ≤1 при любом x , то

y′≥ 0 .	Кроме того, производная	y′ =1−cos x обращается в нуль только в изолированных
точках	x = 2πk , k Z . Поэтому	y′ не обращается тождественно в нуль		ни на каком
интервале. Из достаточного условия возрастания функции следует, что				функция y
возрастает на R (рис. 1).

Рис. 1. Графики функций y = x2 −4x +7 (слева) и y = x −sin x (справа)

3. Важным понятием при исследовании функций является экстремум [екстремум] (от лат. extremum – крайний).

Определение 2. Точка x0 называется точкой локального максимума (минимума)

функции f (x) , если для всех x из некоторой окрестности точки x0 выполняется

неравенство (рис. 2):

f (x) ≤ f (x0 ) ( f (x) ≥ f (x0 ))

Рис. 2. Локальный максимум (слева) и минимум (справа)

Локальный (от лат. lokalis – местный) максимум (от лат. maximum – наибольший) и локальный минимум (от лат. minimum – наименьший) объединяются общим названием локальный экстремум. Очевидно, что у функции может быть несколько локальных максимумов и несколько локальных минимумов, причем некоторый локальный максимум может оказаться меньше какого-то локального минимума (рис. 3).

f (x)

84

Теорема 3 (необходимое условие локального экстремума). Для того чтобы дифференцируемая функция имела в точке x0 локальный

экстремум, необходимо чтобы в этой точке выполнялось равенство f ′(x0 ) = 0 . Доказательство. Поскольку x0 – точка экстремума, то существует такой интервал

(x0 −ε, x0 +ε) , на котором f (x0 ) – наибольшее или наименьшее значение. Тогда по теореме Ферма f ′(x0 ) = 0 .

Рис. 3. Функция с несколькими локальными экстремумами

Определение 3. Точки, в которых производная функции обращается в нуль,

называются стационарными.

Из теоремы 3 следует, что точка локального экстремума дифференцируемой функции является стационарной точкой. Обратное утверждение неверно. Рассмотрим, например,

функцию f (x) = x3 . Эта функция возрастает на всей числовой прямой и поэтому не имеет точек локального экстремума. В то же время точка x0 = 0 является стационарной точкой, так как f ′(x0 ) = 3x02 = 0 . То есть необходимое условие локального экстремума в точке x0 = 0

выполняется, но экстремума в ней нет.

Определение 4. Критической точкой функции f (x) называется точка, в которой производная f ′(x0 ) либо равна нулю, либо не существует.

Заметим, что все стационарные точки функции будут и критическими.

Из определения и теоремы Ферма следует, что точка локального экстремума x0 является критической точкой функции f (x) , причем производная в точке x0 может и не существовать. Например, функция y = x имеет в точке x0 = 0 минимум, но не имеет в этой

точке производной (рис. 4, а). Это совсем не означает, что любая точка, в которой функция не имеет производной, обязательно будет точкой локального экстремума. Например,

функция y = 3 x не является дифференцируемой в точке					x = 0 и не имеет в этой точке
экстремум (рис. 4, б). Ее производная имеет вид					0
(3 x )′ = (x1/ 3 )′ = 1 x−2 / 3		=		1	.
3	1			33 x2
Для наглядности построим и график функции y =				(рис. 4, в).
	33 x2

85

Таким образом, если функция имеет в точке локальный экстремум, то она является критической. Обратное утверждение неверно. Другими словами, точки локального экстремума нужно искать среди критических точек. В связи с этим критические точки часто называют точками возможного экстремума или точками, подозрительными на экстремум.

Рассмотрим критерии, позволяющие определять точки максимума и минимума из множества критических точек.

а)	б)						в)
	Рис. 4. Графики функций: а) y =		x		; б) y = 3 x ; в) y =	1
						33 x2
Теорема	4 (достаточное условие локального экстремума). Пусть x0 –

критическая точка функции y = f (x) , которая в этой точке непрерывна,			и пусть
существует окрестность (x0 −ε, x0 +ε)	точки x0 , в которой	функция	имеет
′	самой точки x0 . Тогда:
производную f (x) , кроме, быть может,
1) если при переходе через точку	′	меняет свой знак
	x0 производная f (x)

сплюса на минус, то точка x0 – точка локального максимума функции f (x) ;

2)если – с минуса на плюс, то x0 – точка локального минимума;

3)	если в окрестности		(x0 −ε, x0 +ε) производная имеет постоянный знак,
то x0 не является точкой локального экстремума.
Доказательство. Рассмотрим случай 1). Пусть для некоторого ε > 0								выполняются
условия:	x (x0 −ε	′			′		по теореме		2 на
		, x0 ) : f (x) > 0 ;		x (x0 , x0 +ε) : f (x) < 0 . Тогда
интервале	(x0 −ε, x0 )	функция	f (x) возрастает и		f (x) < f (x0 )	для	всех	x из	этого
интервала, а на интервале (x0 , x0 +ε)				она убывает и	f (x) < f (x0 ) .	Согласно определения 2,

точка x0 – точка локального максимума функции f (x) . Случаи 2) и 3) доказываются аналогично.

Пример 5. Найти точки локального экстремума функции y = x2 −2 x и построить ее

график.

Решение. Запишем нашу функцию в более удобном виде

y= x2 −2x, x ≥ 0x2 +2x, x < 0

Найдем ее производную

2x −2, x > 0 y′ =

2x +2, x < 0

Проверим существование производной в точке x1 = 0 . Вычислим пределы

86

lim	y′ = lim (2x + 2) = 2 ,	lim	y′ = lim (2x −2) = −2 .
x→0−0	x→0−0	x→0−0	x→0+0

Так как левый предел не равен правому, то в точке x1 = 0 производная не существует,

следовательно это критическая точка.

Проверим необходимое условие экстремума. Для этого решим уравнение y′ = 0 и найдем стационарные точки x2 = −1, x3 =1 .

В итоге, найдены три критические точки x1 = 0 , x2 = −1, x3 =1 . Проверим для них первое достаточное условие локального экстремума. При переходе через точку x1 = 0 производная меняет знак с плюса на минус, поэтому x1 = 0 – точка локального максимума. При переходе через x2 = −1, x3 =1 знак производной меняется с минуса на плюс,

следовательно это точки локального максимума. Рассчитаем значения функции в точках локального экстремума y(0) = 0 , y(−1) = −1, y(1) = −1.

Для построения графика функции удобно использовать табл. 1. В первую строку таблицы заносят критические точки и точки разрыва функции. Эти точки разбивают область определения функции на определенное число интервалов, в каждом из которых мы рассчитываем знак производной и определяем характер монотонности функции.

Табл. 1. Вспомогательные сведения для построения графика функции y = x2 −2 x .

	x	(−∞,−1)	−1	(−1,0)	0	(0,1)	1	(1,+∞)
f	′	−	0	+		−	0	+
	(x)
f (x)			−1		0		−1
			min		max		min

С помощью табл. 1 построим на рис. 5 график нашей функции.

Рис. 5. График функции y = x2 −2 x

4. Многие практические задачи формулируются как задачи на нахождение максимального (минимального) значения функции на некотором множестве.

Рассмотрим наиболее простой случай, когда требуется найти наибольшее (наименьшее) значение функции f (x) на отрезке [a,b]. Пусть наибольшее (наименьшее)

значение функции достигается в некоторой точке x0 [a,b]. При этом возможны лишь следующие три случая: 1) x0 = a ; 2) x0 = b ; 3) x0 (a,b) . Пусть x0 (a,b) . Тогда x0 – точка

87

локального экстремума и, если существует f ′(x0 ) , то f ′(x0 ) = 0 . Однако производная f ′(x0 )

может и не существовать.

Предположим, что критические точки функции f (x) на интервале (a,b) образуют конечное множество {x1 , x2 ,..., xn } . Из сказанного выше следует, что точка x0 , в которой функция принимает наибольшее (или наименьшее) значение, совпадает с одной из точек: a,b, x1 ,..., xn . Поэтому для максимального значения функции f (x) на отрезке [a,b] имеем равенство

max[ ] f (x) = max{ f (a), f (b), f (x1 ),..., f (xn )}.

a,b

Аналогично для минимального значения выполняется равенство

min[ ] f (x) = min{ f (a), f (b), f (x1 ),..., f (xn )} .

a,b

Пример 6. Найти наибольшее и наименьшее значение функции f (x) = x2ex на отрезке

[−3,3].

Решение. Имеем f ′(x) = 2xex + x2ex = x(x +2)ex . Критические точки: x1 = 0, x2 = −2 . Наибольшее значение

max f (x) = max{f (−3), f (3), f (0), f (−2)} = max{9e−3 ,9e3 ,0,4e−2 }= 9e3 .

[−3,3]

Наименьшее значение

min f (x) = min{9e−3 ,9e3 ,0,4e−2 }= 0 .

[−3,3]

88

Лекция 6. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ

План

1.Выпуклость кривых.

2.Асимптоты.

3.Схема исследования функции и построение ее графика.

1. Важным свойством функции является монотонность. Однако этого свойства бывает недостаточно, чтобы описать ход изменения функции. На рис. 1 изображены графики функций, которые монотонно возрастают от точки A до точки B . Однако они различны, так как функция, расположенная слева выпукла вниз, а справа – выпукла вверх. Поэтому при построении графиков функций важно знать направление выпуклости кривых.

Рис. 1. Кривые с разным направлением выпуклости

Определение 1. Кривая y = f (x) называется выпуклой вверх (выпуклой вниз) [опуклою

уверх (опуклою униз)] на интервале, если все ее точки, кроме точки касания, лежат ниже (выше) произвольной ее касательной на этом интервале.

Заметим, что для исключения неоднозначности мы не будем употреблять слова «выпуклая» [“опукла”], «вогнутая» [“вгнута”].

Определение 2. Точкой перегиба [перегину] называется точка кривой, в которой график функции меняет направление выпуклости на противоположное.

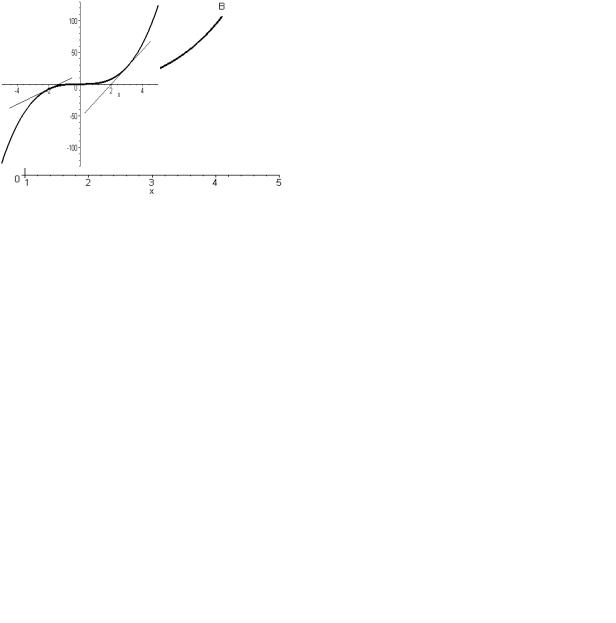
Например, кривая y = x3 (рис. 2) выпукла вверх при x (−∞,0), выпукла вниз при x (0,+∞), а точка (0;0) – точка перегиба.

Рис. 2. График функции y = x3

Интервалы выпуклости находят с помощью следующей теоремы.

										89
Теорема	1. Пусть функция			y = f (x)					дважды дифференцируема на
интервале (a,b). Тогда:
1) если f	′′	на интервале		(a,b), то кривая y = f (x)						выпукла вверх на
	(x) ≤ 0
этом интервале;
2) если f	′′	– выпукла вниз на этом интервале.
	(x) ≥ 0
Например,	функция y = ln x		выпукла			вверх			на всей своей	области определения
D( y) = (0,+∞). Действительно,
			′′	1	′		1
		(ln x) =				= −			< 0 ,
							x	2
				x
следовательно, по теореме 1 кривая			y = ln x		выпукла вверх на всей области определения

(рис. 3).

Примером выпуклой вниз кривой может служить график функции y = 12 x2 +cos x . Ее

вторая производная равна

y′′ = (x −sin x)′ =1−cos x .

Она обращается в нуль в точках x = 2πk, k Z , которые разбивают область определения D( y) = R на счетное число интервалов (2πk,2π(k +1)), k Z . В каждом из этих интервалов

	′′		1	2
y		> 0 , поэтому, согласно теореме 1, кривая	y = 2 x		+cos x выпукла вниз. Следовательно,

кривая выпукла вниз и на всей области определения (рис. 3).

Рис. 3. Графики функций y = ln x (слева) и y = 12 x2 +cos x (справа)

Из теоремы 1 следует, что в точке перегиба вторая производная равна нулю (если она существует). Однако точками перегиба кривой y = f (x) могут быть и точки, в которых

вторая производная f ′′(x) не существует (например, на рис. 4, б) из предыдущей лекции это точка x = 0 кривой y = 3 x ).

Определение 3. Точки, в которых вторая производная f ′′(x) равняется нулю или не существует называют критическими точками второго рода функции f (x) .

Итак, если x0 – абсцисса точки перегиба функции f (x) , то x0 является критической точкой второго рода. Обратное утверждение неверно.