
- •Ю. Н. Полшков
- •СОДЕРЖАНИЕ
- •План
- •План
- •План
- •Рис. 3. Эллипс и его свойства
- •Рис. 4. Гипербола и ее свойства
- •Рис. 5. Парабола и ее свойства
- •Табл. 1. Данные примера 2
- •Молоко
- •Мы уже вводили понятие единичной матрицы
- •Рис. 3. Иллюстрация к теореме Ролля
- •Рис. 4. Иллюстрация к теореме Лагранжа
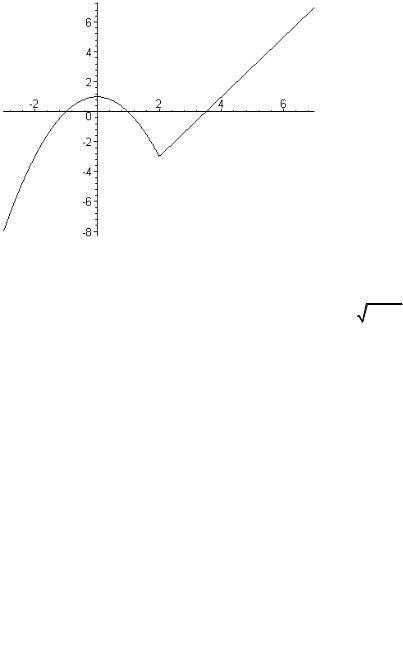
- •Рис. 4.18. График функции
38
Лекция 5. МАТРИЦЫ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
План
1.Матричная запись системы линейных уравнений.
2.Обратная, вырожденная и невырожденная матрицы.
3.Метод Жордана-Гаусса решения матричных уравнений.
4.Решение системы n ×n с помощью обратной матрицы.
1. Одно из важных применений матриц связано с системами линейных уравнений. Рассмотрим систему k ×n
a |
|
x |
+ a |
|
|
x |
2 |
|
+... + a |
|
x |
n |
|
= b |
|
|
|
|
|
|
|
||||||||||
11 1 |
|
12 |
|
|
|
|
|
|
|
1n |
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||
a21 x1 + a22 x2 +... + a2n xn |
= b2 |
|
|
|
|
(1) |
|||||||||||||||||||||||||
............................................ |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
x |
+ a |
k |
2 |
x |
2 |
+ |
... + a |
kn |
x |
n |
|
= b |
k |
|
|
|
|
|
|||||||||||
|
k1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
и соответствующие ей матрицы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a |
|
a |
|
|
|
|
|
|
... |
a |
|
|
|
|
|
|
|
|
|
|
x |
|
b |
|
|
||||||
|
11 |
|
12 |
|
|
|
|
|
|
|
1n |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
||||
a21 |
a22 ... |
a2n |
|
, X |
|
x2 |
|
b2 |
|
|
|||||||||||||||||||||
A = |
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
= |
|
|
, B |
= |
. |
|
||||||||||
... ... ... |
|
|
|
|
|
|
|
|
... |
|
... |
|
|
||||||||||||||||||
a |
k1 |
a |
k 2 |
|
|
|
|
|
... |
a |
kn |
|
|
|
|
|
|
|
|
x |
n |
|
b |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
||||||
Тогда систему (1) можно заменить единственным уравнением |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
AX = B . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
||||||||
Уравнение (2) называют матричной записью системы (1). |
|
|
|||||||||||||||||||||||||||||
Например, система |
|
|
|
|
|
|
3x |
− x |
|
+ 5x |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
3 |
= 4 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2x1 + x2 − 6x3 = 0 |
|
|
|
|
|
|||||||||||||||||||
в матричной записи выглядит так: |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
3 |
|
|
|
|
−1 |
|
|
|
|
|
|
|
1 |
|
|
4 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
x2 |
|
= |
|
. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
− 6 |
|
|
|
|
|
|
0 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
||||
Заметим, что матричную запись систем линейных уравнений применяли |
|||||||||||||||||||||||||||||||
древнекитайские математики во II |
в. до н.э., |
а в европейской науке она применяется с XIX |
|||||||||||||||||||||||||||||
в. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Рассмотрим вопросы, связанные с умножением квадратных матриц порядка n . |
Тогда |
||||||||||||||||||||||||||||||
произведение AB имеет смысл для любых матриц A и B . |
|
|
|
||||||||||||||||||||||||||||
Мы уже вводили понятие единичной матрицы |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 ... |
0 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
1 ... |
0 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
E = |
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
... ... ... |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 ... |
1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
и говорили о том, что для любой квадратной матрицы A выполняется свойство |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
AE = EA = A. |
|
|
|
|
|
|
|
||||||||||||
Известно, что любого числа a ≠ 0 существует обратное число a−1 , для которого |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
aa−1 = a−1a =1. |
|
|
|
|
|
|
|
||||||||||||||
Нечто подобное имеет место и для квадратных матриц, причем роль условия a ≠ 0 |
играет |
||||||||||||||||||||||||||||||
своеобразное условие невырожденности матрицы A . |
|
|
|
|
|
|
|
||||||||||||||||||||||||

39
Определение 1. Пусть A – квадратная матрица порядка n . Квадратная матрица A−1 того же порядка называется обратной для A , если
AA−1 = E .
Для обратных матриц выполняется свойство:
AA−1 = A−1 A = E .
Заметим, что строки матрицы A – это арифметические векторы из Rn , поэтому можно ставить вопрос об их линейной зависимости или независимости.
Определение 2. Квадратная матрица A называется невырожденной, если ее строки линейно независимы, и вырожденной в противном случае.
В лекции 1 мы указывали, что линейно независимая система векторов не может содержать нулевой вектор. Т.о., в невырожденной матрице не может быть нулевых строк.
Над строками матрицы можно совершать элементарные преобразования:
1)переставлять строки;
2)вычеркивать нулевую строку;
3)умножать строку на число c ≠ 0 ;
4)прибавлять к одной из строк другую строку, умноженную на любое число.
Заметим, что речь идет о тех же самых элементарных преобразованиях, которые используются в методе Гаусса, с той лишь разницей, что теперь это строки матрицы, а не уравнения системы.
Теорема 1. Если над строками невырожденной матрицы A проделать элементарные преобразования, то получим снова невырожденную матрицу.
Теорема 2. Для любой невырожденной матрицы A существует обратная матрица A−1 .
3. Рассмотрим матричное уравнение |
|
AX = B , |
(3) |
где A и B – две данные матрицы, X – искомая матрица. Существенно, что A – квадратная |
|
матрица порядка n . В частном случае, когда B = E , искомая матрица |
X будет обратной к |
A , т.е. X = A−1 .
Эффективным методом решения матричных уравнений (3) является метод полного исключения Жордана-Гаусса.
Метод Жордана-Гаусса. Пусть A – невырожденная матрица. Припишем к ней (например, справа) матрицу B и далее будем работать уже со «сдвоенной» матрицей:
(A B).
Если, выполняя элементарные преобразования над строками этой матрицы, привести ее левую часть к единичной матрице E , то правая часть приведется к искомой матрице X . Фактически, метод Жордана-Гаусса можно представить следующей схемой:
(A B)→ (E X ).
В частном случае, когда нужно найти обратную матрицу A−1 , надо совершить переход:
(A E)→ (E A−1 ).
Пример 1. Методом Жордана-Гаусса для матрицы
1 |
1 |
−1 |
|
|
|
3 |
− 2 |
− 4 |
|
A = |
|
|||
|
2 |
3 |
0 |
|
|
|
|||
найти обратную матрицу A−1 .
Решение. Составим «сдвоенную» матрицу
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
1 |
1 |
−1 |
|
1 |
0 |
0 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
(A |
|
E)= 3 |
− 2 |
− 4 |
|
0 |
1 |
0 . |
||
|
||||||||||
|
|
|
2 |
3 |
0 |
|
0 |
0 |
1 |
|
|
|
|
||||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
С помощью элементарных преобразований приведем ее левую часть к единичной матрице
E :
[1] |
1 |
−1 |
|
1 |
0 |
0 |
|
|
|
|
|
1 |
|
|
1 |
|
|
−1 |
|
1 |
|
|
|
0 |
0 |
|
|
|
|
|
1 |
|
|
|
1 |
|
−1 |
|
1 |
|
0 |
0 |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
− 2 |
− 4 |
|
0 |
1 |
0 |
|
→ |
|
0 |
|
|
−5 |
|
−1 |
|
−3 |
|
|
|
1 |
0 |
|
|
|
|
|
0 |
|
|
|
[1] |
|
2 |
|
|
|
− |
2 |
|
0 |
1 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
→ |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
3 |
0 |
|
0 0 1 |
|
|
|
|
|
0 1 |
|
|
|
|
|
2 |
|
|
|
− 2 0 1 |
|
|
|
|
|
0 |
|
|
|
−5 |
−1 |
|
−3 1 0 |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 1 |
−1 |
|
1 0 0 |
|
|
|
|
1 0 |
|
−3 |
|
|
|
3 0 −1 |
|
|
|
|
|
|
|
|
|
−3 |
|
|
|
3 |
|
|
0 |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 0 |
|
|
|
|
|
|
|
−1 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
− |
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
0 1 2 |
|
|
|
− 2 0 1 |
|
→ |
|||||||||||||||||||||||
→ 0 1 |
|
2 0 1 |
0 1 2 |
|
|
− 2 0 1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
−5 |
−1 |
|
− |
3 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
1 |
|
5 |
|
|
||||||||||||||
|
0 |
|
|
|
|
|
0 |
|
|
0 |
|
[9] |
|
|
|
|
|
1 |
|
|
5 |
|
|
|
|
|
0 |
0 |
|
[1] |
|
− |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
9 |
|
|
9 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
− |
12 |
|
|
3 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 0 0 |
9 |
|
|
|
9 |
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
→ |
|
0 1 0 |
|
|
8 |
|
|
|
− |
2 |
|
|
− |
|
1 |
|
|
→ |
|
|
0 1 0 |
|
|
8 |
|
|
|
|
− |
2 |
− |
1 |
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
9 |
|
|
|
9 |
|
|
|
9 |
|
|
|
|
9 |
|
|
|
|
9 |
9 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
0 0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
− |
13 1 |
|
|
|
5 |
|
|
|
|
|
|
|
− |
13 1 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
9 |
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
9 |
|
9 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Правее вертикальной черты получилась обратная матрица A−1 : |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
4 |
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
−1 |
= |
|
|
|
8 |
|
|
|
|
|
|
− |
|
2 |
|
− |
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
9 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
13 |
|
|
|
1 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
9 |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Замечание 1. При нахождении обратной матрицы методом Жордана-Гаусса возможны вычислительные ошибки. Поэтому желательно делать проверку:
AA−1 = E .
4. Рассмотрим произвольную систему n линейных уравнений с n неизвестными:
a x |
+ a x |
2 |
+... + a |
|
x |
n |
= b |
||||||
11 1 |
12 |
|
1n |
|
|
1 |
|||||||
a21 x1 + a22 x2 +... + a2n xn = b2 |
|||||||||||||
............................................ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
x |
+ a |
n2 |
x |
2 |
+... + a |
nn |
x |
n |
= b |
|||
|
n1 1 |
|
|
|
|
|
|
n |
|||||
Запишем эту систему n ×n матричным уравнением
AX = B ,
где
a |
a |
... |
a |
|
|
|
x |
|
|
b |
|
|||
|
11 |
|
12 |
... |
1n |
|
|
1 |
|
|
1 |
|
||
a21 |
a22 |
a2n |
, |
x2 |
|
, |
b2 |
|
||||||
A = |
|
|
|
... |
... |
|
X = |
|
B = |
. |
||||
... ... |
|
|
... |
|
|
... |
|
|||||||
a |
n1 |
a |
n2 |
... |
a |
|
|
|
x |
n |
|
|
b |
|
|
|
|
|
nn |
|
|
|
|
n |
|
||||
Теорема 3. Пусть квадратная матрица A является невырожденной. Тогда решением матричного уравнения
AX = B

41
будет
X = A−1 B .
Доказательство. Используя очевидные преобразования, получим
AX = B A−1 ( AX ) = A−1 B (A−1 A) X = A−1 B EX = A−1 B X = A−1 B .
Теорема доказана.
Замечание 2. Результат, полученный при доказательстве теоремы 3, часто называют
методом обратной матрицы.
Пример 2. Решить систему методом обратной матрицы:
x1 + 2x2 + x3 = 43x1 −5x2 + 3x3 =12x1 + 7x2 − x3 = 8
Решение. Этой системе соответствуют матрицы:
|
1 |
2 |
1 |
|
x |
|
|
|
4 |
||
|
3 |
−5 3 |
|
, |
1 |
|
, |
|
1 |
|
|
A = |
|
X = x2 |
|
B = |
. |
||||||
|
2 |
7 |
|
|
|
|
|
|
|
8 |
|
|
−1 |
|
x3 |
|
|
|
|
||||
Подобно тому, как это делалось в примере 1, найдем обратную матрицу к матрице A :
|
|
|
|
− |
16 |
|
|
3 |
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
33 |
11 |
3 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
A |
−1 |
= |
|
|
|
3 |
|
− |
|
1 |
0 |
|
|
. |
|||||
|
|
11 |
|
11 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
||||||||||
|
|
|
|
31 |
− |
1 |
− |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
33 |
|
11 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|||||||||
Используя теорему 3, получим
|
|
|
|
− |
16 |
|||
|
|
|
|
|
|
|
||
|
|
|
33 |
|||||
|
|
|
|
|
|
|||
X = A |
−1 |
B = |
|
|
|
3 |
|
|
|
|
11 |
|
|||||
|
|
|
|
|||||
|
|
|
|
31 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
33 |
|
||||
|
|
|
|
|
||||
Итак, наша система имеет решение: что оно правильное.
3
11
−111
−111
x1 =1; x2
1 3 4 = 1
0 1 1 .
−1 8 1
3
=1; x3 =1. Проверкой убеждаемся в том,

42
Лекция 6. ОПРЕДЕЛИТЕЛИ
План
1.Определители второго и третьего порядков.
2.Определители порядка n .
3.Свойства определителей.
1. Каждой квадратной матрице A размерности n ×n по определенному закону ставится в соответствие некоторое число ∆A (читается «дельта а»), называемое определителем матрицы A . Т.к. мы условились, что такие матрицы имеют порядок n , то и определитель будет иметь порядок n . Часто вместо слова «определитель» говорят «детерминант». Другие
обозначения определителя – A или det A .
Определитель 2 -го порядка вводится с помощью формулы:
|
|
|
|
|
|
a11 |
a12 |
|
= a |
a |
22 |
− a a |
21 |
, |
(1) |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
a21 |
a22 |
|
11 |
|
12 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
а определитель 3 -го порядка – формулой |
|
|
|
|
|
|
|||||||||
|
a11 |
a12 |
a13 |
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
a21 |
a22 |
a23 |
|
= a11a22 a33 + a12 a23 a31 + a13 a21a32 − a13 a22 a31 − a12 a21a33 − a11a23 a32 . |
||||||||||
|
|
|
|||||||||||||
|
a31 |
a32 |
a33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для запоминания (2) удобно пользоваться схемой: |
|
||||||||||||
+ |
|
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
На левой половине схемы соединены линиями каждые три элемента определителя, произведение которых входит в правую часть (2) со знаком «+». На правой части схемы показаны произведения, входящие со знаком «–».
Для запоминания (2) часто применяют и правило Саррюса. К основному определителю дописывают первые два столбца и действуют по следующей схеме:
Например,
43
|
|
|
|
|
|
2 |
4 |
= 2 (−5) −3 4 = −10 −12 = −22 , |
|
|
|
|
|
|
3 |
−5 |
|
|
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
− 2 |
0 |
|
= 2 (−2) 6 + 3 0 (−1) + 4 1 5 − 4 (−2) (−1) − 2 0 5 −3 1 6 = |
|||
|
−1 |
5 |
6 |
|
|
|
|
|
=−24 −0 + 20 −8 −0 −18 = −30 .
2.Перейдем теперь к общему случаю – рассмотрим определитель порядка n :
|
a11 |
a12 |
... |
a1n |
|
∆A = |
a21 |
a22 |
... |
a2n |
. |
|
... ... ... ... |
|
|||
|
an1 |
an2 |
... |
ann |
|
Определение 1. Минором M ij элемента |
|
aij называется определитель, который |
|||
получается из данного определителя вычеркиванием строки и столбца, содержащих aij .
Алгебраическим дополнением Aij элемента aij называется минор M ij , взятый со знаком
(−1)i+ j , т.е.
A = (−1)i+ j M |
ij |
. |
||||||
ij |
|
|
|
|
|
|||
Например, для определителя |
|
|
|
|
|
|
||
|
|
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|||||
|
|
1 |
− 2 |
0 |
|
|
|
|
|
|
−1 |
5 |
6 |
|
|
|
|
получим, что |
|
|
2 4 |
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
||||
M |
|
= |
=12 + 4 =16 , A = (−1)1+2 |
= −6 . |
|
|||||||||||||||||
|
|
|
22 |
|
−1 |
6 |
|
|
|
|
|
|
|
|
12 |
|
|
−1 |
6 |
|
|
|
Используя понятие алгебраического дополнения, непосредственной проверкой можно |
||||||||||||||||||||||
убедиться в том, что (1) может быть записана, как |
|
|
|
|
|
(3) |
||||||||||||||||
|
|
|
|
|
|
a11 |
|
a12 |
|
= a |
A |
+ a A , |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
a21 |
|
|
|
|
|
11 |
11 |
12 |
12 |
|
|
|
|
|
||
|
|
|
|
|
|
|
a22 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
а (2), как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
a11 |
|
a12 |
a13 |
|
|
|
|
|
|
|
|
|
|
|
(4) |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
a21 |
|
a22 |
a23 |
|
= a11 A11 + a12 A12 |
+ a13 A13 . |
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
a31 |
|
a32 |
a33 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Формулы (3), (4) наводят на мысль о характере общего определения, которое можно |
||||||||||||||||||||||
дать определителю порядка n . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Определение 2. |
Определителем |
матрицы |
A называется сумма |
произведений |
||||||||||||||||||
элементов первой строки на их алгебраические дополнения: |
|
|
|
|||||||||||||||||||
|
a11 |
a12 ... |
a1n |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
∆A = |
a21 |
a22 ... |
a2n |
|
= a11 A11 + a12 A12 |
+... + a1n A1n . |
(5) |
|||||||||||||||
|
... ... ... ... |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
an1 |
an2 ... |
ann |
|
|
|
|
|
|
|
|
|
|
|||||||||
Например, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
44
|
|
|
|
|
0 |
1 |
−1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
0 |
5 |
1 |
|
− 2 |
|
= 0 A +1 A + (−1) A + 2 A = |
|
|
|
|
|||||||||||||||
|
|
|
|
|
−1 |
4 |
0 |
|
|
1 |
|
|
11 |
12 |
|
|
13 |
14 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
3 |
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= 0 (−1)1+1 |
|
5 |
1 |
− 2 |
|
+1 (−1)1+2 |
|
0 |
1 |
− 2 |
|
+ (−1) (−1)1+3 |
|
0 |
5 |
− 2 |
|
+ 2 (−1)1+4 |
|
0 5 |
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
4 |
0 |
1 |
|
|
|
−1 0 |
1 |
|
|
−1 |
4 |
1 |
|
|
−1 |
4 |
0 |
|
= |
||||||||||
|
|
3 |
2 |
3 |
|
|
|
|
|
|
2 |
2 |
3 |
|
|
|
|
2 |
3 |
3 |
|
|
|
2 |
3 |
2 |
|
|
||
|
|
|
|
|
|
|
= 0 +1 (−9) + (−1) 47 + 2 1 = −9 − 47 + 2 = −54 . |
|
|
|
|
|||||||||||||||||||
Заметим, что определение 2 дает и способ вычисления определителей любого порядка. Оказывается, что справедлив и более общий результат.
Теорема 1 (основная теорема об определителях). Определитель равен сумме произведений элементов любой строки на их алгебраические дополнения.
3. Результат, сформулированный как теорема 1, позволяет раскладывать определители порядка n по строке. Это приводит к вычислению ряда миноров, т.е. определителей порядка (n −1) и т.д. Т.о., если n – достаточно большое число, то процедура вычисления может
оказаться громоздкой. Однако, ее можно сильно упростить, если знать свойства определителей.
Основными свойствами определителей являются следующие:
1.Если все элементы некоторой строки равны нулю, то определитель равен нулю.
2.При перестановке двух строк местами знак определителя изменяется на противоположный.
3.Определитель с двумя одинаковыми строками равен нулю.
4.Общий множитель всех элементов строки можно выносить за знак определителя.
5.Если элементы некоторой строки определителя ∆ представлены в виде суммы двух слагаемых, то и сам определитель равен сумме двух определителей ∆1 и ∆2 . В определителе ∆1 указанная строка состоит из первых слагаемых, а в ∆2 – из вторых слагаемых. Остальные строки определителей ∆1 и ∆2 – те же, что и в ∆.
Например,
|
a11 |
|
a12 |
|
a13 |
|
a11 |
a12 |
a13 |
|
a11 |
a12 |
a13 |
|
′ |
′′ |
′ |
′′ |
′ |
′′ |
= |
′ |
′ |
′ |
+ |
′′ |
′′ |
′′ |
. |
a21 |
+ a21 |
a22 |
+ a22 |
a23 |
+ a23 |
a21 |
a22 |
a23 |
a21 |
a22 |
a23 |
|||
a31 |
a32 |
a33 |
|
a31 |
a32 |
a33 |
|
a31 |
a32 |
a33 |
|
|||
6.Если к элементам какой-либо строки прибавить соответствующие элементы другой строки, умноженные на одно и тоже число, то определитель не изменится.
7.Сумма произведений элементов произвольной строки на алгебраические дополнения элементов другой строки равна нулю.
8.Определитель при транспонировании матрицы не изменяется.
Замечание 1. Решение значительно упрощается, если в строке, по которой раскладывается определитель, имеется возможно большее число нулей. Этому можно способствовать, используя свойства определителей.
Замечание 2. Из свойства 8 следует, что любое из свойств определителя остается справедливым, если в формулировках слово «строка» заменить всюду на слово «столбец». В частности, можно сформулировать и аналог теоремы 1.6.
Пример 1. Вычислить определитель матрицы A :
45
5 |
− 2 |
3 |
1 |
|
|
|
|
8 |
2 |
− 4 |
|
10 |
|
||||
A = |
7 |
−3 |
0 |
2 |
. |
|
|
||||
|
1 |
2 |
2 |
−3 |
|
|
|
||||
Решение. Используя свойства определителей и основную теорему 1.6, получим
|
5 |
−2 |
3 |
1 |
|
5 |
−2 |
3 |
1 |
|
−10 −14 0 |
7 |
|
||
|
|
|
|
||||||||||||
∆A = |
10 |
8 |
2 |
−4 |
= 2 |
5 |
4 |
[1] |
−2 |
= 2 |
5 |
4 |
1 |
−2 |
= |
|
7 |
−3 |
0 |
2 |
|
7 |
−3 |
0 |
2 |
|
7 |
−3 |
0 |
2 |
|
|
1 |
2 |
2 |
−3 |
|
1 |
2 |
2 |
−3 |
|
−9 −6 |
0 |
1 |
|
|
= 2 1 (−1)2+3 |
|
−10 |
−14 |
7 |
|
|
|
53 |
28 |
0 |
|
= −2 1 (−1)3+3 |
|
53 |
28 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||
|
7 |
−3 |
2 |
|
= −2 |
|
25 |
9 |
0 |
|
|
= |
||||
|
|
−9 |
−6 |
[1] |
|
|
|
−9 |
− 6 |
1 |
|
|
|
25 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
= −2 (53 9 − 28 25) = −2 (−223) = 446 .

46
Лекция 7. ПРИМЕНЕНИЕ ОПРЕДЕЛИТЕЛЕЙ
План
1.Геометрические применения определителей.
2.Определитель и обратная матрица.
3.Формулы Крамера для системы линейных уравнений n ×n .
1. Рассмотрим два двумерных вектора b = (a11 , a12 ) и c = (a21 , a22 ) . Построим на этих векторах (рис. 1) параллелограмм.
Рис. 1. Параллелограмм, построенный на векторах b и c
Если из координат этих векторов составить матрицу:
a |
a |
|
|
11 |
12 |
|
, |
A = |
|
|
|
a21 |
a22 |
|
|
то ее определитель, взятый по модулю, равен площади параллелограмма, т.е.
S = ∆A .
Рассмотрим теперь три трехмерных вектора b = (a11 , a12 , a13 ) , c = (a21 , a22 , a23 ) , d = (a31 , a32 , a33 ) . Построим на этих векторах (рис. 2) параллелепипед.
Рис. 2. Параллелепипед, построенный на векторах b , c , d
Если из координат этих векторов составить матрицу:
a |
a |
11 |
12 |
A = a21 |
a22 |
|
a32 |
a31 |
a13 a23 , a33
то ее определитель, взятый по модулю, равен объему параллелепипеда, т.е.
V = ∆A .
47
2. Напомним, что квадратную матрицу A мы называли невырожденной, если ее строки линейно независимы, и вырожденной в противном случае. Справедлива следующая теорема.
Теорема 1. Квадратная матрица A невырождена тогда и только тогда, когда ее определитель ∆A не равен нулю.
В лекции 5 был рассмотрен метод Жордана-Гаусса, который позволял найти
обратную матрицу A−1 . Теперь же мы сможем написать и формулу для A−1 . Для краткости рассмотрим матрицу размера 3×3:
a |
a |
a |
|
11 |
12 |
13 |
|
A = a21 |
a22 |
a23 |
. |
|
a32 |
a33 |
|
a31 |
|
Составим матрицу, состоящую из алгебраических дополнений:
|
A |
A |
A |
|
|
11 |
12 |
13 |
|
A* = A21 |
A22 |
A23 |
. |
|
|
A |
A |
A |
|
|
31 |
32 |
33 |
|
Матрицу A * обычно называют присоединенной для A .
Теорема 2. Если ∆A ≠ 0 , то обратная матрица может быть найдена по формуле:
|
|
A−1 = |
1 |
(A *)T . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
||||||||
|
|
∆A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пример 1. Проверить, что матрица |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
A = |
− 2 − 4 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
2 |
|
3 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
является невырожденной, и найти по формуле (1) обратную матрицу A−1 . |
|||||||||||||||||||||||||||||
Решение. Вычислим определитель данной матрицы: |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
∆A = −9 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Т.к. ∆A ≠ 0 , то матрица A является невырожденной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Найдем теперь присоединенную матрицу A * и транспонированную (A *)T : |
|||||||||||||||||||||||||||||
A11 =12; A12 = −8; A13 |
=13; A21 |
= −3; A22 |
= 2; A23 |
= −1; A31 |
= −6; A32 =1; A33 = −5 ; |
||||||||||||||||||||||||
|
12 −8 13 |
|
|
|
|
|
|
|
|
|
|
12 −3 − 6 |
|||||||||||||||||
A* = |
|
−3 2 |
|
−1 |
|
|
|
*)T = |
|
−8 2 |
1 |
|
|||||||||||||||||
|
|
; (A |
|
. |
|||||||||||||||||||||||||
|
|
− 6 1 |
|
−5 |
|
|
|
|
|
|
|
|
|
|
|
13 |
|
−1 −5 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Рассчитаем по формуле (1) обратную матрицу A−1 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
− |
4 |
|
|
1 |
|
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
3 |
|
|
|
||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
A−1 = |
(A *)T = |
|
|
|
8 |
|
|
|
− |
|
2 |
|
− |
1 |
|
. |
|
|||||||||||
|
∆A |
|
|
9 |
|
|
|
9 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
− |
13 |
|
1 |
|
|
5 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
9 |
|
|
9 |
|
|
9 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
В примере 1 лекции 5 мы находили эту же обратную матрицу методом ЖорданаГаусса. Результаты совпали.
3. Рассмотрим произвольную систему n линейных уравнений с n неизвестными:

48
a x |
+ a x |
2 |
+... + a |
|
x |
n |
= b |
||||||
11 1 |
12 |
|
1n |
|
|
1 |
|||||||
a21 x1 + a22 x2 +... + a2n xn = b2 |
|||||||||||||
............................................ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
x |
+ a |
n2 |
x |
2 |
+... + a |
nn |
x |
n |
= b |
|||
|
n1 1 |
|
|
|
|
|
|
n |
|||||
Запишем эту систему n ×n матричным уравнением
AX = B ,
где
a |
a |
... |
a |
|
|
x |
|
|
11 |
12 |
|
1n |
|
1 |
|
|
|
a21 |
a22 |
... |
a2n |
, |
x2 |
|
, |
|
A = |
|
... |
... |
|
X = |
|
||
... ... |
|
|
... |
|
|
|||
|
an2 |
... |
|
|
|
|
|
|
an1 |
ann |
|
xn |
|
|
|||
b1 B = b2 .
...bn
Теорема 3 (правило Крамера). Пусть дана |
система n линейных уравнений с n |
|||||||
неизвестными, записанная матричным уравнением |
AX = B . Если ∆A ≠ 0 , |
то система имеет |
||||||
единственное решение: |
= ∆A1 |
|
|
= ∆A2 ,..., x |
|
|
∆An , |
(2) |
x |
, x |
|
n |
= |
||||
1 |
∆A |
|
2 |
∆A |
|
∆A |
|
|
где Ai означает матрицу, полученную из A заменой i -го столбца столбцом B ( i =1, n ). Пример 2. Решить систему линейных уравнений с помощью правила Крамера
2х1 + х2 + 2х3 =12х1 − х2 + 3х3 =15х1 − х2 + 4х3 = −3
Решение. Запишем данную систему матричным уравнением:
AX = B ,
где
|
|
|
|
|
|
|
|
|
2 1 2 |
x |
|
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
−1 3 |
|
1 |
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
A = |
|
, X = x2 |
, B |
= |
. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
5 |
|
−1 4 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
−3 |
|
|
|||||||
Правило Крамера применимо, если ∆A ≠ 0 . Проверим выполнение этого условия: |
|||||||||||||||||||||||
Составим матрицы Ai , i =1,2,3 : |
|
|
|
|
|
|
∆A =11. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1 |
1 2 |
|
|
2 1 2 |
2 1 |
1 |
||||||||||||
|
|
|
A1 = |
|
1 |
|
−1 3 |
|
|
2 1 3 |
|
|
2 |
|
|
||||||||
|
|
|
|
|
; A2 = |
; A3 |
= |
−1 1 . |
|||||||||||||||
|
|
|
|
|
|
−3 |
−1 4 |
|
|
5 −3 4 |
|
|
5 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
−1 −3 |
|||||||||||||
Их |
определители |
равны: |
|
∆A1 = −22; ∆A2 =11; ∆A3 |
= 22 . |
По |
формулам Крамера (2) |
||||||||||||||||
имеем x = |
|
− 22 |
= −2, x |
2 |
= |
11 |
|
=1, x |
3 |
= |
22 |
= 2 . |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1 |
11 |
|
|
11 |
|
|
|
11 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение данной системы было найдено в примере 3 лекции 2 методом Гаусса. Результаты совпали.
Теорема 4. Однородная система n ×n :
AX = 0
имеет ненулевое решение тогда и только тогда, когда ∆A = 0 , т.е. когда матрица A является вырожденной.

49
ЧАСТЬ I I I МАТЕМАТИЧЕСКИЙ АНАЛИЗ
I I I.а ТЕОРИЯ ПРЕДЕЛОВ
Лекция 1. ПОНЯТИЕ ФУНКЦИИ
План
1.Числовая функция и ее график.
2.Способы задания функции.
3.Понятия обратной и сложной функции.
4.Элементарные функции.
1. Функция – это одно из наиболее важных понятий в математике. В общем смысле ее можно понимать как зависимость между двумя переменными.
Определение 1. Пусть имеются два множества X и Y , и указано правило |
f , по |
||
которому каждому элементу x X |
ставится в соответствие единственный элемент |
y Y . |
|
Тогда говорят, что задано отображение или функция f из X в Y . Множество X |
называют |
||
областью определения функции f |
и обозначают D( f ) = X . Множество Y – |
областью |
|
значений функции f и обозначают E( f ) =Y .
Чаще всего для обозначения функций используют малые латинские ( f , g,h ) или греческие (ϕ,ψ ) буквы. Запись f : X →Y означает, что функция f отображает множество X в множество Y . Для соответствующих элементов x и y используют запись
y = f (x) ,
которая читается «элемент y есть функция f от элемента x ».
В курсе высшей математики изучают числовые функции, которые характеризуются тем, что оба множества X и Y состоят из чисел, т.е. X R,Y R . Независимая переменная
x называется аргументом, а зависимая переменная y – значением функции.
Определение 2. Графиком функции f называют множество точек с координатами
(x, f (x)) , где x X .
Заметим, что каждая прямая, параллельная оси ординат, т.е. каждая прямая x = const (рис. 1), пересекает его либо в единственной точке (если x X ), либо не пересекает вовсе (если x X ).
Рис. 1. Иллюстрация графика функции
50
2. Остановимся теперь на способах задания функции.
Первый способ – табличный. Он используется, когда область определения функции состоит из конечного множества чисел X ={x1 , x2 ,..., xn }. Тогда для задания функции проще
всего указать таблицу
|
|
x |
|
x1 |
|
x2 |
|
|
… |
|
xn |
|
|
||||
|
|
y |
|
y1 |
|
y2 |
|
|
… |
|
yn |
|
|
||||
Например, x – |
производительность труда в усл. |
ед., |
y – прибыль компании в ден. ед. |
||||||||||||||
Данные по этой компании приведены в виде таблицы: |
|
|
|
|
|
|
|
||||||||||
|
|
x |
1 |
|
1,5 |
|
2 |
|
2,5 |
|
3 |
|
|||||
|
|
y |
2,4 |
|
2,31 |
|
2,93 |
|
3,57 |
|
3,1 |
|
|||||
Ее график изображен на рис. 2.
Рис. 2. График функции, заданной табличным способом
Второй способ задания функции – аналитический. При этом способе указывают
формулу, с помощью которой связаны переменные x и y . Например, y = x2 +1 , y = sin 2x и т.п. Функция может задаваться и с помощью нескольких формул (рис. 3):
−x2 +1, x < 2 y =
2x −7, x ≥ 2
Рис. 3. График функции, заданной аналитическим способом

51
Третий способ задания функции – графический, т.е. с помощью графика (рис. 4). Его часто используют для практических целей. Это может быть, например, траектория ракеты, электрокардиограмма и т.п.
Рис. 4. График функции, заданной графическим способом
3. Над функциями можно совершать различные математические операции: сложение, умножение и т.д. Подробно рассмотрим операции построения обратной и сложной функций.
Пусть |
имеется |
функция y = f (x) |
с D( f ) = X |
и |
E( f ) =Y . Предположим |
|
дополнительно, что разным значениям x отвечают разные значения y : |
||||||
|
|
x1 ≠ x2 y1 ≠ y2 . |
|
(1) |
||
Заметим, что не каждая функция удовлетворяет этому требованию. Например, для |
||||||
функции y = x2 |
разным числам x и (−x) соответствует одно число x2 . |
|||||
Итак, если выполняется условие (1), то для каждого |
y Y |
существует только одно |
||||
значение x X , такое, |
что f (x) = y . |
Такое отображение множества Y в множество X |
||||
называется обратным к отображению f |
и обозначается f −1 : |
|
|
|||
|
|
f : X →Y , |
f −1 :Y → X . |
|
|
|
Т.о., обратная функция для y = f (x) есть x = f −1 ( y) . Т.к. буквой x обозначают аргумент, а значение функции – буквой y , то обратная функция запишется обычным образом:
|
y = f −1 (x) . |
|
|
|
Пример |
1. Пусть y = x2 . У этой функции D( y) = R , |
E( y) =[0,+∞) . Формально |
||
обратной функции не существует, т.к. x = ± |
y . Если же принять D( y) =[0,+∞) , то будем |
|||
иметь x = y . |
Меняя обозначения, получим запись обратной |
функции в виде |
y = x . |
|
Обратной функцией к y = 2x будет функция |
y = log2 (x) . Графики этих взаимно обратных |
|||
функций изображены на рис. 5. |
|
|
|
|
Заметим, |
что графики исходной функции y = f (x) и обратной y = f −1 (x) |
всегда |
||
симметричны относительно «биссектрисы» 1-й и 3-й координатных четвертей, т.е. относительно прямой y = x (см. рис. 5).
Другой важной операцией является построение сложной функции. Рассмотрим две функции: x = h(t) с D(h) =T , E(h) = X ; y = g(x) с D(g) = X , E(g) =Y . Тогда схема:
t h →x g → y
определяет новую функцию с областью определения T и областью значений Y . Эта новая функция обозначается
y = g(h(t))

52
и называется сложной функцией. Заметим, что в определении этой сложной функции участвовали две функции h и g . Поэтому данную сложную функцию называют
композицией двух функций h и g .
Рис. 5. Графики взаимно обратных функций y = x2 и y = |
x (слева), |
y = 2x и y = log2 (x) |
|
(справа) |
|
|
|
Например, композиция двух функций |
y = ln x и |
x = 2t −1 |
определяет сложную |
функцию y = ln(2t −1) . Ее область определения |
D( y) определяется решением неравенства |
||
2t −1 > 0 , т.е. D( y) = (0,5;+∞) . |
|
|
|
4.В рамках школьной математики были изучены основные функции. К ним относятся:
1)Степенные функции
y = xa ,
где a – любое действительное постоянное число (рис. 6). Областью определения считается промежуток x > 0 . Однако, если a – натуральное число, то D( y) = R .
y = x3 |
|
y = x4 |
y = x1/ 3 |
y = xπ |
|
|
|
|
Рис. 6. Графики степенных функций |
|
|
2) |
Показательные функции |
y = ax , |
|
||
|
|
|
|
|
|
где a > 0 |
, a ≠1 |
, |
D( y) = R (рис. 7). |
|
|
3) |
Логарифмические функции |
y = loga x , |
|
||
где a > 0 |
, a ≠1 |
, |
D( y) = (0,+∞) (рис. 7). |
|
|
|
|
||||

53
y = ex |
y = (0,5)x |
y = log3 x |
y = log0,2 x |
Рис. 7. Графики показательных и логарифмических функций
4) Тригонометрические функции (рис. 8)
y = sin x , y = cos x , y = tg x , y = ctg x .
y = sin x |
y = cos x |
y = tg x |
y = ctg x |
Рис. 8. Графики тригонометрических функций
5) Обратные тригонометрические функции (рис. 9)
y = arcsin x , y = arccos x , y = arctg x , y = arcctg x .
Для первых двух функций – D( y) =[−1,1] , для остальных – D( y) = R .
y = arcsin x |
y = arccos x |
y = arctg x |
y = arcctg x |
Рис. 9. Графики обратных тригонометрических функций
Основные функции перечислены. Укажем теперь допустимые действия над ними:
1)все арифметические действия: f + g, f − g, f g, gf ;
2)построение сложной функции.
Определение 3. Элементарными функциями называются основные функции и полученные из них с помощью допустимых действий.
Например, элементарными функциями являются y = 1−ln x , y = arccos(1−ex ) и т.п.
Заметим, что в указанных примерах областью определения функции можно считать ОДЗ или часть ОДЗ.

54
Лекция 2. ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
План
1.Числовая последовательность и ее предел.
2.Свойства и правила нахождения пределов последовательностей.
3.Бесконечно малые и бесконечно большие последовательности. Число e .
1. Важным понятием высшей математики является понятие предела числовой последовательности.
Определение 1. Числовой последовательностью называется числовая функция,
определенная на множестве натуральных чисел. |
– задать отображение n → x(n), |
|
|||||
Задать числовую последовательность значит |
т.е. |
||||||
бесконечный ряд чисел |
|
|
|
|
|
|
|
x1 = x(1), x2 = x(2), x3 = x(3), … |
|
||||||
Числовую последовательность с членами x1 , x2 , … |
записывают коротко {xn }, n N , |
или |
|||||
просто {xn }. |
называется пределом последовательности {xn }, если для |
||||||
Определение 2. Число a |
|||||||
любого положительного числа ε |
существует такой номер n0 (зависящий, вообще говоря, от |
||||||
выбранного ε ), начиная с которого все члены последовательности отличаются от a |
по |
||||||
модулю меньше, чем на ε , т.е. |
|
|
|
|
|
|
|
ε > 0 n0 : n ≥ n0 |
|
xn −a |
|
< ε . |
|
||
|
|
|
|||||
Если последовательность {xn }имеет предел a , то она называется сходящейся к числу |
|||||||
a , и мы пишем |
|
|
|
|
|
|
|
lim x = a , |
или |
x → a при n →∞. |
|
||||
n→∞ n |
|
|
|
n |
|
||
Т.о., последнее равенство означает, что как бы то ни было мало положительное числоε , все члены последовательности, начиная с некоторого номера n0 , удовлетворяют
неравенству xn −a <ε . Проще говоря, числа xn с ростом n неограниченно приближаются к a .
Множество всех чисел x , удовлетворяющих условию xn −a <ε (где ε > 0 ), называется ε -окрестностью точки a . Это множество – интервал (a −ε,a +ε). Неравенство xn −a < ε означает, что какова бы ни была окрестность точки a , найдется такой номер n0 ,
начиная с которого все члены последовательности будут содержаться в этой окрестности. Следовательно, вне ε -окрестности может находиться лишь конечное число членов последовательности.
|
Пример 1. Рассмотрим последовательность 1, |
1 |
, 1 |
,..., для которой |
xn |
= |
1 |
(n =1,2,...). |
|
|
2 |
3 |
|
|
|
n |
|
Числа |
x неограниченно приближаются к 0, поэтому естественно ожидать, |
что lim 1 = 0 . |
||||||
|
n |
|
|
|
|
|
|
n→∞ n |
|
|
|
|
|
|
|
|
|
Проверим, что такое предположение согласуется с формальным определением предела.
Возьмем любое ε > 0 (например, ε = 0,001). Неравенство |
|
|
x −0 |
|
<ε , или 1 |
<ε , выполняется |
||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
n |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
для всех n > |
1 . Поэтому приняв за n |
ближайшее к 1 справа целое число (в нашем примере |
||||||||||||
|
ε |
0 |
|
ε |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
n =1001), мы будем иметь для всех n ≥ n |
неравенство |
|
x |
−0 |
|
<ε , следовательно, lim x = 0 . |
||||||||
|
|
|||||||||||||
0 |
|
|
0 |
|
|
n |
|
|
|
|
|
n→∞ n |
||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
55 |
|
|
Пример 2. Пусть |
x |
|
|
= n −1 |
( n N ), |
покажем, |
что lim x =1 . Взяв произвольное |
||||||||||
|
|
|
|
|
|
|
n |
|
|
n +1 |
|
|
|
|
n→∞ n |
||||
ε > 0 , составим неравенство |
|
xn −1 |
|
<ε |
и выясним, для каких n оно справедливо. Имеем: |
||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
n −1 |
−1 |
|
<ε |
2 |
|
<ε |
n +1 > 2 |
n > 2 −1. |
||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
n +1 |
|||||||||||||
|
|
|
|
|
n +1 |
|
|
|
|
|
|
|
|
ε |
ε |
||||
Таким образом, приняв за |
n |
|
|
ближайшее к 2 −1 справа положительное целое число, будем |
|||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
иметь |
|
x −1 |
|
< ε для всех n ≥ n , что означает справедливость равенства lim x =1 . |
|||||||||||||||
|
|
||||||||||||||||||
|
|
n |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
n→∞ n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2.К свойствам пределов последовательностей относятся следующие:
1.Сходящаяся последовательность имеет только один предел.
2.Сходящаяся последовательность всегда ограничена.
|
|
|
3. |
Если |
|
члены сходящейся последовательности {xn } |
удовлетворяют неравенству |
||||||||||||
x |
≥ b , то и lim x ≥ b . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
n |
|
|
|
n→∞ n |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
4. |
Если члены сходящихся последовательностей {xn } |
и {yn} связаны неравенством |
||||||||||||||
x |
≥ y |
n |
( n =1,2,... ), то lim x ≥ lim y |
n |
. |
|
|
|
|
|
|
||||||||
n |
|
|
|
|
|
n→∞ |
n |
n→∞ |
|
|
|
|
|
|
|
||||
|
|
|
5. |
Если члены сходящихся трех последовательностей {xn }, {yn} |
и {zn} связаны |
||||||||||||||
неравенством |
xn ≤ yn ≤ zn |
( n =1,2,... ) и при этом последовательности |
{xn } и {zn} |
имеют |
|||||||||||||||
один и тот же предел a , то и lim yn |
|
= a . |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
||
|
|
|
Заметим, что свойство 5 часто называют «леммой о двух милиционерах» |
|
|||||||||||||||
|
|
|
Кроме рассмотренных выше свойств, имеется несколько правил, постоянно |
||||||||||||||||
применяемых при нахождении пределов. |
|
|
|
|
|
|
|||||||||||||
|
|
|
Пусть lim x = a и lim y |
n |
= b . Тогда: |
|
|
|
|
|
|
||||||||
|
|
|
|
|
n→∞ n |
n→∞ |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1. |
lim(xn + yn )= a +b |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(словами: «предел суммы равен сумме пределов»); |
|
|
|
|
|
|
|||||||||||||
|
|
|
2. |
lim(xn yn )= a b |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(словами: «предел произведения равен произведению пределов»); |
|
|
|
|
|
||||||||||||||
|
|
|
3. |
lim |
1 |
|
= 1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
если все числа yn , а также и сам предел b , отличны от нуля; |
|
|
|
|
|
|
|||||||||||||
|
|
|
4. |
lim |
xn |
|
= a , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
если все yn , а такжеb , не равны нулю. |
|
|
|
|
|
|
|||||||||||||
3. Рассмотрим еще некоторые важные понятия. |
|
|
|
|
|
|
|||||||||||||
|
|
|
Определение 3. Последовательность {xn } называется бесконечно |
малой, если ее |
|||||||||||||||
предел равен нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Для бесконечно малых последовательностей при вычислении пределов часто |
||||||||||||||||
применяют обозначение |
{0}. |
Например, последовательности вида |
x = |
|
1 |
, при |
k > 0 |
||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
nk |
|
|
являются бесконечно малыми.

56
Определение 4. Говорят, что последовательность {xn }имеет своим пределом +∞, если для любого (сколь угодно большого) числа A > 0 существует такой номер n0 , начиная с которого все числа xn больше A :
A > 0 n0 : n ≥ n0 xn > A .
В этом случае пишут: lim x = +∞. |
|
|
|
|
|
x→∞ n |
|
|
|
|
|
Например, каждая последовательностей |
|
|
|
|
|
|
|
n |
2 |
|
|
{ |
n},{n},{n2}, |
|
|
|
|
|
|
|
|||
|
n + |
1 |
|||
имеет пределом +∞.
Аналогично определяется предел −∞: запись lim xn = −∞ означает, что
x→∞
A > 0 n0 : n ≥ n0 xn < −A .
Определение 5. Если предел последовательности равен +∞ или −∞, то ее называют
бесконечно большой.
Для бесконечно больших последовательностей при вычислении пределов часто применяют обозначение {∞}.
Пусть C – положительная константа. Тогда при осуществлении предельного перехода справедливы равенства:
{C∞} = 0 и {0}C = ∞ .
Рассмотрим последовательность, состоящую из чисел
|
+ |
1 n |
|
xn = 1 |
|
,n =1,2,.... |
|
|
|
n |
|
Следующая таблица дает представление о некоторых из чисел xn :
n |
1 |
2 |
3 |
4 |
5 |
10 |
100 |
1000 |
10000 |
xn |
2 |
2,25 |
≈2,37 |
≈2,44 |
≈2,49 |
≈2,59 |
≈2,7 |
≈2,717 |
≈2,718 |
Видно, что числа xn растут, но этот рост постепенно замедляется. Последовательность {xn } сходится к основанию натурального логарифма, т.е. числу e ≈ 2,718281828 .
Определение 6. Числом e называется предел
|
+ |
1 n |
lim 1 |
. |
|
n→∞ |
|
n |

57
Лекция 3. ПРЕДЕЛ ФУНКЦИИ
План
1.Определение предела функции.
2.Свойства и правила нахождения пределов функций.
3.Бесконечно малые и бесконечно большие функции.
4.Замечательные пределы. Сравнение функций. Эквивалентные функции.
1. Прежде чем дать понятие предела функции, введем необходимые термины.
Пусть функция f (x) определена в некоторой окрестности точки x0 , исключая, быть может, саму точку x0 . Окрестность (x0 −ε; x0 +ε ) точки x0 , из которой исключена сама
точка |
|
x0 , |
|
т.е. фактически |
множество |
(x0 −ε; x0 ) (x0 ; x0 +ε ), |
|
|
назовем |
проколотой |
||||||||||||||||||||||||||||
окрестностью точки x0 или ε -окрестностью точки x0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
Определение 1. Пусть функция |
f (x)определена в некоторой ε -окрестности точки |
||||||||||||||||||||||||||||||||||
|
x0 , за исключением быть может самой точки x0 . Говорят, что число |
A является пределом |
||||||||||||||||||||||||||||||||||||
функции f |
( |
x |
) |
0 |
|
|
|
|
|
f |
( |
x |
) |
|
0 |
|
|
x→x |
( |
x |
) |
= A), если для любого |
||||||||||||||||
|
|
|
при x → x (пишут |
|
|
→ A при x → x |
или lim f |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||
ε > 0 |
|
существует зависящее от ε |
число δ > 0 такое, что |
|
f (x)− A |
|
<ε при |
0 < |
|
x − x0 |
|
<δ |
||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||
(рис. 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Аналогично lim f (x)= A , если для всякого ε > 0 |
существует зависящее от ε число |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
N такое, что |
|
f (x)− A |
|
<ε при |
|
|
x |
|
> N . Употребляется также запись |
lim f (x)= ∞, которая |
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
обозначает, что для всякого числа |
|
B > 0 |
существует зависящее от B число δ такое, что |
|||||||||||||||||||||||||||||||||||
|
f (x) |
|
> B при 0 < |
|
x − x0 |
|
<δ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Рис. 1. Иллюстрация понятия предела функции |
|||||||
Пример 1. lim |
3x2 |
− x −2 |
= |
12 −2 −2 |
= |
8 |
. |
|
2x2 |
+ x −3 |
8 +2 −3 |
7 |
|||||
x→2 |
|
|
|
|||||
Такой метод решения иногда называют метод непосредственной подстановки.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
58 |
|
Если x → x0 |
и при этом x < x0 , то пишут x → x0 −0 ; аналогично, если x → x0 |
и при |
|||||||||||||||||
0 |
0 |
f |
( |
0 |
) |
= |
x→x −0 |
( |
x |
) |
и f |
( 0 |
) |
= |
x→x +0 |
( |
x |
) |
|
этом x > x , то пишут x → x +0 . Числа |
|
x −0 |
|
lim f |
|
|
x +0 |
|
lim |
f |
|
|
|||||||
|
|
|
|
|
|
|
0 |
|
|
|
f (x) |
|
|
|
0 |
|
|
|
|
называются соответственно пределом слева |
и справа |
функции |
|
в точке |
x0 . |
Такие |
|||||||||||||
пределы называют односторонними (левосторонними и правосторонними, соответственно).
Для существования предела функции f (x) при x → x0 необходимо и достаточно, чтобы выполнялось равенство f (x0 −0)= f (x0 +0).
2. Свойства и правила нахождения пределов функций аналогичны тем, что приводились для пределов последовательностей. Приведем лишь некоторые из них.
Пусть существуют пределы
Тогда:
1. lim (f (x)+ g (x))= a +b ;
x→x0
2. lim (f (x) g (x))= a b ;
x→x0
3. |
lim |
1 |
= |
1 |
, если g (x)≠ 0 |
|
g (x) |
b |
|||||
|
x→x0 |
|
|
|||
|
|
|
|
|
||
4. |
lim |
f (x) |
= a |
, если g (x)≠ 0 |
||
g (x) |
||||||
|
x→x0 |
|
b |
|
||
|
|
|
|
|
||
Пример 2. lim 3x2 − x −2
x→1 2x2 + x −3
|
3lim |
|
2 |
|
|
3 |
|
5 |
|
|
|
|
|
x + |
3 |
|
|
|
5 |
|
|||||
= |
x→1 |
|
|
= |
|
|
3 |
= |
=1. |
|||
2lim |
|
3 |
2 |
|
5 |
5 |
||||||
|
|
|
|
|||||||||
|
x + |
2 |
|
|
2 |
|
|
|
||||
|
x→1 |
|
|
|
|
|
|
|
|
|||
lim f (x)= a и lim g (x)= b . |
|
x→x0 |
x→x0 |
вокрестности x0 , а также b ≠ 0 .
вокрестности x0 , а также b ≠ 0 .
|
|
|
|
|
|
|
|
3 |
|
2 |
|
(x −1) |
|
3 |
|
2 |
|
|
3 |
−1−2 |
0 |
|
|
x + |
3 |
|
|
x + |
3 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
= |
|
|
|
= |
|
|
= lim |
|
|
= lim |
|
= |
||||||
2 |
+1−3 |
0 |
|
|
3 |
|
|
|
3 |
|||||||||
|
|
|
x→1 |
2 |
(x −1) |
x→1 |
2 |
|
||||||||||
|
|
|
|
|
|
|
|
x + |
2 |
|
|
x + |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Символ |
0 |
|
принято называть неопределенностью ноль делить на ноль. Данная |
||
|
|
|
|||
0 |
|||||
|
|
|
|
||
неопределенность раскрывается с помощью метода разложения многочленов на линейные множители.
3. Систематизируем наши знания о пределах. |
|
|
|
|
|
|||||
x→x |
( |
Определение 2. Функция |
f (x) называется |
бесконечно малой при x → x0 , если |
||||||
x |
) |
|
0 |
x→x |
( |
x |
) |
= ±∞ . |
||
lim f |
|
|
= 0 , и бесконечно большой при x → x , если lim f |
|
|
|||||
0 |
|
|
|
|
|
0 |
|
|
|
|
Справедливы следующие две теоремы.
Теорема 1. Сумма и произведение двух бесконечно малых функций (при x → x0 ) снова являются бесконечно малыми функциями (при x → x0 ).
Теорема 2. Произведение бесконечно малой функции на ограниченную функцию есть снова бесконечно малая функция.
В следующем примере будет рассмотрено отношение бесконечно малых функций и применен метод домножения на выражение, сопряженное иррациональному.

59
|
|
|
x2 − x −6 |
0 |
|
|
|
|
|
|
(x +2)(x −3)( |
x +3 +1) |
|
|
|
|
||||||
|
Пример 3. lim |
|
|
|
= |
|
= lim |
|
|
|
|
|
|
= |
|
|
|
|||||
|
|
|
( |
|
|
)( |
) |
|
|
|
||||||||||||
|
|
x→−2 |
x +3 −1 0 |
|
x→−2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
x +3 −1 |
x +3 +1 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= lim |
(x +2)(x −3) ( x +3 +1) |
= lim (x |
−3) |
( |
x |
+3 +1 = −10 . |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
x +2 |
|
|
|
|
|
||||||||||||||||
x→−2 |
|
|
|
x→−2 |
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|||
|
Теорема 3. Величина, обратная бесконечно малой, является бесконечно большой. И |
|||||||||||||||||||||
наоборот, величина, обратная бесконечно большой, является бесконечно малой. |
|
|
|
|||||||||||||||||||
|
Т.о., |
если lim f (x)= 0 , |
то |
lim |
|
|
1 |
|
|
= ∞ . И, если lim f (x)= ±∞ , то |
lim |
1 |
= 0 . |
|||||||||
|
|
f |
(x) |
f (x) |
||||||||||||||||||
|
|
x→x0 |
|
|
|
|
x→x0 |
|
|
|
x→x0 |
|
x→x0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|||
Символически это записывают так: |
|
|
|
= ∞ |
и |
|
= 0 . |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
∞ |
|
|
|
|
|
|
|||
Имеет место и более общий результат. Для любого действительного числа a > 0 при предельном переходе выполняется следующее:
a |
|
a |
|
a |
|
a |
|
|
a |
|
a |
|
||||||||
|
|
|
= +∞; |
|
|
= −∞; |
|
= ∞; |
|
|
= 0 |
; |
|
|
= −0 |
; |
|
|
= 0 . |
|
|
−0 |
|
|
|
||||||||||||||||
|
+0 |
|
|
|
|
0 |
|
+∞ |
|
|
−∞ |
|
|
∞ |
|
|||||
Символы {+0} |
|
и {−0} |
означают, |
|
соответственно, |
бесконечно малые функции |
||||||||||||||
положительного и отрицательного знака.
В следующем примере рассмотрим отношение бесконечно больших функций и изучим метод деления на старшую степень неизвестного.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x2 |
|
x |
|
|
2 |
|
|
|
|
1 |
|
2 |
|
||||
|
|
|
|
|
|
3x2 |
− x −2 |
|
|
∞ |
|
|
2 − |
|
|
|
− |
|
|
|
|
|
3 − |
|
− |
|
|
|
||||
|
|
Пример 4. lim |
|
|
x |
x |
2 |
x |
2 |
x |
x |
2 |
|
|||||||||||||||||||
|
|
|
|
|
= |
|
|
= lim |
|
|
|
|
|
|
|
|
= lim |
|
|
|
= |
|||||||||||
|
|
2x2 |
+ x −3 |
|
2x2 |
|
x |
|
|
3 |
|
|
|
1 |
|
3 |
||||||||||||||||
|
|
|
|
x→∞ |
|
|
∞ |
x→∞ |
+ |
|
− |
|
|
x→∞ 2 + |
− |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
x2 |
|
|||||||||||||||||||
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
x2 |
x2 |
|
x2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
lim 3 −lim |
−lim |
|
|
3 −0 −0 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
x→∞ |
x→∞ x |
x→∞ x2 |
|
= |
= |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
lim 2 +lim |
1 |
−lim |
3 |
|
2 +0 −0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x→∞ |
x→∞ x |
x→∞ x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4. В математическом анализе есть пределы особой важности. Их называют замечательными.
Первый замечательный предел:
Второй замечательный предел:
или в виде функции
lim 1+
x→∞
|
lim sin x |
=1. |
|
|||
|
x→0 |
|
x |
|
|
|
|
|
|
+ |
1 n |
|
|
lim 1 |
|
= e , |
|
|||
n→∞ |
|
n |
|
|
||
1 |
x |
|
|
1 |
|
|
|
|
|
= e . |
|||
x |
= e , lim (1+ x)x |
|||||
|
|
|
x→0 |
|
||
|
Пример 5. lim |
tgx |
= |
|
0 |
= lim |
sin x |
lim |
1 |
=1 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
x |
|
|
x |
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
x→0 |
|
|
|
0 |
x→0 |
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
||||
|
Пример 6. |
|
|
1−2x |
x |
= lim |
(1+ x) − x −2x x |
= lim |
|
|
+ |
|
−3x x |
= |
∞ |
} |
= |
|||||||||||||||||
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
+ x |
|
|
|
|
1+ x |
|
|
|
|
|
|
{ |
|
|||||||||||||
|
|
|
|
|
|
x→0 |
|
x→0 |
|
|
|
x→0 |
|
|
|
1+ x |
|
|
|
|
||||||||||||||
|
|
|
|
1+x |
|
−3x 2 |
|
|
|
|
−6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
−3x −3x 1+x x |
|
|
lim→ |
|
|
|
|
= e−6 = |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= lim 1+ |
|
|
|
|
= ex |
0 1+x |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
e |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x→0 |
|
1+ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

60
При сравнении бесконечно малых функций используют определенную терминологию. Определение 3. Пусть f (x) и g(x) – бесконечно малые функции при x → x0 .
Говорят, что эти функции одного порядка малости при x → x0 , если
lim f (x) = C ≠ 0 .
x→x0 g(x)
Если же
lim f (x) = 0 ,
x→x0 g(x)
то f (x) есть бесконечно малая более высокого порядка при x → x0 .
Например, судя по первому замечательному пределу, функции sin x и x одного
порядка малости. |
|
|
|
|
Определение 4. Функции f (x) |
и g(x) называются эквивалентными при x → x0 , если |
|||
|
lim |
f (x) |
|
=1. |
|
g(x) |
|||
|
x→x0 |
|
||
Символически это записывается так: |
f (x) g(x) , |
x → x0 . |
||
У эквивалентных функций есть замечательное свойство. Их можно заменять друг на друга под знаком предела.
Имеет место следующая эквивалентность бесконечно малых:
x sin x tgx arcsin x arctgx ln(1+ x) ex −1, x → 0 .
|
x2actg3x |
0 |
|
|
3x3 |
|
3 |
|
||
Пример 7. lim |
|
= |
|
|
= lim |
|
= |
|
. |
|
ln(1+ 4x3 ) |
0 |
4x3 |
4 |
|||||||
x→0 |
|
|
x→0 |
|
|
|||||
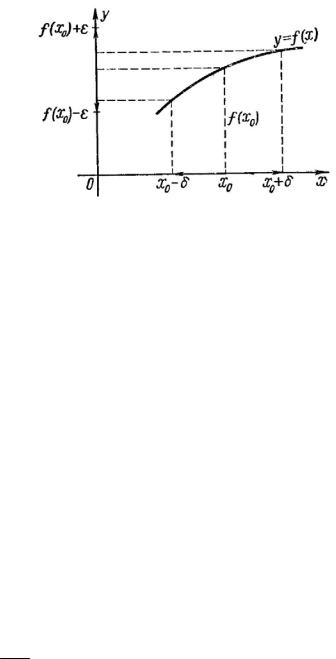
61
Лекция 4. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
План
1.Точки непрерывности и точки разрыва функции.
2.Непрерывность элементарных функций. Свойства непрерывных функций.
1. Важнейшим понятием математического анализа является непрерывность функции. Определение 1. Функция f (x), определенная в некоторой окрестности точки x0 ,
называется непрерывной в этой точке, если предел функции в точке x0 существует и равен значению в этой точке:
lim f (x)= f (x0 ).
x→x0
Рис. 1. Иллюстрация непрерывности функции в точке x0
|
Определение 1 содержит четыре условия непрерывности: |
|
1) |
функция f (x) должна быть определена в некоторой окрестности точки x0 ; |
|
2) |
должны существовать конечные односторонние пределы lim f (x) и |
lim f (x); |
|
x→x0 −0 |
x→x0 +0 |
3) |
эти пределы должны быть одинаковы; |
|
4) |
эти пределы должны быть равны f (x0 ). |
|
Определение 2. Если в точке x0 нарушается хотя бы одно из условий непрерывности, то говорят, что эта точка есть точка разрыва функции f (x). Причем, если выполняется
условие 2) и не выполняется хотя бы одно из оставшихся, то это точка разрыва первого рода. Если же условие 2) не выполняется, то это точка разрыва второго рода.
Например, функция y = |
|
|
x |
|
|
(рис. 2, а) терпит разрыв первого рода в точке x = 0 , т.к. |
|
|
x |
|
|
||
|
|
|||||
|
|
|
|
|
|
односторонние пределы существуют, но они не равны:
lim |
x |
= −1; |
lim |
x |
=1 . |
|
x |
x |
|||||
x→0−0 |
|
x→0+0 |
|
Заметим, что разность между конечными значениями правостороннего и левостороннего пределов называют скачком функции в точке. В данном случае величина скачка равна 2.
Функция y = x1−1 (рис. 2, б) имеет разрыв второго рода в точке x =1 , т.к. в этой точке не существуют конечные односторонние пределы:

62
lim |
1 |
|
= −∞; lim |
1 |
|
= +∞. |
|
x −1 |
x −1 |
||||||
x→1−0 |
x→1+0 |
|
|||||
|
а |
|
|
б |
|
|
Рис. 2. Иллюстрация точек разрыва а) первого рода и б) второго рода |
||||
2. |
Элементарные |
функции: |
степенные, |
показательные, |
логарифмические, |
тригонометрические и обратные им, а также их сумма, произведение, частное непрерывны при всяком x , при котором они имеют определенное значение.
Обратим внимание на свойства непрерывных функций. |
|
|
|
Теорема 1. Если функции f (x) и g(x) непрерывны в точке |
x0 , то функции Cf (x) |
||
( C = const ), f (x) + g(x) , f (x) g(x) , а если, кроме того, g(x ) ≠ 0 , |
то и |
f (x) |
, являются |
|
|||
0 |
|
g(x) |
|
|
|
||
непрерывными в точке x0 .
Теорема 2. Непрерывная функция от непрерывной функции является непрерывной функцией.
Определение 3. Функция, определенная на некотором отрезке и непрерывная в каждой его точке, называется непрерывной на отрезке.
Теорема 3 (Вейерштрасс). Всякая непрерывная на отрезке функция ограничена. Теорема 4 (Вейерштрасс). Всякая непрерывная на отрезке функция имеет на этом
отрезке как наибольшее, так и наименьшее значение.
Теорема 5 (Коши). Непрерывная на отрезке функция, принимающая какие-либо два значения, принимает и любое промежуточное.
Следствие из теоремы Коши. Если функция непрерывна на отрезке и на его концах принимает значения разного знака, то на этом отрезке существует точка, в которой функция обращается в ноль.
Заметим, что последний факт полезен при нахождении корней уравнений точно или приближенно.
63
I I I.б ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Лекция 1. ПРОИЗВОДНАЯ ФУНКЦИИ В ТОЧКЕ
План
1.Определение производной и ее физический смысл.
2.Геометрический смысл производной. Уравнение касательной к графику функции.
3.Правила дифференцирования. Производная обратной и сложной функций.
1. Пусть функция y = f (x) определена в некоторой окрестности точки x0 . Для любой точки x из этой окрестности приращение аргумента [приріст, increase] ∆x определяется формулой
∆x = x − x0 , откуда x = x0 +∆x . Приращением |
функции y = f (x) в |
точке x0 |
называется |
||||
разность |
|
|
|
|
|
|
|
∆y = f (x)− f (x0 )= f (x0 +∆x)− f (x0 ). |
y = f (x) |
|
|||||
Определение 1. Производной [похідною, derivative] от функции |
в точке x0 |
||||||
называется предел отношения ∆y |
, когда ∆x → 0 : |
|
|
|
|||
∆x |
|
|
f (x0 |
+∆x)− f (x0 ) |
|
|
|
f ′(x0 )= lim |
∆y |
= lim |
, |
|
(1) |
||
∆x |
|
∆x |
|
||||
∆x→0 |
∆x→0 |
|
|
|
|
||
при условии, что этот предел существует. В этом случае говорят, что функция y = f (x) дифференцируема [диференційовна, differentiable] в точке x0 , а саму процедуру вычисления
производной называют дифференцированием [диференціювання, derivation] функции в этой точке.
Заметим, что предел (1) может не существовать. В этом случае говорят, что функция f (x) не имеет производной (не дифференцируема) в точке x0 . Если предел (1) равен +∞
или −∞, то говорят, что функция |
|
f (x) имеет в точке x0 бесконечную производную, равную |
|||||||||||||
+∞ или −∞, соответственно. |
y = f (x) в точке |
x0 обозначают y′(x0 ) или |
f ′(x0 ). |
|
|
||||||||||
Производную функции |
Если |
||||||||||||||
необходимо указать, какая переменная является независимой (в данном |
случае |
x – |
|||||||||||||
независимая переменная), то используются обозначения: |
|
|
|
||||||||||||
|
|
|
|
|
yx′, |
dy , |
dy |
|
. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
dx |
dx |
|
x=x |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
d |
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Например, выражение |
|
x + |
|
|
следует понимать как производную функции y = x + |
x |
|||||||||
|
|||||||||||||||
|
dx |
x |
|
x=2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
по переменной x в точке x0 = 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 1. Рассмотрим функцию f (x)= C |
(const). Для любой точки x0 |
приращение |
|||||||||||||
∆y = 0 . Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C′ = lim |
∆y |
= 0 . |
|
|
|
|
||||
|
|
|
|
|
|
∆x→0 |
∆x |
|
|
|
|
|
|
|
|
Пример 2. Пусть |
f (x)= x . Для любой точки x0 |
приращение ∆y = ∆x . Поэтому |
|
|
|||||||||||
|
|
|
|
|
x′ = lim |
∆y = lim |
∆x |
=1. |
|
|
|
||||
|
|
|
|
|
∆x→0 |
∆x |
∆x→0 |
∆x |
|
|
|
|
|||

64
Физический смысл производной следующий. В самых различных задачах (в том числе и экономических) производная функции y = f (x) интерпретируется как скорость изменения
величины y относительно x .
2. Геометрический смысл производной состоит в том, что f ′(x0 ) – это тангенс угла наклона касательной к графику функции y = f (x) в точке (x0 , f (x0 )).
Обозначим через Γ |
график |
функции y = f (x). Найдем уравнение касательной к |
|||
графику |
Γ |
в точке |
A(x0 , |
f (x0 )). Будем искать это уравнение в виде y = kx +b . Так как |
|
A Γ, |
то |
должно |
выполняться |
равенство f (x0 )= kx0 +b , откуда b = f (x0 )−kx0 . |
|
Следовательно касательная задается уравнением
y = kx + f (x0 )−kx0 = k (x − x0 )+ f (x0 ).
Поскольку угловой |
коэффициент касательной |
k = f ′(x0 ), то уравнение |
касательной |
[рівняння дотичної, tangent equation] имеет вид |
|
|
|
|
y = f ′(x0 )(x − x0 )+ f (x0 ). |
(2) |
|
Определение |
2. Пусть функция y = f (x) |
непрерывна на отрезке |
[a,b] . Будем |
называть функцию гладкой [гладка, smooth] на отрезке [a,b] , если в каждой точке этого
отрезка можно провести единственную касательную к графику функции. Точки непрерывности функции, в которых можно провести не единственную касательную,
называют угловыми точками или точками излома графика.
Т.о. для наличия дифференцируемости одной непрерывности функции не достаточно. Должна иметь место и гладкость [гладкість, smoothness] функции.
Утверждение 1. Для того, чтобы функция y = f (x) была дифференцируема в точке x0 необходимо и достаточно, чтобы в этой точке она была гладкой.
Пример 3. Функция y = x имеет область определения D( y) = R . Эта функция
непрерывна во всех точках области определения. Функция является гладкой на всей области определения, кроме точки x0 = 0 . Точка x0 = 0 является угловой и касательных в ней можно
провести бесконечное множество (рис. 1). Согласно утверждению 1, функция y = x в точке x0 = 0 не является дифференцируемой.
Пример 4. Найти уравнение касательной к графику функции y = x2 в точке (1;1). Решение. Т.к.
(x2 )′x=1 = (2x)x=1 = 2 ,
то согласно (2) уравнение касательной будет таким
y = 2(x −1)+1 = 2x −1.

65
Рис. 1. Иллюстрация к примеру 3
3. Перечислим правила дифференцирования, которые сводят вычисление производных одних функций к вычислению производных других (более простых) функций.
Утверждение 2. (правила дифференцирования). Если функции u = f (x), v = g (x) дифференцируемы в точке x0 , то сумма, разность, произведение и частное этих функций (частное при условии g (x0 )≠ 0 ) также дифференцируемы в точке x0 , и имеют место следующие формулы:
(u ±v)′ = u′±v′,
|
′ |
|
′ |
|
|
′ |
|
(uv) |
= u v +uv |
|
, |
||||
|
′ |
|
′ |
|
|
′ |
|
u |
= |
u v −uv |
|
. |
|||
|
|
|
v |
2 |
|
||
v |
|
|
|
|
|
||
Пример 5. Пусть C – const. |
Т.к. |
x′ =1 |
и C′ = 0 , то по первому правилу |
||||
дифференцирования
(x +C )′ =1 .
Второе правило дифференцирования позволяет доказать важное следствие. Следствие. При дифференцировании константу C можно выносить за знак
производной:
(Cf (x))′ = Cf ′(x) .
Доказательство. По второму правилу дифференцирования имеем
′ |
′ |
|
|
′ |
|
|
|
|
′ |
′ |
(Cf (x)) = C |
|
f (x) +Cf (x) = |
|
0 f (x) +Cf (x) = Cf (x) . |
||||||
Пример 6. Найдем производную функции |
|
y = |
1 x2 |
: |
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
y′ = 1 x2 |
′ |
= 1 |
(x x)′ = 1 |
(x′x + xx′)= |
1 |
2x = x . |
||||
2 |
|
2 |
2 |
|
|
|
|
2 |
|
|
Пример 7. Продифференцируем функцию |
y = |
1 : |
|
|
|
|||||
|
|
|
|
|
|
|
x |
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
66 |
|
|
|
|
|
|
1 |
|
′ |
|
|
|
′ |
x |
|
−1 x |
′ |
|
0 x −1 1 |
|
|
|
1 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
y′ |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
= |
= |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
= |
|
|
2 |
|
|
|
= − |
|
|
. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
x |
2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функция y = f (x) |
|
||||||||
Утверждение 3 (производная обратной функции). Если |
имеет |
|||||||||||||||||||||||||||||||||||||||
обратную функцию x = g (y) |
и в точке |
|
x0 |
|
производная |
|
f ′(x0 )≠ 0 , |
то обратная функция |
||||||||||||||||||||||||||||||||
g (y) дифференцируема в точке y0 = f (x0 ) и имеет место формула |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
g′(y0 )= |
|
|
|
|
1 |
|
|
|
, или x′y = |
|
1 |
. |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
f |
′(x0 ) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yx′ |
|
|
|
|
|
функция y = f (x) |
|||||||||||
Утверждение 4 (производная сложной |
функции). Если |
|||||||||||||||||||||||||||||||||||||||
дифференцируема в |
точке |
t0 |
и |
g(t0 ) = x0 , |
|
то |
сложная |
функция y = f (g(t)) |
также |
|||||||||||||||||||||||||||||||
дифференцируема в t0 |
и имеет место формула |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
f (g(t)) |
|
|
= |
|
|
f ′(x0 ) g′(t0 ), или yt′ = yx′ xt′. |
|
|
|
|
||||||||||||||||||||||||||
|
|
dt |
t=t0 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 +1 . |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Пример 8. Найти производную функции y = |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Решение. Опираясь на утверждение 4, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
2 |
|
′ |
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
′ |
|
1 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|||||
y′ = ( x |
|
|
+1) = |
|
|
|
|
|
|
|
|
|
|
(x |
|
+1) |
= |
|
|
|
|
|
|
|
2x = |
|
|
|
. |
|
||||||||||
|
|
2 |
x |
2 |
|
+1 |
|
2 |
x |
2 |
+1 |
x |
2 |
+1 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||

67
Лекция 2. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
План
1.Производные элементарных функций.
2.Дифференциал.
3.Приближенные вычисления с помощью дифференциала.
1. Поместим в табл. 1 производные элементарных функций. При наличии аргумента u = u(x) речь идет о сложной функции.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Табл. 1. Производные элементарных функций |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Функция y = f (x) |
|
Производная y′ |
|
Функция y = f (u) |
|
|
|
Производная y′ |
|||||||||||||||||||||||||||||||||||||||||||
y = xα |
|
|
y′ =αxα−1 |
|
|
|
|
y = uα |
|
|
|
|
y′ =αuα−1 u′ |
|
|||||||||||||||||||||||||||||||||||||
y = ax |
|
y′ = ax ln a |
|
|
|
|
y = au |
|
|
|
|
y′ = au ln a u′ |
|
||||||||||||||||||||||||||||||||||||||
y = ex |
|
|
|
|
|
|
y′ = ex |
|
|
|
|
y = eu |
|
|
|
|
|
y′ = eu u′ |
|
||||||||||||||||||||||||||||||||
y = loga x |
|
|
y′ = |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
y = loga u |
|
|
|
|
|
y′ = |
|
u′ |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
x ln a |
|
|
|
|
|
|
|
|
|
u ln a |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
y = ln x |
|
|
|
|
|
|
y′ = |
1 |
|
|
|
|
|
|
|
|
|
|
y = ln u |
|
|
|
|
|
|
|
|
|
y′ = u′ |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|||||||
y = sin x |
|
|
y′ = cos x |
|
|
|
|
y = sin u |
|
|
|
|
y′ = cosu u′ |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
y = cos x |
|
y′ = −sin x |
|
|
|
|
y = cosu |
|
|
|
|
y′ = −sin u u′ |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = tgx |
|
y |
′ |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
y = tgu |
|
|
|
|
y |
′ |
|
|
|
|
|
|
u′ |
|
|
|
|
|
|
|
|||||||
|
|
= cos2 x |
|
|
|
|
|
|
|
|
|
= cos2 u |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
y = ctgx |
|
y |
′ |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
y = ctgu |
|
|
|
|
y |
′ |
|
|
|
|
|
|
|
|
u′ |
|
|
||||||||
|
|
|
= −sin2 x |
|
|
|
|
|
|
|
|
|
|
= −sin2 u |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
y = arcsin x |
|
y′ = |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
y = arcsin u |
|
|
|
|
y′ |
|
|
= |
|
|
|
|
u |
′ |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1− x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1−u2 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
y = arccos x |
|
y′ = − |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
y = arccosu |
|
|
|
y′ = − |
|
|
u |
′ |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
1− x2 |
|
|
|
|
|
|
|
|
1−u2 |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
y = arctgx |
|
y |
′ |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
y = arctgu |
|
|
|
|
y |
′ |
|
|
|
|
|
u′ |
|
|
|
|
|
|
|
|||||||||
|
= x2 +1 |
|
|
|
|
|
|
|
|
= u2 +1 |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
y = arcctgx |
|
y |
′ |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
y = arcctgu |
|
|
|
|
y |
′ |
|
|
|
|
|
|
|
u′ |
|
|
||||||||||
|
|
= − x2 +1 |
|
|
|
|
|
|
|
|
|
= −u2 +1 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Пример 1. Найти производную функции y = log2 (1+sin4 x). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Решение. Воспользовавшись табл. 1, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
1+sin |
4 |
|
|
x |
′ |
|
3 |
|
|
′ |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
) |
|
|
|
|
|
|
4sin |
|
x (sin x) |
|
4sin x cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
y′ = |
( |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
1+sin4 x |
) |
ln 2 |
|
1+sin4 x |
) |
ln 2 |
1+sin4 x |
) |
ln 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. Введем понятие дифференциала.
68
Определение 1. Дифференциалом функции [диференціалом функції, differential of
function] y = f (x) в точке x0 называется линейная функция |
относительно приращения |
аргумента ∆x : |
|
dy = f ′(x0 )∆x . |
(1) |
Дифференциал функции y = f (x) обозначается dy или df (x0 ). Главное назначение дифференциала состоит в том, чтобы заменить приращение ∆y на линейную функцию от
∆x , совершив при этом, по возможности, меньшую ошибку. Имеет место следующее утверждение.
Утверждение. Если функция y = f (x) имеет в точке x0 конечную производную f ′(x0 ), то приращение функции ∆y представимо в виде
∆y = f ′(x0 )∆x +α(∆x)∆x , |
(2) |
где функция α(∆x)→ 0 при ∆x → 0 .
При выполнении свойства (2) функцию называют дифференцируемой в точке x0 , что
равносильно наличию в этой точке конечной производной. Действительно, из (2) следует, что
lim |
∆y |
= lim |
f ′(x0 )∆x +α(∆x)∆x |
= lim |
(f ′(x0 )+α(∆x))= f ′(x0 )+0 = f ′(x0 ). |
|
∆x |
∆x |
|||||
∆x→0 |
∆x→0 |
∆x→0 |
|
Используя (1), запишем формулу (2) в виде
∆y = dy +α(∆x)∆x .
Если приращение аргумента ∆x будет достаточно малым, то последнее равенство можно заменить приближенным
∆y ≈ dy , |
(3) |
которое часто используют в приближенных вычислениях. Замечание. Пусть f (x) = x . Т.к. x′ =1, то, согласно (1), имеем
dx = ∆x .
Поэтому (1) можно записывать в виде
dy = f ′(x0 )dx ,
а саму производную обозначать как dydx .
3. Поговорим теперь о том, как понятие дифференциала используется в приближенных вычислениях.
Пример 2. Пусть r – радиус круга, S =π r2 – его площадь. Используя (3), получим
∆S ≈ dS = 2πr∆r ,
т.е. приращение площади круга приближенно равняется произведению длины его окружности на приращение радиуса.
В силу того, что по определению
∆y = f (x0 +∆x)− f (x0 ),
то формула (3) может быть записана в виде
f (x0 + ∆x)≈ f (x0 )+ f ′(x0 )∆x . |
(4) |
|||||||
Если x0 = 0 , то ∆x = x и равенство (4) будет следующим |
|
|
|
|
|
|
||
f (x)≈ f (0)+ f ′(0)x . |
(5) |
|||||||
Используя формулу (5), следует помнить, что величина |
|
x |
|
(так же как и |
|
∆x |
|
в (3), (4)) |
|
|
|
|
|||||
должна быть достаточно малой. |
|
|
|
|
|
|
||

69
|
|
′ |
|
1 |
|
|
|
Пример 3. Пусть f (x)= |
1+ x . Т.к. f |
(0)= 2 |
, то при достаточно малых x |
имеем |
|||
|
|||||||
|
1+ x ≈1+ |
1 x . |
|
||||
|
|
|
|
2 |
|
|
|
В качестве достаточной малости будем понимать, что x <<1 .
Найдем приближенное значение 0,99 . Используя последнее равенство, получим
0,99 = 1−0,01 ≈1− 12 0,01 = 0,995 .
Калькулятор дает следующий результат: 0,99 ≈ 0,99498744 .
Пример 4. Докажите самостоятельно, что при x <<1 имеют место следующие
приближенные равенства:
(1+ x)α ≈1+αx ,
ex ≈1+ x , ln (1+ x)≈ x ,
sin x ≈ x .
Пример 5. Пусть r – годовая процентная банковская ставка, S(0) – начальная сумма
на счете. Если для начисления используется схема сложных процентов, то через время T (будем измерять его в годах) на счете будет сумма
S(T ) = S(0)(1+r )T .
Найдем количество лет T , в течение которых начальная сумма вклада S(0) увеличится в два раза. Для этого нужно решить относительно T уравнение
2S(0) = S(0)(1+ r )T .
Логарифмируя это уравнение, получим
|
|
|
|
|
|
|
T ln (1+r )= ln 2 . |
|
|
|
||
Откуда T = |
|
|
ln 2 |
|
|
|
||||||
|
|
|
|
|
. |
|
|
|
|
|
||
ln (1+r ) |
|
|
|
|||||||||
|
Если |
|
r |
|
<<1, то используя приближенное равенство из примера 4, найдем |
|||||||
|
|
|
||||||||||
|
|
|
|
|
|
|
T ≈ |
ln 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
r |
|
0,7 |
|
|
Т.к. |
ln 2 ≈ 0,7 , то время удвоения вклада приближенно равно |
T ≈ |
. Если, например, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
r |
|
ставка процента r =10% = 0,1, то время удвоения вклада составит приблизительно 7 лет.
70
Лекция 3. ПРОИЗВОДНАЯ И ЭКОНОМИЧЕСКИЕ ЗАДАЧИ
План
1.Предельные величины в экономике.
2.Эластичность и ее свойства.
3.Ценовая эластичность спроса.
4.Распределение налогового бремени.
1. Теоретический анализ разнообразных явлений экономики использует ряд предельных величин. Перечислим лишь некоторые: предельные издержки [граничні витрати, marginal cost, input], предельный доход [доход, income, profit], предельная производительность [продуктивність, productivity], предельная полезность [корисність, utility], предельная склонность к потреблению [схильність до споживання, disposition to consumption] и т.д. Все эти величины самым тесным образом связаны с понятием производной. В качестве характерного примера рассмотрим предельные издержки.
Пусть q – количество [кількість, quantity] произведенной продукции, C (q) –
соответствующие данному выпуску издержки производства. Предельные издержки [граничні витрати, marginal cost] обозначаются MC и определяются как дополнительные издержки, связанные с производством еще одной единицы продукции. Другими словами,
MC = C (q +∆q)−C (q),
где ∆q =1. Используя равенство ∆C ≈ dC , получим
MC = ∆C ≈ dC = C′(q) ∆q = C′(q).
Т.о., данное выше определение MC , по существу, не противоречит другому распространенному определению, согласно которому MC = C′(q).
Пример 1. Пусть издержки производства q единиц продукции подчиняются следующему соотношению C (q)=1500q −2q2 +0,002q3 грн. Тогда дополнительные издержки, связанные с увеличением выпуска от q до q +1 (т.е. предельные издержки), составят ∆C = C (q +1)−C (q), что приближенно равно
C′(q)=1500 −4q +0,006q2 .
В табл. 1 приведены значения ∆C и C′(q), которые, как видно, мало отличаются друг от друга.
|
|
Табл. 1. Расчетные данные к примеру 1 |
|
|
|
|
|
q |
C′ |
∆C |
|
100 |
1160 |
1158,6 |
|
200 |
940 |
939,2 |
|
300 |
840 |
839,8 |
|
400 |
860 |
860,4 |
|
500 |
1000 |
1001,0 |
|
600 |
1260 |
1261,6 |
|
700 |
1640 |
1642,2 |
|
800 |
2140 |
2142,8 |
|
900 |
2760 |
2763,4 |
|
1000 |
3500 |
3504,0 |
|

71
Общая схема введения предельных величин такова: пусть величина Y является функцией от величины X , тогда предельная величина MY (по X ) определяется как
отношение ∆∆XY . Приращение ∆X в различных случаях задается по-разному. В одних
случаях ∆X – это наиболее естественная единица измерения величины X , в других случаях ∆X – это разность между соседними значениями X в таблице, задающей функцию Y и X . В теоретических вопросах, однако, более удобным является определение MY , основанное на равенстве
MY =Yx′.
Конечно, при таком определении приходится дополнительно предполагать, чтоY является дифференцируемой функцией от X .
2. Понятие эластичности [еластичності, elasticity] было введено Аланом Маршаллом в связи с анализом функции спроса [попиту, demand]. По существу, это понятие является чисто математическим и может применяться при анализе любых дифференцируемых функций.
Определение 1. Эластичностью функции y = f (x) |
в точке x0 называется следующий |
||||||
предел |
|
|
|
|
|
|
|
Eyx |
(x0 ) = lim |
|
∆y |
: |
∆x |
|
(1) |
|
. |
||||||
|
∆x→0 |
|
y |
|
x |
|
|
Говорят также, что Eyx (x0 ) – это коэффициент эластичности y по x .
Если из контекста ясно, в какой точке определяется эластичность и какая переменная является независимой, то в обозначении эластичности могут опускаться отдельные символы. Мы тоже будем использовать сокращенные обозначения Ey и Eyx .
Из определения эластичности вытекает, что при достаточно малых ∆x выполняется приближенное равенство
|
∆y |
: ∆x |
≈ Ey , |
|
|
y |
x |
|
|
которое можно записать в виде |
|
|
|
|
∆y |
≈ Ey |
∆x |
|
|
y |
x . |
|
(2) |
|
Из (2) следует смысл эластичности. Эластичность Ey |
– это коэффициент |
|||
пропорциональности между относительными изменениями величин y и x . Если, например, x увеличится на один процент, то y увеличивается (приближенно) на Ey процентов.
Ниже нам потребуется несколько формул, выражающих эластичность через производные функции. Из (1) заметим, во-первых, что
Eyx (x0 ) = lim |
|
f (x0 + ∆x) − f (x0 ) |
|
|
|
∆x |
|
|
|
x0 |
|
|
f (x0 +∆x) − f (x0 ) |
|
|
x0 |
|
f ′(x0 ) |
|||||||
|
: |
|
|
|
|
= |
|
|
lim |
= |
|
|
|||||||||||||
|
|
x |
+ ∆x |
|
f (x |
|
|
|
f (x |
) |
|||||||||||||||
|
|
|
∆x→0 |
|
|
f (x ) |
|
) ∆x→0 |
∆x |
|
|||||||||||||||
или |
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Ey |
= |
y′. |
|
|
|
|
|
|
|
|
(3) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
||
|
Т.о., если x0 |
≠ 0 и |
f (x0 ) ≠ 0 , то для существования конечного предела (1) в точке x0 |
||||||||||||||||||||||
необходимо и достаточно, чтобы существовала конечная производная f ′(x0 ) . |
|
|
|
||||||||||||||||||||||
|
Во-вторых, |
|
если |
использовать |
|
понятие |
|
логарифмической производной, т.е. |
|||||||||||||||||
′ |
|
y′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ln y) |
= |
|
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Ey |
= x(ln y)′. |
|
|
|
|
|
|
|
|
(4) |
||||||||

|
|
|
|
|
|
|
72 |
|
Наконец, в-третьих, заметим, что x = |
|
1 |
|
= |
1 |
, поэтому эластичность Ey |
совпадает с |
|
|
1 |
(ln x)′ |
||||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x |
|
|
|
|
|||
отношением логарифмических производных |
|
|
|
|||||
Ey = |
(ln y)′ . |
|
(5) |
|||||
|
|
(ln x)′ |
|
|||||
Пример 2. Пусть издержки производства q ед. продукции подчиняются следующему |
||||||||
соотношению C (q)=1500q −2q2 +0,002q3 |
грн. |
(см. пример 1). Найти |
показатель |
|||||
эластичности при q0 =100 ед. и объяснить его численное значение.
Решение. Воспользуемся формулой (3), записав ее в соответствующих обозначениях:
EC (q) = Cq C′.
Нами записана формула эластичности издержек производства C по количеству
произведенной продукции q . Формула содержит предельные издержки C′, найденные в примере 1. В итоге, получим
|
|
E (q) = |
q(1500 −4q +0,006q2 ) |
= 1500 |
−4q +0,006q2 . |
|
|||||||
|
|
C |
|
1500q −2q2 +0,002q3 |
1500 |
−2q +0,002q2 |
|
||||||
При q0 =100 имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
(100) = |
1500 −4 |
100 |
+0,006 |
10000 = 1500 |
−400 |
+60 |
= 1160 |
= 29 |
≈ 0,88 . |
|||
C |
|
1500 |
−2 |
100 |
+0,002 |
10000 1500 |
−200 |
+ 20 |
1320 |
33 |
|
||
|
|
|
|||||||||||
Т.о., при выпуске 100 ед. продукции, если количество выпускаемой продукции увеличится на 1%, т.е. на 1 ед., то издержки производства увеличатся на 0,88%, т.е. на
|
0,88% C (100)= 0,0088(1500 100 −2 10000 +0,002 1000000)=1161,6 (грн.) |
||||||
|
100% |
|
|
|
|
|
|
Рассмотрим теперь свойства эластичности. |
|
|
|
|
|||
1. |
Эластичность является безразмерной величиной и не зависит от выбора единиц |
||||||
измерения величин y и x (см. (1)). |
|
|
|
|
|
||
2. |
Эластичность в точке x0 суммы y = y1 +... + yn положительных функций yi = fi (x) |
||||||
(i =1,2,...,n) удовлетворяет соотношению |
|
|
|
|
|
||
|
|
Emin ≤ Ey ≤ Emax , |
|
|
|
(6) |
|
где Emin |
( Emax ) – это минимальная (максимальная) эластичность в точке x0 |
функций yi . |
|||||
3. |
Эластичность произведения функций u =u(x) и v = v(x) |
в точке x0 |
равна сумме |
||||
эластичностей функций u и v в той же точке: |
|
|
|
(7) |
|||
|
|
Euv = Eu + Ev . |
|
|
|
||
4. |
Эластичность частного функций |
u = u(x) и v = v(x) в точке x0 |
(v(x0 ) ≠ 0) равна |
||||
разности эластичностей функций u и v в той же точке: |
|
|
|
(8) |
|||
|
|
Eu / v = Eu |
− Ev . |
|
|
|
|
5. |
Для функций |
y = f (x) и x = g(t) |
эластичность y |
по t |
в точке t0 удовлетворяет |
||
следующему равенству: |
Eyt (t0 ) = Eyx (g(t0 ))Ext (t0 ) . |
|
|
|
(9) |
||
|
|
|
|
|
|||
6. |
Для функции |
y = f (x) эластичность обратной |
функции x = g( y) |
в точке y0 |
|||
удовлетворяет соотношению: |
|
|
|
|
(10) |
||
|
|
Exy ( y0 ) = Eyx−1 (g( y0 )) . |
|
|
|
||
Пример 3. Пусть y = C – const. Используя (3), получим |
|
|
|
||||

73
EC = x CC′ = 0 .
Пример 4. Найти эластичность функции y = x +C , C – const.
Решение. По формуле (3) получаем
Ey = x (xx++CC)′ = x +xC .
Пример 5. Найти эластичность степенной функции y = xa . Решение. Применяя формулу (4), находим эластичность
Ey = x(ln xa )′ = x(a ln x)′ = x a 1x = a .
3. Скажем теперь несколько слов о ценовой эластичности спроса.
Пусть D = D( p) – спрос [попит, demand] (в натуральных единицах) на некоторый товар при цене p . Так как при увеличении цены спрос уменьшается, то эластичность спроса
ED < 0 .
Определение 2. Спрос называется эластичным [еластичним, elastic], если ED >1 (т.е. процент изменения величины спроса больше процента изменения цены товара), и
неэластичным, если ED <1. Термин совершенно неэластичный спрос означает крайний
случай, когда изменение цены не приводит ни к какому изменению спроса. В этом случае ED = 0 . В другом крайнем случае, когда самое малое снижение цены побуждает покупателя
увеличивать покупки от нуля до предела своих возможностей, говорят, что спрос является совершенно эластичным. Можно считать, что для совершенно эластичного спроса ED =∞.
Если спрос со стороны отдельных покупателей или групп покупателей является эластичным (неэластичным), то и суммарный спрос также является эластичным (неэластичным).
Если продавцы обладают достаточными запасами товара, то покупатели могут полностью реализовывать свои потребности. Поэтому D = D( p) – это не только количество
спрашиваемого товара, но и одновременно количество проданного товара. В данном случае общая выручка (доход) [виручка, виторг, доход, revenue, proceeds, income] всех продавцов R = pD . Найдем эластичность выручки по цене
|
R |
′ |
′ |
′ |
|
D + pD |
′ |
|
D |
′ |
|
|
|
p |
|
|
|
|
|||||||
ER = |
|
p = |
p D + pD |
|
= |
|
=1+ |
|
p =1+ ED . |
|||
|
|
pD |
|
pD |
|
D |
||||||
|
R |
|
|
|
|
|
||||||
Следовательно, при эластичном спросе ER < 0 , а при неэластичном спросе ER > 0 .
Вывод: Если спрос эластичен, то изменение цены вызывает изменение общей выручки в противоположном направлении. Если же спрос неэластичен, то изменение общей выручки происходит в том же направлении, что и изменение цены.
4. Одной из экономических задач, в которой используется понятие производной, является
задача о распределении налогового бремени.
Пусть p – цена товара на некотором рынке, S( p) – его предложение [пропозиція, supply] при цене p , D( p) – спрос. Равновесная цена p0 определяется уравнением
S( p0 ) = D( p0 ) .
Предположим, что вводится дополнительный налог [податок, tax] с производителей в размере t с каждой единицы товара. Т.к. зависимость предложения от цены определяется прибылью, а при цене p и налоге t прибыль такая же, что и при цене p −t и отсутствии
дополнительного налога, то St ( p) = S( p −t) , где St ( p) – функция предложения после

74
введения налога. Т.о., кривая предложения после введения налога сдвигается на t вверх (рис. 1).
Рис. 1. Кривые спроса и предложения
Пусть pt – новая равновесная цена. Равенство спроса и предложения при цене pt
выражается уравнением |
St ( pt ) = D( pt ) , |
|
||
которое равносильно уравнению |
|
|||
|
|
(11) |
||
S( pt |
−t) = D( pt ) . |
|||
Заменяя приращения функций S( p) |
и D( p) в точке p0 на их дифференциалы, согласно (4), |
|||
получим (приближенные) равенства: |
|
|
(12) |
|
S( p0 +∆p) = S( p0 ) + S′( p0 )∆p , |
||||
D( p0 +∆p) = D( p0 ) + D′( p0 )∆p , |
(13) |
|||
в которых ∆p = p1 − p0 – изменение равновесной цены. С учетом |
(12.15), (13.15) равенство |
|||
(11) приобретает вид |
|
|
|
|
S( p0 ) + S′( p0 )(∆p −t) = D( p0 ) + D′( p0 )∆p . |
|
|||
Т.к. S( p0 ) = D( p0 ) , то последнее равенство равносильно равенству |
|
|||
S′( p0 )(∆p −t) = D′( p0 )∆p . |
|
|||
Откуда |
tS′( p0 ) |
|
||
∆p = |
|
|
||
|
. |
(14) |
||
S′( p0 ) − D′( p0 ) |
||||
Итак, после введения дополнительного налога на покупку единицы товара затраты потребителя увеличатся на величину ∆p , которую можно (приближенно) рассчитать по
формуле (14). Соответственно, доход производителя (также на единицу продукции) уменьшится на
t −∆p = |
−tD′( p0 ) |
|
|
. |
|
S′( p0 ) − D′( p0 ) |
||
Из (14) и последнего равенства следует, налоговое бремя распределяется между потребителями и производителями продукции в отношении
∆p :[t −∆p]= S′( p0 ) :[−D′( p0 )].
Поскольку в точке p0 спрос равен предложению, то

75
S′( p0 ) :[−D′( p0 )]= S′( p0 ) p0 : −D′( p0 ) p0 = ES :[−ED ],
S( p0 ) D( p0 )
где ED , ES – коэффициенты эластичности спроса и предложения в точке p0 . Полученное соотношение позволяет записать (14) в следующем виде:
∆p = 1− D1′( p0 )
S′( p0 )
t = |
|
1 |
t = |
ES |
t . |
(15) |
|
|
|
ED |
ES − ED |
||||
1− |
|
ES |
|
|
|
|
|
Пример 6. Пусть ценовая эластичность спроса ED = −3, ценовая эластичность предложения ES = 2 , а вводимый налог t =100 . Согласно (15), цена после введения этого
налога увеличится на величину
∆p = 2 +2 3 100 = 40 ,
а прибыль производителя от единицы продукции уменьшится на t −∆p =100 −40 = 60 .

76
Лекция 4. ТЕОРЕМЫ, СВЯЗАННЫЕ С ПОНЯТИЕМ ПРОИЗВОДНОЙ
План
1.Теоремы о промежуточных значениях.
2.Раскрытие основных неопределенностей по правилам Лопиталя.
3.Раскрытие неопределенностей, не относящихся к основным.
1. Важными результатами, связанными с понятием производной, являются теоремы о промежуточных значениях.
Теорема 1 (Ферма). Пусть функция f (x) определена на интервале (a,b) (где a – число или −∞, b – число или +∞) и в некоторой точке x0 этого
интервала принимает наибольшее или наименьшее значение. Тогда возможны только два случая:
1)f ′(x) = 0 ;
2)производная f ′(x) не существует.
Геометрический смысл случая 1) теоремы Ферма состоит в том, что касательная к графику функции y = f (x) в точке (x0 ; f (x0 )) параллельна оси Ox , если x0 – точка
максимума или минимума функции на интервале (a,b) (рис. 1)
Рис. 1. Геометрическая интерпретация случая 1) теоремы Ферма
Рис. 2. Геометрическая интерпретация случая 2) теоремы Ферма
Однако в точке максимума (минимума) x0 производная f ′(x0 ) может и не существовать. На рис. 2 представлен случай 2) теоремы Ферма. Здесь точки максимума и
