
2.5 Принцип неопределенности для частотно-временного представления сигнала.
На примере прямоугольного импульса покажем справедливость принципа неопределенности , состоящего в том, что невозможно одновременно локализовать импульс во времени и усилить его избирательность по частоте.
Согласно 5), ширина прямоугольного импульса во временной области DT равна 2Т. За ширину образа Фурье прямоугольного импульса примем расстояние между соседними нулями центрального горба в частотной области. Первые нули функции
![]() имеем при
имеем при
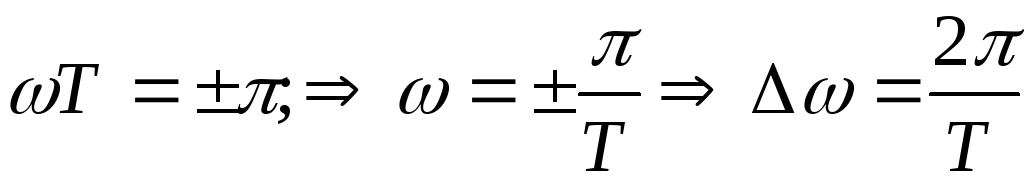 .
.
Таким образом получаем
![]() (8)
(8)
. Таким образом, чем более импульс локализован во времени, тем сильнее размазан его спектр. Обратно, чтобы сократить спектр, мы вынуждены растягивать импульс во времени. Этот принцип справедлив при любой форме импульса и носит универсальный характер.
2.6 Свертка и ее свойства.
Свертка-основная процедура при фильтрации сигнала.
Назовем функцию h(t) сверткой непериодических функций f(t) и h(t), если она определяется как следующий интеграл:
![]()
![]()
![]() (9)
(9)
Символически
будем обозначать этот факт как
![]() .
.
Операция свертки обладает следующими свойствами.
1. Коммутативность.
![]() (10)
(10)
Доказательство коммутативности можно получить путем замены переменной t-t=t’

2. Ассоциативность
![]() (11)
(11)
Доказательство:
Введя новую переменную t-t=p, далее меняя порядок интегрирования и делая замену переменной s-t+p=h, получим:

3. Дистрибутивность
![]() (12)
(12)
Доказательство этого свойства непосредственно следует из линейных свойств интегралов.
Для обработки сигналов наиболее важным в методе Фурье (после формул преобразования Фурье) являются теоремы о свертке. Будем использовать частоту n вместо w, т.к. теоремы о свертке в этом представлении будут иметь взаимообратимый характер.
2.7 Теоремы о свертке
Первая теорема о свертке.
Преобразование Фурье прямого произведения функций равно свертке преобразований
![]() ~
~
![]() (13)
(13)
Доказательство:
Пусть
![]() ,
тогда
,
тогда
![]() .
Используя определение обратного
преобразования Фурье и меняя порядок
интегрирования, получим:
.
Используя определение обратного
преобразования Фурье и меняя порядок
интегрирования, получим:

В терминах угловой частоты w эта теорема имеет менее универсальный вид
![]() ~
~
![]() (13а)
(13а)
Вторая теорема о свертке.
Преобразование Фурье свертки функций равно прямому произведению преобразований.
![]() ~
~
![]() (14)
(14)
Доказательство:

Для примера рассмотрим свертку прямоугольного импульса
![]()
По определению свертки нужно посчитать значение интеграла
![]() .
.
По условию f(t)=0 при t<-T и при t>T. Аналогично, f(t-t)=0 при
t-t<-T и при t-t>T, т.е. при t>t+T и при t<t-T. Поэтому при вычислении свертки бесконечные пределы можно заменить на конечные: нижний равен минимальному из двух значений (t-T) и -T, верхний равен минимальному из двух значений (t-T) и T. Рассуждая таким образом,получим
при 0<t<2T
![]()
при -2T<t<0
![]()
Объединяя оба случая, получим выражение для свертки:
![]()
Таким образом, сверткой прямоугольного импульса самого с собой будет треугольный импульс ( иногда эту функцию называют L-функцией).
Пользуясь теоремой о свертке , можно легко получить преобразование Фурье L-функции
![]() ~
~
![]() (15)
(15)
На практике физическим ситуациям соответствуют функции, равные нулю при t<0.Это приводит к тому , что бесконечные пределы заменяются конечными.
Пример:
Найти свертку функций f(t) и g(t)
![]()
![]()
Решение:
![]()
т.к. f(t)=0 при t<0 и g(t-t)=0 при t-t<0,т.е. при t>t.
Введем понятие взаимной корреляции двух функций f(t) и g(t).
![]() (16)
(16)
где t- временной сдвиг, непрерывно изменяющийся в промежутке (-¥,¥).
Важным понятием является корреляция функции с самой собой, которая носит название автокорреляции.
![]() (17)
(17)
