ГЛАВА

6

–––––––––––––––––––––––––––––––––––––––––––––––––––––

МАРТИНГАЛЬНЫЙ ПОДХОД

КОПРЕДЕЛЕНИЮ ЦЕН ОПЦИОНОВ

СПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ЭСШЕРА

§1. ПОНЯТИЕ О ПРЕОБРАЗОВАНИИ ЭСШЕРА

Внастоящей главе при предположениях о постоянной безрисковой процентной ставке показано, как можно определять эквивалентные мартингальные меры для довольно широкого класса стохастических моделей изменений цен активов. В частности, всякое преобразо-

вание Эсшера стохастического процесса { Х(t)} приводит к эквивалентной вероятностной мере для этого процесса, а вектор параметров преобразования выбирается таким, чтобы эквивалентная вероятностная мера являлась также мартингальной мерой для дисконтированной стоимости каждого лежащего в основе актива. Цена ФП вычисляется как математическое ожидание дисконтированного платежа по эквивалентной мартингальной мере. Другими словами, после соответствующего изменения вероятностной меры цена каждой ЦБ является просто актуарной настоящей стоимостью.

Преобразование Ф. Эсшера (Esscher, 1932) является проверенным временем инструментом финансовой математики. Здесь будет показано, что преобразование Эсшера является также эффективным методом для определения стоимости производных ЦБ, если логарифмы цен первичных ЦБ управляются определенными стохастическими процессами со стационарными и независимыми приращениями. Это семейство процессов включает процессы Винера и Пуассона, гамма-процесс и обратный процесс Гаусса. Преобразование Эсшера такого процесса цены акции индуцирует на процессе эквивалентную вероятностную меру, когда параметр Эсшера или вектор таких параметров определяется так, чтобы дисконтированная цена каждой первичной ЦБ являлась мартингалом при новой вероятностной мере. Тогда цена любой ФП вычисляется просто как математическое ожидание (по эквивалентной мартингальной мере) дисконтированных платежей. Прямые следствия метода преобразований Эсшера включают, среди прочего,

237

знаменитую формулу Блэка – Шоулса для определения цены опциона, известную биномиальную формулу цены опциона, формулы для определения цены опционов по максимуму и минимуму многократных рисковых активов и др.

Для плотности вероятностей f (х) пусть h будет вещественным числом таким, что существует

∞

M (h) = ∫ ehx f( x) dx.

− ∞

Функция переменной х

f (x; h) = ehx f( x) 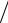M( h)

является плотностью вероятностей, и ее естественно назвать преобразованием Эсшера первоначального распределения с параметром h.

Преобразование Эсшера было разработано для аппроксимации распределения суммы совокупных выплат в окрестности точки х0 путем аналитических приближений рядами Эджворта к преобразованному распределению с параметром h, выбираемым так, чтобы новое среднее было равно х0. Когда преобразование Эсшера используется в задачах страхования для вычисления стоп-лосс премии, параметр h обычно находят путем определения среднего для преобразованного распределения как предела удержания.

Покажем, что преобразование Эсшера можно легко распространить на некоторые классы случайных процессов, которые включают некоторые из обычно используемых для моделирования изменений цен акций. Параметр h определяется так, чтобы модифицированная вероятностная мера была эквивалентной мартингальной мерой, по отношению к которой цены активов оказываются ожидаемыми дисконтированными платежами.

В качестве удачного применения метода преобразования Эсшера ниже выведена формула (6.10), которая является общим выражением для стоимости европейского опциона-колл на не выплачивающую дивиденды акцию. Как частный случай из нее получается формула Блэка – Шоулса для определения цены опциона, а также известные формулы для стоимости опциона с чистым скачком, биномиальная формула цены опциона и др. Из нее также следуют формулы для нетрадиционных моделей поведения цены акции таких, как гамма-процесс и обратный гауссовский процесс.

238

После этого метод преобразований Эсшера распространяется на случай определения стоимости ФП на пакеты рисковых активов. Основная схема анализа здесь следующая. Предположим, что свободная от риска процентная ставка является постоянной и обозначается через r. Пусть для t ≥ 0 S1(t), S2(t),…, Sn(t) обозначают цены n не выплачивающих дивидендов акций или активов в момент t. Предположим, что вектор

S1(t)

S2

(t)

Sn (t)

T

ln

(0) ,..., ln

S

(0) , ln

S

2

S

n

(0)

1

управляется стохастическим процессом, который имеет независимые и стационарные приращения, непрерывным по вероятности. Пусть g будет измеримой вещественной функцией n переменных. Тогда для

τ ≥ 0

Е*[е− δτ Sj (τ ) g (S1(τ ), S2(τ ),…, Sn(τ ))] = = Sj (0) Е**[g (S1(τ ), S2(τ ),…, Sn (τ ))],

где математическое ожидание в левой части вычисляется по нейтральному к риску преобразованию Эсшера, а математическое ожидание в правой части – по другому определенному преобразованию Эсшера. Будет показано, что многие классические формулы определения цен опционов являются прямыми следствиями этого результата.

Повсюду в этой главе безрисковая процентная ставка предполагается постоянной. Также предполагаем, что рынок является безынерционным и торговля производится непрерывно. Не имеется налогов, расходов на сделки и никаких ограничений на займы или короткие продажи. Все ЦБ совершенно делимы. Из результатов предыдущих глав понятно, что в такой модели рынка ЦБ отсутствие арбитража, по существу, эквивалентно существованию эквивалентной мартингальной меры, по отношению к которой цена случайного платежа является ожидаемой дисконтированной стоимостью. Некоторые авторы назы-

вают этот результат «фундаментальной теоремой определения цены актива». В общей постановке эквивалентная мартингальная мера не единственная. Преимущество нейтрального к риску преобразования Эсшера в том, что оно обеспечивает общее, прозрачное и однозначное решение. Далее мы используем некоторые основные идеи из теории стохастических процессов.

239

§ 2. НЕЙТРАЛЬНОЕ К РИСКУ ПРЕОБРАЗОВАНИЕ ЭСШЕРА

Для t ≥ 0 символ S (t) будет обозначать цену не выплачивающей дивиденды акции или ценной бумаги в момент t. Предполагаем, что имеется стохастический процесс { Х(t), t ≥ 0} , Х(0) = 0, со стационарными и независимыми приращениями такой, что

S(t) = S(0) ехр{ Х(t)} ,

t ≥ 0.

(6.1)

Для каждого t случайная величина Х(t), которую можно интерпретировать как непрерывно конвертируемую ставку доходности по t периодам, имеет неограниченно делимое распределение. Пусть

F (х, t) = рrоb [Х(t) ≤ х]

будет ее функция распределения, а

М(z, t) = Е[ехр{ z Х(t)} ]

является производящей функцией моментов (ПФМ). Путем предположения, что М(z, t) – непрерывная в точке t = 0, можно доказать, что

М(z, t) = [М(z, 1)]t.

(6.2)

Предположим, что (6.2) имеет место.

Для простоты примем, что случайная величина Х(t) имеет плот-

	ность	dF(x,t)
	f (x,t) =		,	t > 0,
		dx

тогда

∞

M (z,t) = ∫ ezx f( x, t) dx.

− ∞

Пусть h – вещественное число, для которого существует ПФМ М(h, t). Из равенства (6.2) следует, что если М(h, t) существует для одного положительного числа t, то она существует для всех положительных t. Теперь введем преобразование Эсшера с параметром h для процесса { Х(t)} . Оно также является процессом со стационарными и

240

независимыми приращениями, а новая плотность вероятностей процесса Х(t), t > 0, равна

f (x, t; h) =		ehx f (x, t)	=	ehx f (x, t)	.	(6.3)
	∞			M (h, t)
	∫ ehy f (y, t)dy
	−	∞

Это означает, что модифицированное распределение Х(t) является преобразованием Эсшера от первоначального распределения. Соответствующая ПФМ

	∞		M (z + h, t)
	M (z,t; h) = ∫ ezx f( x, t; h)	dx =		.
	− ∞		M (h, t)
	Из равенства (6.2) имеем

М(z, t; h) = [М(z, 1; h)]t.

(6.4)

(6.5)

Преобразование Эсшера скалярной случайной величины – хорошо известное понятие в литературе по теории риска. Здесь мы рассматриваем преобразование Эсшера случайного процесса. Другими словами, вероятностная мера процесса модифицируется. Поскольку экспоненциальная функция положительная, модифицированная вероятностная мера будет эквивалентной по отношению к первоначальной вероятностной мере; т. е. обе вероятностные меры имеют одни и те же множества меры нуль.

Мы хотим гарантировать, чтобы цены акций в модели были внутренне состоятельными. Поэтому ищем h = h* такое, чтобы процесс дисконтированной цены акции {S(t)ехр(− rt), t ≥ 0} являлся мартингалом по отношению к вероятностной мере, соответствующей значению параметра h*. В частности,

S(0) = Е*[S(t) ехр (− rt)] = Е*[S(t)] ехр (− rt),

где r обозначает постоянную безрисковую процентную ставку.

Из равенства (6.1) видно, что параметр h* является решением уравнения

1 = Е*[eX(t)] ехр (− rt),

или

ехр (rt) = М(1, t; h*).

(6.6)

241

Из равенства (6.5) видим, что решение не зависит от t, и мы можем положить t = 1:

ехр(rt) = М(1, 1; h*),	(6.7)
или
r = ln [М(1, 1; h*)].	(6.8)

Можно показать, что параметр h* является единственным. Доказательство этого будет приведено позже для более общего случая. Назовем преобразование Эсшера с параметром h* нейтральным к риску преобразованием Эсшера, а соответствующую эквивалентную мар-

тингальную меру – нейтральной к риску мерой Эсшера. Заметим, что хотя нейтральная к риску мера Эсшера единственная, эквивалентные мартингальные меры могут быть и другими.

Чтобы определить стоимость производной ценной бумаги (чьи будущие платежи зависят от эволюции цены акции), вычислим ожидаемую дисконтированную стоимость подразумеваемых платежей; ожидание берется по нейтральной к риску мере Эсшера. Рассмотрим европейский опцион-колл на акцию с ценой исполнения K и датой исполнения τ , τ > 0. Стоимость опциона в момент времени 0 равна

		Е* [(S(τ ) − K)+ ехр (− rt)] ,				(6.9)
где х+ = х, если х > 0, и х+ = 0, если х ≤				0.
Если определить
		k = ln[K /S(0)] ,
выражение (6.9) приобретает вид
		∞
		e− rτ ∫[S(0) ex − K] f( x, τ ; h *) dx =
		k
= e−	rτ S(0)∞∫ ex f (x, τ ; h*) dx −			e− rτ K[1− F(k, τ ; h*)].
		k
Из соотношений (6.3), (6.4) и (6.6) следует, что
ex f (x, τ ; h *) =		f (x, τ ) × exp{(h * + 1) x}		=	M (h * + 1, τ )	f (x, τ ; h * + 1) =
		M (h*, τ )			M (h*, τ )

= М(1, τ ; h*) f (х, τ ; h* + 1) = е r τ f (х, τ ; h* + 1).

242

Таким образом, стоимость европейского опциона-колл с ценой исполнения K и датой исполнения τ равна

S(0)[1 − F(k, τ ; h* + 1)] − е− r τ K[1 − F (k, τ ; h*)].

(6.10)

В дальнейшем эту общую формулу будем применять неоднократно. Будет показано, что формула (6.10) содержит, среди других, как частный случай знаменитую формулу Блэка – Шоулса для определения цены опционов.

В общем случае, когда функция распределения F (х, t) не обязательно дифференцируема, можно определить преобразование Эсшера через интегралы Стильтьеса, т. е. заменить равенство (6.3) на

dF(x, t; h) =		ehxdF(x, t)
	∞
	∫ ehydF(y, t)
	−	∞

ehxdF(x, t)

= ( ) . (6.11)

M h, t

(В своей статье Ф. Эсшер (Esscher, 1932) не предполагал, что функция распределения суммы индивидуальных выплат является дифференцируемой.) После такой замены формула (6.10) остается справедливой.

То, что условие отсутствия арбитража тесно связано с существованием эквивалентной мартингальной меры, было доказано ранее в главах 3 и 4. Эти результаты реализуют идею нейтрального к риску определения стоимости, использовавшуюся во второй части гл. 2. Более детально эти вопросы рассмотрены в книге Д. Даффи (Duffie, 1992). В модели дискретного времени отсутствие арбитражных возможностей эквивалентно существованию эквивалентной мартингальной меры. В более общей постановке характеризация более тонкая, и для строгости следовало бы заменить термин «эквивалентная» на «по существу эквивалентная».

Заметим, что формулу определения цены опциона (6.10) можно написать как

S(0) рrоb [S(τ ) > K; h* + 1] − е− r τ K рrоb [S (τ ) > K; h*].

где первая вероятность оценивается по мере преобразования Эсшера с параметром h* + 1, в то время как вторая вероятность вычисляется по отношению к нейтральному к риску преобразованию Эсшера. Обобщение этого результата дается в § 4.

243