19

Лекция 5. Оценка линейной статистической связи двух СВ. (из главы 8) (Читать до оценок)

Нормальное совместное распределение двух СВ

Матричное описание ковариационного эллипса

Нормальный закон в векторном виде

Геометрический смысл числа обусловленности ковариационной матрицы Cond

Ложная корреляция

Множественный коэффициент корреляции

8.4.2 Ковариационный эллипс и эллипсоид

8.4.2.1 Корреляционный эллипс как числовая характеристика

Теория статистической связи разработана выдающимся русским статистиком А. А. Чупровым (1874—1926) (“Основные проблемы теории корреляции” (1926) ).

Регрессия - термин, введенный английским статистиком Ф.Гальтоном (1822-1911) при изучении наследственности передачи роста родителей детям. Первоначальный смысл - констатация неполноты связи. Уравнение регрессии - это аналитическое уравнение, связывающее аргумент, который называют факторный признак, и функцию, называемую результативный признак. Коэффициент регрессии.

Корреляционное отношение η это корень квадратный из разности 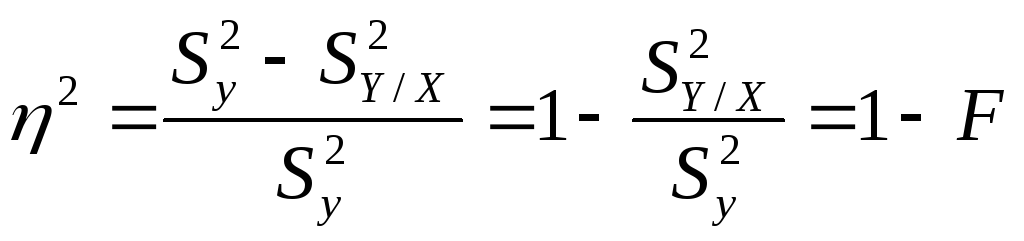. (7.17). Другое название – индекс корреляции γ. Показывает, насколько уменьшилась дисперсия

Нормальное совместное распределение двух СВ ( из 7.2.1.2. но не совсем так)

Фотограмметрия измеряет поверхности и объемы. Выполняют совместные измерения пар величин на снимке (x y), на модели – тройки (xyz), а на стереопаре – совместные измерения четверки (x y p q). Рассмотрим пару величин x и y. Закон распределения каждой из величин, конечно, может быть любой. Мы рассмотрим только нормальные. Величина x следует своему нормальному закону, а y - своему. Совместное воздействие двух законов приводит к тому, что положение точки на плоскости следует нормальному совместному распределению.

ФПВ совместного распределения (x y) выглядит так, как показано на рис. 1. Это «шляпа с плоскими полями», которые асимптотически прилегают к плоскости ХУ.. Объем под поверхностью, как и для распределения одной СВ, равен полной вероятности,т.е. единице.

На рис. видно, что при каждом заданном значении СВ x случайная величина y следует соответствующему нормальному распределению (и обратное: при каждом у свой норм закон у х). Если же х неслучайная величина, то распределение y не зависит от нее: оно будет одно и то же при любых значения х (образуется цилиндрическая поверхность с нормальной образующей). ФПВ совместного распределения двух СВ (вектора ) ,где , ; - нормирующий коэффициент (чтобы интеграл от -оо до +оо был равен единице); определитель ковариационной матрицы К.

Как видим, наряду с характеристиками рассеяния здесь появилась новая характеристика - ковариация.

Для чего нужна эта характеристика? Смотрим. У нас две СВ, значения которых появляются в один и тот же миг. Так как все в природе взаимосвязано, то и между ними существует связь. Слабая она или сильная (тесная) - случайная или очень тесная - функциональная - это другой вопрос, но связь существует всегда.

Ковариация (covariatia – совместное изменение) показывает тесноту статистической линейной связанности двух СВ. Так как мы всегда решаем системы линейных уравнений, то очевидно ее влияние на результат решения. Ее нужно оценивать и при обработке наблюдений учитывать. Неучет ковариаций приводит к несостоятельным оценкам дисперсий.

Рассмотрим эту числовую характеристику и ее оценку.

Отложим по осям ±_х и ±_у. Образуется прямоугольник 2_x * 2_y. Если _x⁼ _y, то будет квадрат – «щит для мишени». Проведем горизонтальное сечение «шляпы» плоскостью так, чтобы оно прошло через точки пересечения вертикальных линий от ±_х и ±_у с поверхностью ф.п.в. Сечение образует - эллипс (при _x = _y = круг на мишени). Так как эллипс соединяет точки с равной плотностью вероятности для ±_х и ±_у, то он, по сути, равнозначен стандарту для одиночной величины, вероятность появления коей в пределах стандарта . Однако, здесь, даже при отсутствии корреляции, вероятность попадания точки внутрь эллипса, при нормальном законе распределения очень- очень приближенно составит. (С удалением точки от центра по оси Х или У максимум плотности вероятности уменьшается. Сечение поверхности в этой точке оси есть ф.п.в. Она с удалением становится все более плоской, т.е плотность вероятности, убывая по оси Х, убывает и поу при данном х )

Как видим, величины центрированы и нормированы. Поэтому стандарт этих дробей равен единице. Прямоугольник есть квадрат. Форма эллипса, вписанного в квадрат, может изменяться от круга до линии, соответственно и его площадь - от максимальной для круга до нуля (линия).

Ковариация – второй смешанный центральный момент, есть характеристика формы эллипса: , где и . Оценка ковариации вычисляется по формуле оценки смешанного момента .

Если задача состоит в том, чтобы выявить только наличие связи, то вычисляют смешанный начальный момент без учета к средних (x_{ср ,} y_ср) .

Если нужно оценить силу статистической связи, т.е. какая из пар величин теснее связана, то ковариацию, нормируют стандартами. Нормированную стандартами ковариацию называют коэффициентом линейной корреляции, _. Оценка этого коэффициента .

Свойства коэффициента линейной корреляции: (1) -1<r<1

При r, близком к нулю, его распределение близко к нормальному. С увеличением |r| распределение его оценок асимметрично. При плюс- минус единице -это импульсы. Для нахождения доверительного интервала оценки r, вычисленной по данным наблюдениям, переходим к величине Фишера , которая распределена нормально. Ее дисперсия зависит от объема n, а именно . Поэтому сначала находим границы доверительного интервалаtS_z этой величины, а затем lделаем обратный переход от граничных значений z к граничным значениям r.

В пределах доверительного интервала полагают r незначащим. Если r вышел за границы доверительного интервала, то он значим, и можно составить линейное уравнение – регрессии .

Геометрический смысл коэффициента корреляции: программа 2мернN-распр., рисунки для r -1 <0 >0 1 (в главе 8)

Матричное описание ковариационного эллипса. Ковариационная матрица , где корреляционная матрицаR описывает направление большой полуоси корреляционного эллипса и его сжатость

Нормальный закон в векторном виде для вектора X^т=[xy]^т запишется так или .

В общем виде для любого вектора

{f(x)=(1/[2*p*s1*s2*(1-r^2)^1/2])*e^(-1/2*(1-r^2)*[(x-m1)/s1]^2+[(y-m2)/s2]^2 - 2*r*[(x-m1)/s1]*[(y-m2)/s2]}

Геометрический смысл числа обусловленности ковариационной матрицы Cond(K). Естественно, что при |r|<1 ковариационная матрица, как и любая квадратная невырожденная матрица, имеет отличные от нуля собственные числа, по которым можно оценить ее обусловленность.

В последующем рассмотрим нормальное многомерное распределение. Там показано, что оси ковариационного эллипсоида определяются собственными значениями ковариационной матрицы с точностью до постоянного для всех осей коэффициента. Поэтому Cond(K). показывает отношение большей оси эллипсоида рассеяния вектора к наименьшей оси этого же эллипсоида.

Применительно к ковариационной матрице это число характеризует коррелированность элементов вектора , так как собственные числа функции суть функции коэффициентов корреляции. Например, для двухмерного вектора:, где, v(X)- вероятность)

Отсюда коэффициент корреляции , а обусловленность.

Ложная корреляция. Если случайный вектор содержит более двух величин, то корреляционная матрица содержит все парные коэффициенты корреляции, образующие сочетания i c j, Тогда одна из величин может влиять порознь на вторую и третью с одним знаком. Получается мнимое впечатление и (мнимый коэффициент корреляции), что эти две последние непосредственно связаны между собою. Это влияние называют ложная корреляция. Для ее выявления используют частный коэффициент корреляции параметров i и j (ЧКК). Его вычисляют так:

где -минор элемента r _ij корреляционной матрицы R_p, -минор i-ой единицы, а - j-ой единицы главной диагонали этой матрицы. Он показывает линейную корреляцию в чистом виде данной пары элементов.

Примечание. Если _j минор матрицы , то ему будут соответствовать элемент матрицы N. Тогда: , ибо, что упрощает вычисление коэффициентов.

Если ЧКК меньше парного коэффициента, то ложная корреляция присутствует

В фотограмметрии ложная корреляция существует для вычисленных значений ЭвзО ₁ ₂ и ₂

Коэффициент множественный корреляции величины y с вектором X

Коэффициент множественной корреляции вычисляется так r_y,X= (1- D/My) ^0.5, где M_y -минор параметра y; D- определитель корреляционной матрицы R_p. Он равен нулю только тогда, когда все r=0.

Отсутствие линейной корреляции еще не говорит о независимости результатов. Может существовать корреляционная зависимость второго и более высокого порядка.

Заметить нелинейную корреляцию можно, построив график для серии пар значений двух случайных величин. Если по расположению точек на графике можно заметить характер кривой, т.е. видна нелинейная корреляция, то подбирают формулу этой кривой для перехода от этой кривой к прямой. Стремятся, чтобы параметров было меньше, т.е. чтобы число степеней свободы было больше.

Качество кривой оценивают по дисперсии уклонений от нее и оставшемуся числу степеней свободы, используя критерий Фишера (по дисперсионному (в геодезии) отношению или по критерию Фишера.) Вы такое решение проделаете на примере аппроксимации профиля местности полиномами

.

Ниже повтор: подробное изложение

8.4.2. Ковариационный эллипс и эллипсоид . Найдем элементы корреляционного эллипса : большую и малую полуоси a и b и угол наклона  большой полуоси к оси (v₁/s₁), (без множителей). Для этого решаем вековое уравнение корреляционной матрицы , где -определитель матрицы; -след матрицы R.. Из теории решения уравнений второго порядка известно, что сумма корней равна коэффициенту при первой степени (следу матрицы), а произведение - свободному члену (ее определителю), т.е. Отсюда -Полуоси эллипса соответственно суть (8.68)

где для нормального распределения,инварианты кривой второго порядка.

Теперь найдем угол наклона a большой полуоси к оси : .

Отсюда . При отрицательном значении коэффициента корреляции (r<0) знак  изменится на противоположный.

Следовательно, для нормированных величин эллипс привписан в квадрат 2х2. Его большая полуось может занимать два фиксированных положения (см. рис.8.1), точнее, знакr определяет, какая из полуосей больше. При для нормированных уклонений полуоси стремятся к радиусу=1 , а эллипс к окружности (рис.8.3).

При ненормированных уклонениях v₁ и v₂ угол можно найти по общей формуле .

При , малая полуось стремится к нулю, эллипс сплющивается, вырождаясь в диагональ.

8.4.2.1 Корреляцонный эллипс как числовая характеристика

Корреляционный эллипс есть характеристика двухмерной с.в. Он, аналогично числовой характеристике рассеяния одномерной с.в., служит внешней границей рассеяния с.в. при заданной доверительной вероятности . Внутри эллипса лежит, грубо оценивая, менеевсех ее значений.

Точнее, вероятность наблюдения случайного вектора X^т =[XY] внутри корреляционного эллипса, вписанного в прямоугольник со сторонами 2s₁ и 2s₂ при (т.е. одномерная вероятность v(X)= v(Y)=0.678) равнагде W - область интегрирования, ограниченная эллипсом.

Для эллипса, вписанного в прямоугольник со сторонами 4s₁ и 4s₂ при (т.е. v(X)=0.678) вероятность попадания в эллипс равна 0.865,. а 3 сигма -0.989 Приэта доверительная вероятность всегда стремится к нулю.

Соответственно для трех-, четырех-,...n-мерной с.в. (т.е. случайного вектора) эллипсу будет соответствовать эллипсоид. Внутри трех-, четырех-,..., n-мерного эллипсоида находится <<ⁿ-я доля всех значений случайного вектора.

Это видно из наглядных рассуждений. Возьмем 2s₁ = 2s₂ =2_. Такое положение достигается нормированием координат их стандартами. Тогда площадь квадрата 2*2=4, а площадь эллипса, принявшего форму окружности, - , будет наменьше, т.е.вероятность составит,что близко к интегральному значению 0.39.

Из гл 8 пояснения. Покажем, что при определенных условиях кривая есть эллипс. Сравнивая кривую с каноническим уравнением кривой второго порядка , найдем ее форму.

Значения коэффициентов будут следующие , где .

Для исследования кривой найдем ее инварианты ,и.

__________________

Примечание. От латинского margo - край, межа, граница - маргинальное = крайнее.

Здесь С= ln{2πs₁s₂(1-r²)^1/2 v(X)} логарифм нормирующего множителя нормального распределения,

а v(X) это, см. выше, заданная вероятность

Известно, что кривая второго порядка есть при

A0 эллипс при AI<0 действительный;

D>0 при AI>0 мнимый;

A=0 пара мнимых прямых; A0 гипербола; ?

===================================================

D<0

A=0 пара действительных прямых; A0 парабола;

D=0

A=0 пара действительных прямых.

Так как в (8.66) D>0 ибо (|r|<1), а AI=4(1-r²)^1/2C<0 ибо (C<0; (1-r²)>0), то кривая (8.57) в данном случае есть действительный эллипс. Этот эллипс называют корреляционным.

3. Случайные величины зависимы. Рассмотрим предельный случай, когда r стремится к единице. Инварианты (8.66) при |r|=1, будут A=0*(-); D=0; AI=0*(-).

Раскроем неопределенность. Введем обозначение 1-r²=y. Тогда при |r|1 y0, а инвариант A из (8.66) перепишется так: A=2y ln(2ps₁²s₂² f(x)y)=y² ln k y. здесь при y0 ln ky-.

Для разрешения неопределенности применим правило Лопиталя, так как обе функции на отрезке [0,1] непрерывны, .

Таким образом, . Поэтому эллипс вырождается в пару совмещенных действительных прямых (дляr=1 и r=-1). Отсюда немедленно следует, что объем цилиндра под поверхностью функции плотности вероятности, образующая которого есть корреляционный эллипс, вырождается в одну из плоскостей для r=1 или r=-1).

Для многомерного вектора - n-мерный объем вырождается в (n-1)-мерный. Если из n величин будет r зависимых, то имеем поверхность размерности n-r.

Двумерное распределение случайного вектора вырождается в одномерное- случайной величины.

DIXI. КОНЕЦ

Полное изложение вопроса