10.2. Критерий Фишера

Для проверки гипотезы Н_о используют функцию выборки. Эта функцию называют статистикой, лежащей в основе критерия.

Задаваясь уровнем значимости q (или доверительной вероятностью ), с помощью этой функции находим граничное значение статистики, т.е. такое критическое значение, которое ограничивает доверительную область.

По выборке в свою очередь находим эмпирическое значение этой же статистики. Если это значение лежит внутри доверительной области, то считается, что с вероятностью  данные этой выборки не противоречат нулевой гипотезе. Если же эмпирическое значение превышает граничное, т.е. попадает в критическую область, то Н_о отвергается.

Безусловно, здесь могут быть ошибки

первого рода: Н_о отвергается, хотя она истинна. Отвергается (1-).

второго рода: Н_о принимается, хотя она ложна.

Критерий тем лучше, чем меньше вероятность ошибки второго рода. Действительно, отвергнув Н_о, мы продолжим проверку, подходят ли другие Н₁, ..., Н_к, но приняв Н_о, мы тем самым отказываемся от рассмотрения других гипотез.

В дисперсионном анализе в качестве такой статистики Р. Фишер предложил применять отношение дисперсий , причем для однозначности в знаменателе ставят меньшую дисперсию:.

Если измеряемая величинаx_i подчиняется нормальному распределению, то показатель степени распределения следует распределению² с r степенями свободы. Тогда отношение дисперсий есть распределению Фишера. Функция плотности вероятности распределения Фишера f = f(F,r_1,r₂) зависит как от статистики F, так и от степеней свободы r₁ большей (числитель) и r₂ меньшей (знаменатель) дисперсии.

Так как распределение ² исходит из нормального, а распределение Фишера - из ² , то, как видим, исходное требование для этой статистики состоит в том, чтобы выборка (любая) была распределена нормально.

Если по какой-либо причине это условие не соблюдено, то искусственно делают приближение к нормальному закону при помощи некоторой монотонной функции. Такими приближениями могут служить, например такие преобразования: x=(x')^0.5, X=(x')^-1 , x=A log(x'+B) и т. п.

10.3. Одно и двухфакторной дисперсионный анализ. (написал заново по лаб.раб70-х. т.к. не нашел главы, главное нумерация формул?!

Рассмотрим однофакторный и двухфакторный дисперсионный анализ

10.3.1. Однофакторный дисперсионный анализ

Как явствует из названия, здесь выявляется влияние одного фактора.

Рассмотрим два варианта: серии в выборке имеют (1) равные и (2) неравные количества наблюдений.

10.3.1.1. Равночисленные наблюдения в сериях

Постановка задачи в общем виде состоит в следующем.

Дано. Имеется m независимых нормально распределенных величин x_i, каждая из которых наблюдалась n раз. В результате получили выборку x_ij из mn наблюдений, где i=1, 2,…, m; j=1,2, …, n.

Задача. Проверяется нулевая гипотеза , согласно которой центры распределения величин x_i равны, то есть . Предполагается, что все x_i выполнены с одним стандартом σ. Всего имеется mn наблюдений (m строк i, n столбцов j).

Решение.

Обозначим среднее арифметическое изi-й серии наблюдений (строка i):

Средние каждой серии будут различаться вследствие как случайных погрешностей наблюдений, так и вследствие влияния исследуемого фактора. Для оценки значимости этого различия поступаем так.

Вычисляем общее среднее из mn наблюдений .

Находим общую эмпирическую дисперсию по известной формуле .

Находим дисперсию, обусловленную влиянием фактора и дисперсию, какая останется после исключения влияния этого фактора, т.е. остаточную.

Для нахождения дисперсий: факторной и остаточной разложим сумму в формуле общей дисперсии по частным средним: .

Учитывая, что , ибо одна и та же разность суммируетсяj раз, а , так как это сумма отклоненийi-ой серии от среднего в этой же серии, получаем .

Умножим и разделим первое слагаемое на m(n-1), второе на (m-1):

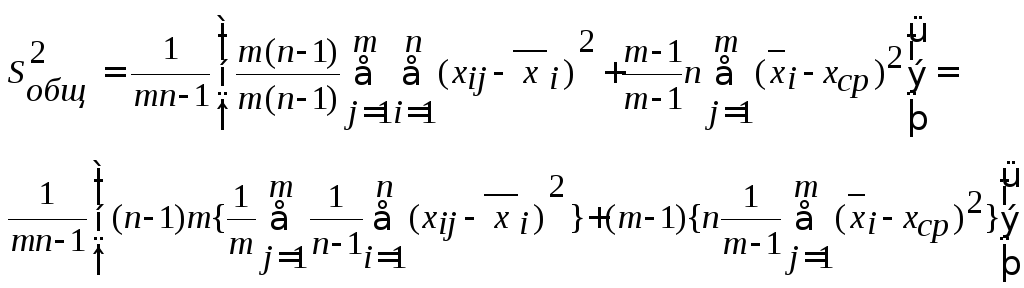
В первых фигурных скобках заключена дисперсия, из которой исключили влияние фактора (конечно, в той мере в какой оно компенсировалось усреднением по i). Она названа остаточной .

Во вторых - дисперсия средних, увеличенная в n раз. Она названа факторной .

Итак, мы разложили общую дисперсию на две составляющие .

Если выполняется т.е. все их оценки , а мы обоснованно полагаем, что все наблюдения выполнялись с равной точностью, то факторная дисперсия будет отличаться от нуля только вследствие случайных погрешностей и ограниченности выборки.

Но непосредственно приравниватьинельзя. Хотя каждое наблюдение используется как при вычислении, так и, однако вдля формирования общего среднего идет доля каждого наблюдения, равнаяx_ij/mn, а для – на частные средние - уходит x_ij/n. Поэтому несмещенной оценкой выборки служит , как более надежная, которая следует распределению χ² с r=(mn-1) степенями свободы