61. 11.2. Рациональные дроби: правильные и неправильные. Простейшие рациональные дроби

Определение 1. Рациональной дробью или дробно-рациональной функцией называется отношение двух многочленов , где- многочлен степени, а- многочлен степени.

Определение 2. Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя: .

Определение 3. Рациональная дробь называется неправильной, если степень числителя не меньше степени знаменателя.

Если дробь неправильная, то выделяют её целую и правильную части путем деления числителя на знаменатель уголком:

,

Простейшими рациональными дробями называются дроби четырех типов: 1) ; 2);

3);

4) , где.

Коэффициенты .

63. 11.3. Разложение правильной алгебраической дроби на сумму простейших

Теорема. Всякую правильную рациональную дробь можно разложить на сумму простейших дробей единственным образом.

Вид разложения правильной рациональной дроби на сумму простейших зависит от корней знаменателя.

Пусть рациональная дробь имеет вид , при этом возможны такие ситуации.

1) Все корни знаменателядействительные и простые:. В этом случае правильная рациональная дробь представляется в виде суммы дробей первого типа следующим образом:, где

Пример. .

2) Корни – действительные, причем некоторые из них кратные, тогда,и правильная рациональная дробь представляется в виде суммы дробей первого и второго типа:

.

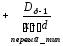Пример. .

3) Среди корней есть комплексно-сопряженные простые корни, то есть, тогда каждому квадратному трехчлену с отрицательным дискриминантом соответствует дробь третьего типа:

4) Среди корней знаменателя есть комплексно-сопряженные кратные корни, то есть . В этом случае рациональная дробь представима в виде суммы дробей первого, второго, третьего и четвертого типов.

Замечание. Коэффициенты разложения правильных рациональных дробей на сумму простейших дробей находят методом неопределенных коэффициентов, который заключается в том, что сумма правых частей разложения с неизвестными коэффициентами приводится к общему знаменателю, а затем приравниваются числители левой и правой частей. Составляются уравнение или система уравнений, в которых приравниваются коэффициенты при соответствующих степеняхx слева и справа. Приравнивать коэффициенты начинают со степеней х, на единицу меньших степени знаменателя исходной правильной рациональной дроби.

Пример.

.

Чтобы определить неизвестные коэффициенты, приравняем коэффициенты при одинаковых степенях х , начиная со второй степени:

64. Лекция 12. Линейные пространства

12.1. Определение линейного пространства, свойства линейных пространств. Примеры линейных. пространств

12.2. Подпространство линейного пространства

12.3. Линейно зависимые и независимые векторы. Базис и размерность линейных пространств

12.4. Евклидово пространство. Ортогональная система векторов. Процесс ортогонализации

12.5. n- мерное арифметическое пространство Rn. Скалярное произведение n-мерных векторов, длина вектора. Угол между n-мерными векторами

66. 12.1. Определение линейного пространства, свойства линейных пространств. Примеры линейных пространств

Определение. Непустое множество Е элементов любой природы Е = { x, y, z, t, … } называется линейным или векторным пространством над полем действительных чисел R , если выполняются следующие условия:

а) имеется правило, посредством которого любым двум элементам х, у множества Е ставится в соответствие элемент z этого же множества Е, называемый суммой этих элементов : z = x + y;

b) имеется правило, посредством которого каждому элементу х множества Е и любому действительному числу λ ставится в соответствие элемент u = λ x , называемый произведением х на λ .

При этом указанные правила ( операции ) удовлетворяют восьми аксиомам:

1. x + y = y + x - коммутативное ( переместительное ) свойство суммы ;

2. ( x + y ) + z = x + (y + z ) - ассоциативное ( сочетательное ) свойство суммы;

3. Существует нулевой элемент 0 Є Е такой, что х + 0 = х для любого элемента х Є Е ;

4. Для любого элемента х Є Е существует противоположный элемент (- х ) Є Е такой, что х + ( - х ) = 0 ;

5. Для любых действительных чисел α и β верно равенство α(βх) = (αβ)х - ассоциативное относительно числового множителя свойство ;

6. 1∙х = х для любого элемента х Є Е ( особая роль числового множителя 1 );

7. Для любого действительного λ и произвольных элементов х, у Є Е выполняется равенство λ ( х + у ) = λ х +λ у - дистрибутивное (распределительное) относительно суммы элементов свойство;

8. Для любых действительных чисел α и β и произвольного элемента хЄ Е верно равенство (α + β ) х = α х + β х - дистрибутивное (распределительное) относительно суммы числовых множителей свойство.

Свойства линейных пространств

Теорема 1. В произвольном линейном пространстве Е существует единственный нулевой элемент 0 Є Е , и для любого элемента х Є Е существует единственный противоположный элемент ( - х ) Є Е.

Теорема 2. В произвольном линейном пространстве Е:

1. Нулевой элемент равен произведению любого элемента х Є Е на число 0 ;

2. Для любого элемента х противоположный элемент (-х ) равен произведению этого элемента х на число -1 : ( - х ) = ( - 1 ) х.

Примеры линейных пространств

1. Множество всех алгебраических многочленов степени, не превышающей натурально го числа n. Легко убедиться, что если х и у - многочлены степени не выше n,то они будут обладать свойствами 1 – 8 ;

2. Множество геометрических векторов пространства R², исходящих из начала координат;

3. Множество всех матриц одного и того же размера m×n с введенными в нем операциями сложения матриц и умножения матрицы на число . В этом множестве нулевая матрица будет нулевым элементом. Матрица, полученная из матрицы А умножением всех ее элементов на число ( - 1), будет являться для матрицы А противоположным элементом ;

4. Множество всех функций, непрерывных на отрезке [ a , b ], с поточечными для функций операциями сложения и умножения на число.

5. Множество всех функций вида αе^t+be^-t, где α иb – произвольные вещественные числа.

Примеры множеств, не являющихся линейными пространствами

1. Множество всех алгебраических многочленов степени, точно равной натуральному числу n. В этом множестве не определена операция сложения элементов, так как сумма двух многочленов может оказаться многочленом степени ниже n.

2. Множество многочленов степени не выше n с положительными коэффициентами. В этом множестве не определена операция умножения элемента на число: такие многочлены нельзя умножать на отрицательные числа.

3. Множество геометрических векторов на плоскости, исходящих из начала координат, концы которых расположены в первой четверти. В таком множестве не определена операция умножения на отрицательные числа.