
- •Содержание
- •Лекция 1. Матрицы и определители n-го порядка.
- •1.1. Матрицы, их виды, линейные операции над матрицами
- •1.2. Умножение матриц
- •1.3 Определителиn-го порядка и их свойства
- •1.4. Обратная матрица
- •Лекция 2. Системы линейных уравнений и их решение
- •2.1. Системыmлинейных уравнений сnнеизвестными. Основные понятия
- •2.2. Решение системnлинейных уравнений сnнеизвестными по формулам Крамера
- •2.3. Решение системnлинейных уравнений сnнеизвестными матричным способом
- •2.4. Решение системmлинейных уравнений сnнеизвестными методом Гаусса
- •2.5. Ранг матрицы. Теорема Кронекера-Капелли
- •2.6. Однородные системы
- •Лекция 3. Решение матричных уравнений
- •Замечания.
- •1) При решении необходимо определить тип матричного уравнения и метод его решения.
- •3.2. Собственные векторы и собственные значения матрицы
- •3.3. Модель Леонтьева многоотраслевой экономики
- •Лекция 4. Векторы на плоскости и в пространстве
- •4.1. Векторы и линейные операции над ними
- •1) ; 2)Если;
- •3) Если; 4)
- •4.2. Проекция вектора на ось
- •4.3. Скалярное произведение векторов
- •4.4. Векторное произведение векторов
- •4.5 Смешанное произведение векторов
- •Лекция 5. Координатный метод
- •5.1. Системы координат на плоскости
- •5.2.Системы координат в пространстве
- •Лекция 6. Уравнения прямой и плоскости в пространстве
- •6.1. Плоскость в пространстве
- •6.2. Прямая в пространстве
- •6.3. Взаимное расположение прямой и плоскости в пространстве
- •Лекция 7. Прямая линия на плоскости
- •7.1. Уравнения прямой на плоскости
- •7.2. Взаимное расположение прямых на плоскости
- •Лекция 8. Линии второго порядка и поверхности второго порядка
- •8.1. Кривые второго порядка. Основные понятия
- •8.2. Поверхности второго порядка
- •Лекция 9. Теоретико-множественные понятия в математике
- •9.1. Понятие множества. Круги Эйлера. Операции над множествами
- •9.2. Отношения и отображения как соответствия между элементами множеств. Мощность множества
- •9.3. Множество действительных чиселRи его основные подмножества
- •9.4. Окрестность точки, элементы топологии
- •Лекция 10. Действительные и комплексные числа
- •10.1. Действительные числа и их основные свойства
- •10.2. Определение комплексных чисел, комплексная плоскость, формы записи комплексных чисел
- •10.3. Операции с комплексными числами
- •Лекция 11. Многочлены
- •11.1. Многочлены. Разложение многочленов на множители
- •11.2. Рациональные дроби: правильные и неправильные. Простейшие рациональные дроби
- •11.3. Разложение правильной алгебраической дроби на сумму простейших
- •Лекция 12. Линейные пространства
- •12.1. Определение линейного пространства, свойства линейных пространств. Примеры линейных пространств
- •12.2. Подпространство линейного пространства
- •12.3. Линейно зависимые и независимые векторы. Базис и размерность линейных пространств
- •12.4. Евклидово пространство. Ортогональная система векторов. Процесс ортогонализации
- •Лекция 13. Линейные операторы
- •13.1. Определение линейного оператора и его основные свойства. Линейное пространство операторов, действующих из х в у
- •13.2. Свойства линейных операторов, действующих из х в х. Определение обратного оператора. Условие обратимости линейного оператора
- •13.3. Матрица линейного оператора
- •13.4. Переход к новому базису. Матрица перехода и её основные свойства. Связь координат вектора и матриц линейного оператора при переходе к новому базису
- •13.5. Собственные векторы и собственные значения линейного преобразования
- •13.6. Линейная модель обмена
- •Лекция 14. Квадратичные формы
- •14.2. Поведение квадратичной формы при линейном преобразовании переменных
- •14.3. Приведение квадратичной формы к каноническому виду
- •14.4. Свойства канонических форм. Знакоопределенность
- •Лекция 15. Математические структуры
- •15.1. Понятие структуры
- •15.2. Алгебраические структуры: группы и полугруппы, подгруппы, кольца и поля
- •15.3. Матричные алгебраические структуры
- •Рекомендуемая литература
2.4. Решение системmлинейных уравнений сnнеизвестными методом Гаусса
Рассмотрим
систему вида:

Метод Гаусса состоит в последовательном исключении неизвестных и в приведении системы к ступенчатому виду путём элементарных преобразований.
Элементарными преобразованиями системы называют преобразования вида:
- перестановка местами любых двух уравнений системы;
- умножение обеих частей уравнения на число, отличное от нуля;
- прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на одно и то же число.
В
результате элементарных преобразований
получается система, эквивалентная
исходной. Если при проведении элементарных
преобразований получается уравнение
вида
 ,
то такое уравнение вычёркивается из
системы. Если получается уравнение
вида
,
то такое уравнение вычёркивается из
системы. Если получается уравнение
вида ,
где
,
где ,
то система несовместна.
,
то система несовместна.
Переход от исходной системы (1) к равносильной системе ступенчатого вида называется прямым ходом метода Гаусса, а нахождение переменных из системы ступенчатого вида – обратным ходом.
Прямой ход
В
системе среди коэффициентов при
неизвестном x1
найдётся хотя бы один не равный нулю.
Уравнение с этим коэффициентом
записывается первым.
 –
ведущий коэффициент для первого
уравнения. Разделим первое уравнение
системы наa11,
получим:
–
ведущий коэффициент для первого
уравнения. Разделим первое уравнение
системы наa11,
получим:
 ,
где
,
где
Проведём первый шаг преобразований, который заключается в исключении неизвестной x1 из 2-го, 3-го… уравнений системы. Для этого будем умножать уравнение (4) на числа –a21, –a31…–am1 и складывать соответственно со 2-м, 3-м,…, m-м уравнениями системы (1).
В
результате получим систему:
 .
.
Второй шаг преобразований.
Предположим
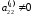 –
ведущий коэффициент 2-го уравнения
системы (5). Разделим обе части 2-го
уравнения системы (5) на
–
ведущий коэффициент 2-го уравнения
системы (5). Разделим обе части 2-го
уравнения системы (5) на ,
полученное уравнение
,
полученное уравнение ,
где
,
где С помощью уравнения (6) исключим неизвестнуюx2
из 3-го, 4-го, …, m-го
уравнений системы (5). Для этого умножим
обе части уравнения (6) на числа
С помощью уравнения (6) исключим неизвестнуюx2
из 3-го, 4-го, …, m-го
уравнений системы (5). Для этого умножим
обе части уравнения (6) на числа
 и сложим соответственно с 3-м, 4-м, …,m-м
уравнениями системы.
и сложим соответственно с 3-м, 4-м, …,m-м
уравнениями системы.
В
результате получим систему:
 .
.
После конечного числа таких шагов возможны варианты.
Получена система треугольного вида:
 которая
совместна и определенна. Она имеет
единственное решение, которое находится
обратным ходом.
которая
совместна и определенна. Она имеет
единственное решение, которое находится
обратным ходом.
Получена система трапецеидального вида. Тогда выбираются базисные неизвестные
 ,
которые выражаются через свободные
неизвестные
,
которые выражаются через свободные
неизвестные ,
и записывается общее решение системы.
В этом случае система имеет бесконечное
множество решений в зависимости от
значений свободных неизвестных.
,
и записывается общее решение системы.
В этом случае система имеет бесконечное
множество решений в зависимости от
значений свободных неизвестных.
Система несовместна, если она содержит уравнение вида
 ,
, .
.
Пример.
Решить систему уравнений
 методом Гаусса.
методом Гаусса.
Решение


Ответ:
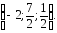
2.5. Ранг матрицы. Теорема Кронекера-Капелли
Определение. Рангом матрицы называется наивысший порядок не равного нулю её минора. Минор порядка равного рангу матрицы и отличный от нуля называется базисным (таких миноров у матрицы может быть несколько).
Правило вычисления ранга матрицы
Ранг матрицы равен максимальному числу ненулевых строк после приведения её к ступенчатому виду путём элементарных преобразований.
Определение. Элементарными преобразованиями матрицы называются преобразования вида:
перестановка местами любых двух строк (столбцов) матрицы;
умножение всех элементов строки (столбца) на число, отличное от нуля;
прибавление к элементам одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число;
транспонирование;
вычёркивание строки, все элементы которой равны нулю.
Теорема. При элементарных преобразованиях ранг матрицы не меняется.
Пример. Найти ранг матрицы.


Рассмотрим
систему вида:
 Введём основную матрицу системы
Введём основную матрицу системы ,
составленную из
,
составленную из
коэффициентов при неизвестных и расширенную матрицу системы
 .
.
Теорема
Кронекера-Капелли.
Для того чтобы система m
линейных уравнений с n
неизвестными была совместна, необходимо
и достаточно, чтобы ранг основной матрицы
системы был равен рангу расширенной
матрицы этой системы, то есть
 .
.
Замечание.
1.
Если
 ,
то система несовместна;
,
то система несовместна;
2.
Если
 ,
то система определённая;
,
то система определённая;
3.
Если
 ,
то система неопределённая. В этом случае
по базисному минору выписывают уравнения,
в которых базисные переменные выражаются
через свободные неизвестные и записывается
общее решение системы уравнений.
,
то система неопределённая. В этом случае
по базисному минору выписывают уравнения,
в которых базисные переменные выражаются
через свободные неизвестные и записывается
общее решение системы уравнений.
