Квантовая физика

Кислов А.Н.					Атомная физика
напряженности			магнитного поля. Во-вторых, частица за счет взаимодей-
		H
ствия магнитного момента с магнитным полем					H приобретет дополни-
тельную энергию U, равную
					(6.8)
			U H H cos .
В этом случае энергия Е частицы будет вычисляться по формуле
			Е = Ео + U .
Необходимо подчеркнуть, что энергия U зависит не только от величин и
H векторов		и	H , но и от угла α между их направлениями. Причем энер-
гия U добавляется к энергии Ео, когда векторы и					H ориентированы в раз-

ные стороны, и вычитается, когда они ориентированы в одном направлении.
Допустим, что ось z направлена так же, как вектор	H , т.е.	H	= (0, 0, Н),

тогда

Поскольку проекция

z

U cos H

магнитного момента

z H .
	на ось z квантуется (6.7), то

энергия Е частицы в магнитном поле может принимать только дискретные значения. Например, для электрона, обладающего магнитным орбитальным

моментом l , имеем
E Eo lz H Eo gl b ml H .	(6.9)

Энергетические уровни, которые до наложения магнитного поля были вырожденными по квантовому числу ml, при наличии поля расщепляются на (2l+1) подуровней в соответствии с числом возможных значений ml, т.е. снимается вырождение по этому квантовому числу.

На рис. 6.2 схематически показано расщепление энергетических уровней электрона в водородоподобном атоме. Расстояние между соседними энергетическими подуровнями, согласно (6.9), равно b Н.

Рис. 6.2

ГОУ ВПО УГТУ-УПИ 2005

Стр. 101 из 142

Кислов А.Н. Атомная физика

Для проверки существования пространственного квантования в 1922 г. физиками Штерном и Герлахом был проведен опыт по изучению расщепления пучка нейтральных атомов серебра, проходящего через область с неод-

нородным магнитным полем. Отметим, что в неоднородном поле на атом с

магнитныммоментом (он не зависит от координат) действует сила

F	gradU grad( H ) H

,

которая приводит к изменению конфигурации пучка атомов, т.е. его расщеплению на отдельные компоненты. В однородном поле происходит только

			атомов и никакие силы, действующие
ориентировка магнитных моментов
на атом, не возникают,		следовательно, пучок расщепляться не будет.
Установка, используемая в опы-
тах Штерна и Герлаха, схематично
изображена на рис. 6.3. Пучок ато-
мов серебра, имеющих один валент-
ный электрон, который находится в
невозбужденном s-состоянии, т.е.
обладает	магнитным	орбитальным
моментом	l , равным нулю, направ-
ляется в область, где полюсами S и N
магнита создается неоднородное по-
ле в направлении, перпендикуляр-
				Рис. 6.3
ном движению пучка.		Затем пучок

попадает на пластинку П. На этой пластинке можно обнаружить следы от

осевших атомов. Полюс S имеет форму «ножа», благодаря чему под ним от-

лична от нуля только z-я составляющая магнитного поля: H = (0, 0, Н(z)).

Поэтому на атомы, двигающиеся вблизи полюса S вдоль оси y, действует си-

ла Fz, направленная по оси z и пропорциональная z-й составляющей	z маг-
	z :
нитного момента атомов и неоднородности магнитного поля H (z)

	F				H (z)
		z		z	z

.

Эта сила вызывает расщепление пучка атомов вдоль оси z на столько компо-

нент, сколько возможных проекций z имеет магнитный момент .

В опытах Штерна и Герлаха на пластинке от осевших атомов серебра наблюдали две полоски, расположенные симметрично относительно начального направления движения пучка атомов. Это свидетельствовало о том, что в присутствии магнитного поля проекция z может принимать два значения,

ГОУ ВПО УГТУ-УПИ 2005

Стр. 102 из 142

Кислов А.Н. Атомная физика

одинаковых по величине и противоположных по знаку. Таким образом, опыт подтвердил существование пространственного квантования. Кроме того, в

опытах Штерна и Герлаха была вычислена величина проекции	z	магнитно-
го момента атома серебра, равная одному магнетону Бора b .

Однако в то время возникли трудности при объяснении результатов опыта Штерна и Герлаха на основе квантовой теории. В опытах наблюдали расщепление пучка только на две компоненты. Из теории следовало, что если пучок состоит из атомов с валентным электроном, находящимся в невозбужденном s-состоянии (l = 0), т.е. атомов, обладающих магнитным орби-

тальным моментом	l , равным нулю, то пучок в магнитном поле не должен

расщепляться, так как сила, действующая на атомы, равна нулю. Если валентный электрон атома находится в р-состоянии (l = 1), то пучок должен расщепиться на три компоненты в соответствии с квантовым числом ml,

определяющим число возможных проекций	lz	магнитного орбитального
момента l .

Эта проблема была преодолена после того, как в 1925 г. Гаудсмит и Уленбек для объяснения структуры спектров сложных атомов (атомов, имеющих более одного электрона) выдвинули гипотезу о том, что электрон об-

ладает собственным моментом количества движения		, который назвали
	s

спином. Спин не связан с движением электрона в пространстве, упрощенно, его можно связать с вращением электрона вокруг своей оси. Спин электрона

	квантуется по обычным правилам.		Для величины		спина справедливо
s				s
следующее равенство:
			s(s 1) ,		(6.10)
	s

где s – это спиновое квантовое число. полняется такое равенство:

s	z

Для проекции sz спина

ms ,

s

на ось z вы-

(6.11)

где ms – это магнитное спиновое квантовое число. Оно принимает (2s + 1) значения от –s до s через 1 и характеризует ориентацию спина s и возмож-

ные значения его проекции sz относительно оси z.

Кроме этого, электрон обладает еще и магнитным спиновым моментом

s

:

			e
s s s		g s		s	,	(6.12)
			2mc

ГОУ ВПО УГТУ-УПИ 2005

Стр. 103 из 142

Кислов А.Н.	Атомная физика

	где	s g s	e	– спиновое гиромагнитное отношение.
			2mc

Правила квантования для магнитного спинового момента

s

имеют вид

			s	s(s 1) g s
	s	s s

	sz		s	s	z		s	m		s
Отметим, что с учетом спина
											s
новой Ψ-функцией вида
						(r, s)

	e
			s(s 1) g s b			s(s 1) ,		(6.13)
	2mc
	g s	e		ms g s b ms .				(6.14)
		2mc

состояния электрона описываются вол-

n,l,m	(r, , ) m	s	.
l

Таким образом, различные стационарные состояния электрона в атоме характеризуются четырьмя квантовыми числами: n, l, ml и ms, причем, кратность вырождения n-го уровня электрона, находящегося в кулоновском поле ядра водородоподобного атома, равна уже 2n2.

Вернемся к рассмотрению опыта Штерна и Герлаха. В этом опыте ато-

мы пучка имели валентный электрон, обладающий только магнитным спи-

новыммоментом s . Из того факта, что пучок в магнитном поле распадался

на две компоненты, следовало, что проекция Sz магнитного спинового мо-

мента s могла принимать только два значения, поэтому число возможных

значений для ms равно двум: (2s + 1) = 2. Следовательно, спиновое квантовое число s для электрона равно 1/2: s = 1/2, а магнитное спиновое квантовое число ms принимает следующие два значения: ms = ± 1/2.

Кроме того, в опытах Штерна и Герлаха была вычислена величина про-

	Sz
екции		магнитного спинового момента	s , равная одному магнетону

Бора b . Отсюда следует, что фактор g s = 2 и спиновое гиромагнитное отношение s в два раза больше орбитального гиромагнитного отношения l :

s 2 .

l

ГОУ ВПО УГТУ-УПИ 2005

Стр. 104 из 142

Кислов А.Н.	Атомная физика
6.3. Полный механический момент электрона,
полный и эффективный магнитные моменты.
Внутреннее и магнитное внутреннее квантовые числа.
	Фактор Ланде
	электрона необходимо рассматривать уже его пол-
При учете спина s

ный момент количества движения				j , равный векторной сумме орбитального
	и собственного		момента электрона:
l		s
				j l			(6.15)
						s .

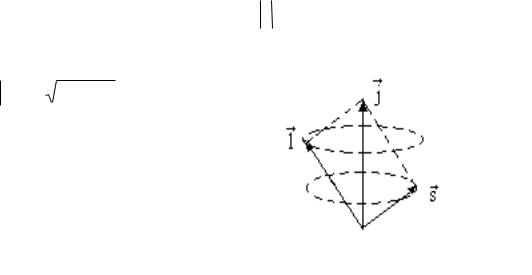
Причем векторы		и		прецессируют
	l		s
(рис.6.4).

Полный момент количества движения ной, а правила квантования для его длины соответственно вид

			j( j 1)	,	(6.16)
j

вокруг направления вектора
		j
	является квантованной величи-
j
j	и проекции jz на ось z имеют

где j – это внутреннее квантовое число, которое может принимать значения j = l s,..., l s ;

j	z	m	j

,

(6.17)

Рис. 6.4

где mj – это значения mj

магнитное внутреннее квантовое число. Оно принимает (2j + 1)
= –j,…,j через 1, характеризуя ориентацию вектора		и возмож-
	j

ные значения проекции jZ относительно оси z.

Правила отбора для внутреннего j и магнитного внутреннего mj квантовых чисел следующие:

j = 0, ± 1 , mj = 0, ± 1 .

Отметим, что когда учитывается взаимодействие орбитального l и соб-

ственного s моментов электрона, то различные стационарные состояния

электрона в атоме характеризуются такими четырьмя квантовыми числами:
n, l, j и mj. Это связано с тем, что из-за прецессии векторов l		и s относи-
тельно направления вектора	j их проекции lz и sz на ось z не сохраняются
ГОУ ВПО УГТУ-УПИ 2005	Стр. 105 из 142

Кислов А.Н.	Атомная физика

постоянными, в то время как

j

и jz являются постоянными величинами. Ес-

ли взаимодействие орбитального		и собственного		моментов электрона не
	l		s

учитывается, как, например, в случае наличия сильного внешнего магнитного поля, тогда проекции lz и sz сохраняются постоянными и стационарные состояния электрона в атоме характеризуются уже другими квантовыми чис-

	лами: n, l, ml и mS.
	Аналогично сложению орбитального		и собственного		моментов
		l		s

электрона происходит сложение и соответствующих магнитных моментов

	l										ï
		и s , в результате которого получается полный магнитный момент j
	электрона:
		ï
		j l s .									(6.18)
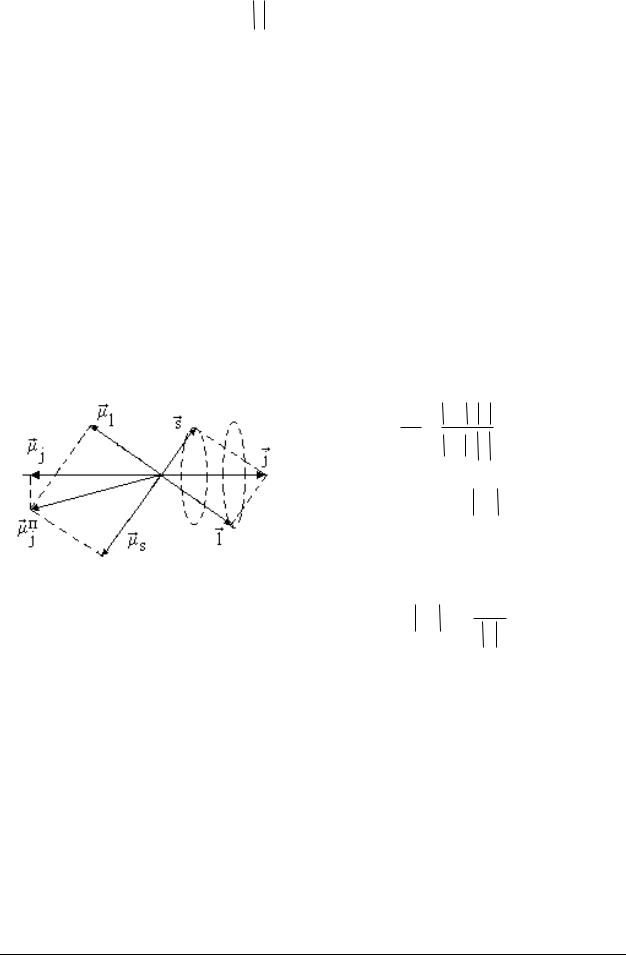
		Векторная диаграмма всех моментов, связанных с электроном в атоме,
			ï
	представлена на рис. 6.5. Вектор			непараллелен вектору							j . Это обуслов-
			j
	лено тем, что
						s			s	/ s	2 .
					l
										/ l
									l

Рис. 6.5

Величина проекции	j	вектора

прямую, на которой лежит вектор числяется по формуле

		ï
			j
		j
j		.
		j



j

ï j

,

на

вы-

Соответствующий этой проекции вектор

j

называется эффективным маг-

нитным моментом электрона и характеризует его поведение в магнитных

полях. Эффективный магнитный момент j				связан с полным моментом ко-
личества движения	j :
		e
	j g j		j	,	(6.19)
		2mc

где g j – это фактор (множитель) Ланде. Причем выполняются следующие равенства:

ГОУ ВПО УГТУ-УПИ 2005

Стр. 106 из 142

Кислов А.Н.	Атомная физика

		g	e	j( j 1)
	j		j
			2mc

			g		e	m
		jz		j	2mc		j

g	j		b	j(

g		m	j
j	b

j 1)

.

,

(6.20)

(6.21)

Найдем фактор Ланде		g j . Исходим из того,
нитного момента j	справедливо выражение

что для эффективного маг-

						ï
				j		j	j	j
	j		j
				j		j		j

.

Учитывая (6.18), (6.12) и (6.5), запишем

ï				e
						gl	l	g s
j			2mc							s
						1		2
поэтому
				e	(l
								2s ) j
	j									j
				2mc			j	2
							g
								j

,

.

Сравнивая это выражение с (6.19), видим, что

l j

g j

2sj

.

2

j

Учитывая (6.15), приведем

g j

к виду

2

2

g j

l (l s )

2s (l

s )

l

2s

3l s

.

2

2

j

j

Поскольку из (6.15) следует, что

2l s

j

2

l

2

s 2 ,

то для g j получим

ГОУ ВПО УГТУ-УПИ 2005

Стр. 107 из 142

Кислов А.Н.	Атомная физика

				2		2		2			2	2			2
			3 j				l			j				l
g					s				1			s
	j					2							2
					2 j							2 j

.

Заменяя квадраты векторов их значениями (6.3), (6.10), (6.16), придем к окончательному результату:

	g j 1	j( j 1) s(s 1) l(l 1)	.	(6.22)
		2 j( j 1)
	Из полученного выражения видно, что фактор Ланде		g j	зависит от кванто-
	вых чисел j, l и s.

6.4. Спин-орбитальное взаимодействие. Тонкая структура спектра

Ранее было показано, что собственными значениями уравнения Шредингера (5.4) для водородоподобного атома являются значения Еn, зависящие только от главного квантового числа n. При этом необходимо отметить, что

уравнение Шредингера, во-первых, является нерелятивистским, во-вторых, не учитывает наличие спина s у электрона.

Уравнение, учитывающее релятивистскую зависимость массы электрона от скорости и наличие у него спина s , было предложено в 1928 г. Дираком.

Уравнение Дирака дает более сложную формулу для энергии Еnj электрона водородоподобного атома, которая зависит как от главного квантового числа n, так и от внутреннего квантового числа j. Это происходит за счет того, что к энергии Еn прибавляются дополнительные слагаемые Еnl и Еnjls. Вклад Еnl учитывает изменение массы электрона в зависимости от его скорости, а

вклад Еnjls – наличие у электрона спина s :

E	nj	E	n	E	nl	E	njls

.

Энергетические уровни Еnj называются уровнями тонкой структуры. Квантовые переходы между такими уровнями определяют в спектрах излучения или поглощения структуру, называемую тонкой структурой спектра.

Рассмотрим, как изменится энергия электрона водородоподобного ато-

ма только за счет учета у него спина s , т.е. найдем значение Еnjls. Это значение найдем из следующих полуклассических соображений. В системе от-

счета, связанной с электроном, ядро, вращаясь вокруг электрона, создает

магнитное поле с напряженностью H l. С этим магнитным полем, обусловленным орбитальным движением ядра вокруг электрона, взаимодействует

ГОУ ВПО УГТУ-УПИ 2005

Стр. 108 из 142

Кислов А.Н.	Атомная физика

магнитный

называется

спиновый момент

спин-орбитальным

	e		электрона. Это взаимодействие
s	mc	s
взаимодействием. Энергия				U sl , которую

электрон приобретает за счет спин-орбитального взаимодействия, вычисляется по формуле

U sl s H l .

Напряженность H l магнитного поля в месте нахождения электрона равна
			1			1
		H l	c	E v		cm	E p ,
		– это скорость и импульс электрона соответственно. Напряжен-
где v	и p
ность электрического поля E ,			создаваемого ядром на электроне, выражается
через силу		F , действующую на электрон со стороны ядра или потенциаль-

ную энергию U электрона:

Следовательно,

U sl

		1 gradU(r)
E F					1 dU r .
	e		e		e dr r

	e		1	1 dU				1			1 dU
	mc	s			dr	r	p	2	c	2	r dr
							m
			cme r

sl

.

(6.23)

Из этой формулы видно, что спин-орбитальное взаимодействие можно
трактовать как взаимодействие спинового		и орбитального
	s		l моментов.

Энергия U sl спин-орбитального взаимодействия зависит от ориентации маг-
нитного спинового момента s электрона относительно напряженности маг-
нитного поля H l или ориентации спина	s	электрона относительно его орби-
тального момента количества движения	l	, которую характеризует магнитное

спиновое квантовое число ms. У энергетических уровней

(En Enl ) , вы-

рожденных по квантовому числу ms, спин-орбитальное взаимодействие снимает это вырождение. Оно изменяет энергию (En Enl ) электрона и явля-

ется причиной расщепления этих энергетических уровней.

Формула (6.23) получена для неинерциальной системы, связанной с ускоренно двигающимся электроном. В 1926 г. Томас и Френкель показали, что при переходе к системе отсчета, связанной с ядром, в выражении для Usl появляется множитель 1/2. Кроме того, если считать, что движение электро-

ГОУ ВПО УГТУ-УПИ 2005

Стр. 109 из 142

Кислов А.Н.	Атомная физика

на осуществляется в кулоновском поле ядра с зарядом +ze водородоподобного атома и его потенциальная энергия равна

U

следовательно,

dU dr

а также учесть, что

zer2

ze2 r 2

,

,

		1		2
s l			j
		2

		2
	l

2 s

,

то выражение для энергии преобразовать к виду

U sl

спин-орбитального взаимодействия можно

U sl

							j
	1	ze		2
								2
	4 m	2	c	2	r	3

		2
	l

2 s

.

(6.24)

Наблюдаемая энергия (En Enl

в эксперименте ) электрона за

величина Еnjls, на которую изменяется счет спин-орбитального взаимодействия,

равна среднему значению <Usl> энергии спин-орбитального взаимодействия

U sl	в состоянии, описываемом волновой функцией Ψnlm:
	Еnjls = <Usl> = ∫ Ψ*nlm Ûsl Ψnlm dτ ,

где интегрирование производится по координатному пространству; Ψnlm –

это функция, описывающая состояния электрона с энергией (En Enl ) и не
	у электрона.
учитывающая наличие спина s
Из формулы (6.24) для U sl	видно, что при вычислении	Еnjls	необходи-
мо найти среднее значение <1/r3 >, а также средние значения		< j2	>, < l 2 > и

	2	>	квадратов операторов полного		2 , орбитального
< s				j

моментов. Cреднее значение <1/r3 > равно

m3 e6 z3

<1/r3 > = —————————— .

		2
	l

2

и спинового s

ħ6 n3 l ( l + 1/2 ) ( l + 1 )

ГОУ ВПО УГТУ-УПИ 2005

Стр. 110 из 142