Квантовая физика

Кислов А.Н.				Атомная физика
Предположим, что частица переместилась из точки с потенциалом элек-
трического поля	o	в точку с потенциалом	1	(рис. 1.3), тогда, введя раз-

ность потенциалов как V = o – 1

, получим выражение

mv	2		mv
1
2			2

2 o

qV

(в системе CГСЭ и СИ). (1.9а)

Если разность потенциалов V измеряется в вольтах (В), а m, v и q в единицах системы CГСЭ, то применяется следующая формула:

mv	2		mv
1
2			2

2 o

		qV
		300

.

(1.9б)

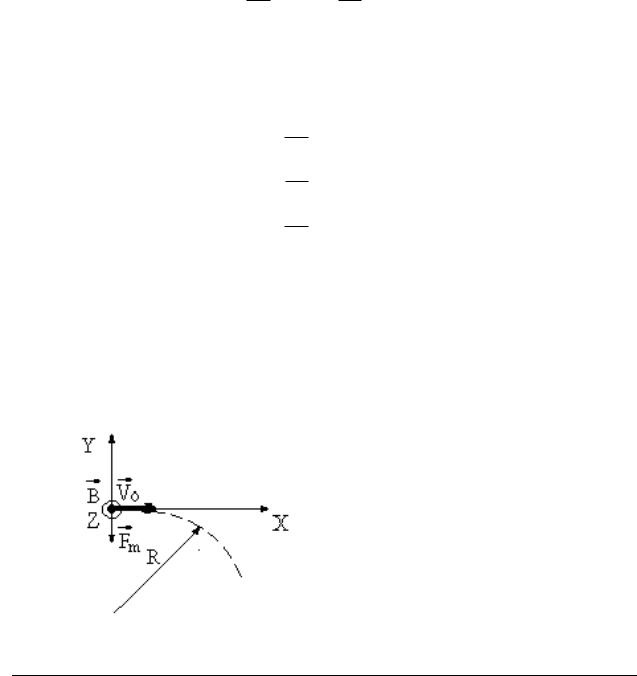
Пусть частица движется в электростатическом поле, силовые линии ко-

торого перпендикулярны вектору начальной скорости частицы vo . Считаем,
	что направление координатной оси	х
	совпадает с направлением вектора v o	, а
	начало координат совпадает с точкой
	влета частицы в поле (рис. 1.4). Тогда
	E = (0,Е,0) ,
	v o = ( vo ,0,0) ,
Рис. 1.4	ro = (0,0,0) .

Для этого случая имеем три скалярных уравнения:

	x 0 ,
		q
			E	,
y		m
	z 0 .

Если их дважды проинтегрировать по времени t, то получим следующие уравнения (с учетом начальных условий):

		x(t) vo t ,
			q
				Et 2
	y(t)				,
			2m
		z(t) 0 .

ГОУ ВПО УГТУ-УПИ 2005

Стр. 11 из 142

Кислов А.Н.	Атомная физика

Из первых двух уравнений этой системы легко найдем уравнение траектории частицы в плоскости у(х):

y( x )	q	E	x 2	.	(1.10)
	2m		vo2

Видно, что траекторией является парабола.

Исследуем движение заряженной частицы в магнитном поле. В этом случае E = 0, а уравнение движения для нее имеет вид

i

j

k

..

q

q

B

v

v

v

r

v

x

y

z

mc

mc

B

B

B

x

y

z

.

(1.11)

Это векторное уравнение эквивалентно системе трех скалярных уравнений:

		v			q	v		B		v
			x		mc		y		z
					q
						v		B		v
	v		y				z		x
					mc
						v
	v				q			B		v
			z				x		y
					mc

z

x

y

B B B

y

z

x

 

, , .

(1.12)

Интегрирование данной системы уравнений в большинстве случаев представляет трудную математическую задачу, поэтому рассмотрим простой случай: поперечное магнитное поле относительно начальной скорости ча-

стицыvo .

Пусть вектор индукции B магнитного поля, в котором движется части-

ца, направлен вдоль оси z декартовой системы координат, а вектор началь-

ной скорости частицы v o перпендикуля-

рен вектору B и направлен вдоль координатной оси x. Причем частица начинает двигаться из начала координат (рис. 1.5). Можно написать

B= (0,0,В) ,

v o = ( vo ,0,0) , ro = (0,0,0) .

Рис. 1.5

ГОУ ВПО УГТУ-УПИ 2005

Стр. 12 из 142

Кислов А.Н.	Атомная физика

Отметим, что на частицу с
ставляющая		силы Лоренца
	Fm

зарядом q будет действовать магнитная со- Fë , направление которой можно определить

по правилу левой руки.

Для заряженной частицы верна следующая система уравнений:

v

q

v

B

v

,

x

mc

y

c

y

q

v x B

c v x

v y

mc

,

0

v z

,

(1.13)

где ввели обозначение

c

qB mc

, которое называется циклотронной частотой.

Из третьего уравнения системы (1.13) с учетом начальных условий следует, что z-я компонента скорости vz равна нулю.

Дифференцируя по времени t два первых уравнения системы (1.13), получим систему однородных дифференциальных уравнений второго порядка с постоянными коэффициентами:

v		2 v	x	,
	x	c
		2 v .
v
	y	c	y

Решение этих уравнений ищем в виде vx = ekt и vy = ekt соответственно. Тогда для них имеем k1,2 = ±iωc, поэтому получается следующая система уравнений:

v	x	C	cos	t C	2	sin	t	.
		1	c			c
v y		C3	cos c t C4			sin c t

Учитывая первые два уравнения системы (1.13), находим, что С2 = С3 = 0, С1 = –С4. Из начальных условий следует, что С1 = vo. Таким образом, имеем

			cos c t ,
vx vo
		v		sin		t .
v	y		o		c

ГОУ ВПО УГТУ-УПИ 2005

Стр. 13 из 142

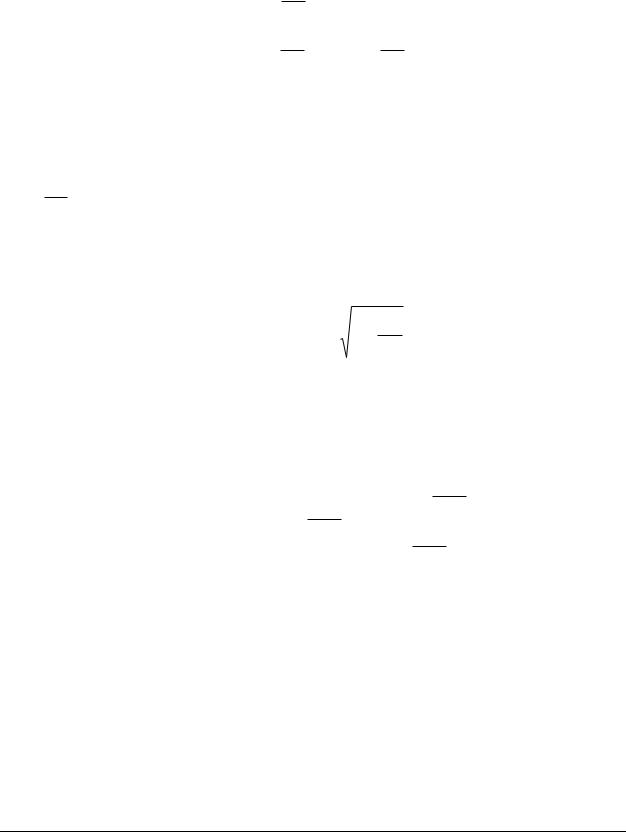
Кислов А.Н.	Атомная физика

Интегрирование этих уравнений по времени t позволяет прийти к системе параметрических уравнений, определяющих положение частицы в пространстве в зависимости от времени t (с учетом начальных условий):

		v
	x(t)	o		sin		t	,
					c
			c
		vo		cos c t				vo		,
y(t)
			c						c
	z(t) 0 .

Данная система задает окружность, по которой движется частица, радиуса

		v
	R	o	на плоскости у(х) (рис. 1.5).
		c

Рассмотрим случай малого отклонения частицы, т.е. R >> (y(t),х(t)), и найдем уравнение траектории частицы на плоскости у(х). Можно написать, что

		x	2
y(x) R R	1
			2
		R

где первое слагаемое возникает из-за того, что ратный корень в ряд Маклорена по степеням x2

,

ro

до

= (0,0,0). Разложим квадвторого члена:

							x
							2
	x	2		2R
y(x) R R(1							2R
				)
	2R		2			x	2
						2R

.

Из рис. 1.5 видно, что верным является нижнее решение, следовательно, траекторией будет парабола

y(x)	q		B		x 2	.	(1.14)
	2m c vo

.

ГОУ ВПО УГТУ-УПИ 2005

Стр. 14 из 142

Рис. 1.6

Кислов А.Н. Атомная физика

1.3. Определение электрического заряда электрона

Исторически первым было определено отношение заряда электрона к его массе, а не сама величина заряда электрона, поэтому рассмотрим вначале экспериментальный метод, использовавшийся в опыте Томсона для определения удельного заряда электрона.

Опыт Томсона учитывает закономерности движения электрона в электрическом и магнитном полях. Отметим, что отклонение частицы в поперечном электрическом поле зависит не только от отношения ее заряда q к массе m, но и от квадрата величины ее скорости v2 – см. (1.10), а в поперечном магнитном поле – от величины скорости v – см. (1.14). Поэтому измерение отклонения в каком-либо одном поле не позволяет найти отношение заряда q к массе m частицы.

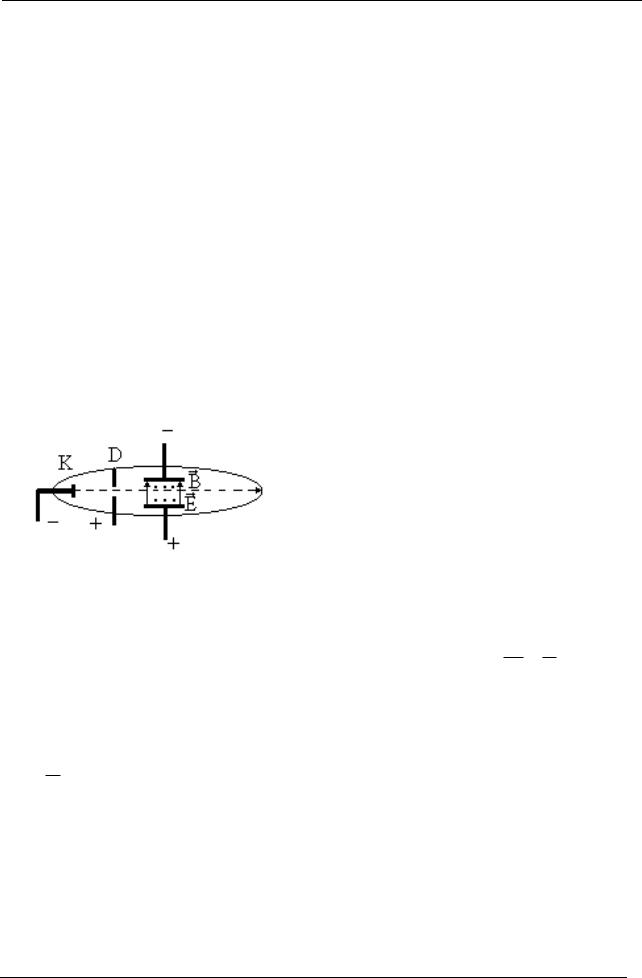
В опыте Томсона измеряли отклонение узкого пучка катодных лучей
(электронов), коллимированных диафрагмой D и проходящих через скре-
щенные поперечные электрическое	E и магнитное		B поля (рис. 1.6). Элек-
	троны, попадая на стекло, вызывают
	люминесценцию, видимую глазом. От-
	метим, что отклонение, связанное с
	этими электрическим и магнитным по-
	лями, будет происходить вдоль одного
	направления.
	В	начале	подбирается напряжен-
	ность	E электрического поля таким об-

разом, чтобы отклонение, обусловленное этим полем, компенсировало отклонение, связанное с магнитным полем, из-за чего пучок не отклонялся бы.

В этом случае из выражений (1.10) и (1.14) следует, что

E vo

B c

. Отсюда

можно определить начальную скорость vo электронов. Затем, выключив магнитное поле и измерив отклонение пучка лишь в одном электрическом поле, вычислют удельный заряд электрона. Результаты измерений показали,

что

e	5	17
m		10

ед. CГСЭ/г.

Рассмотрим экспериментальный опыт Милликена, используемый для определения величины заряда электрона. В этом опыте проводилось прямое измерение заряда медленно испаряющихся маленьких капелек масла (диаметром порядка 1 микрона) путем наблюдения за их движением в электрическом поле.

В пространстве между обкладками конденсатора, расположенными на

расстоянии d друг от друга, создается электрическое поле напряженности E .

ГОУ ВПО УГТУ-УПИ 2005

Стр. 15 из 142

Кислов А.Н.	Атомная физика

Через отверстие в верхней пластине конденсатора впрыскиваются капли масла (рис. 1.7). При пульверизации отдельная капля масла приобретает заряд q. На каплю в конденсаторе действуют следующие силы:

	сила тяжести			4	R3			, где R – ра-
		mg				m	g
				3
	диус капли, ρm –		плотность масла; подъ-

Рис. 1.7

емная

где ρv – плотность воздуха; сила трения

сила	Архимеда
			Fa
F тр 6 Rv		, где η –

	4		3
		R		v g	,
	3

коэффициент

вязкости воздуха, Лоренца qE .

v

– скорость капли; электрическая составляющая силы

Через некоторое время капля под действием этих сил будет двигаться равномерно, поэтому уравнение движения капли имеет вид

	4	R3 (
			m		v	)g	6 Rv	qE 0 .
	3

Изменяя полярность на пластинах конденсатора (при неизменной величине напряженности E поля), измеряем скорость падения v1 и скорость подъема

v2 капли. В результате получается система двух уравнений. Например, для скорости падающей капли имеем уравнение

		2R	2	(				)g		qE
v					m		v
1					9					6 R

.

Если из уравнения для v1 вычесть уравнение для v2, то приходим к формуле для определения радиуса капли:

	3	(v		v	2		)
R			1
	2	(						)g
			m			v

,

а если уравнения сложить, тогда получим формулу для определения заряда капли:

q 3 R(v1 v2 ) . E

ГОУ ВПО УГТУ-УПИ 2005

Стр. 16 из 142

Кислов А.Н.	Атомная физика

Измерения заряда q капли показали, что он всегда кратен одному и тому же числу е, которое следует считать величиной элементарного заряда и которое равно е = 4,8·10-10 ед. CГСЭ.

1.4. Основы релятивистской динамики частицы

а. Зависимость массы частицы от ее скорости

Как отмечалось ранее, зная отношение заряда частицы к ее массе, а также величину заряда, можно вычислить массу частицы. В 1901 г. Кауфман, проводя экспериментальные исследования зависимости удельного заряда

электрона

e m

от его скорости v, обнаружил, что при скоростях v, близких к

скорости света с, существует зависимость массы от скорости. Таким образом, еще за четыре года до появления теории относительности, которая объясняет такую зависимость, было получено экспериментальное доказательство отмеченного факта.

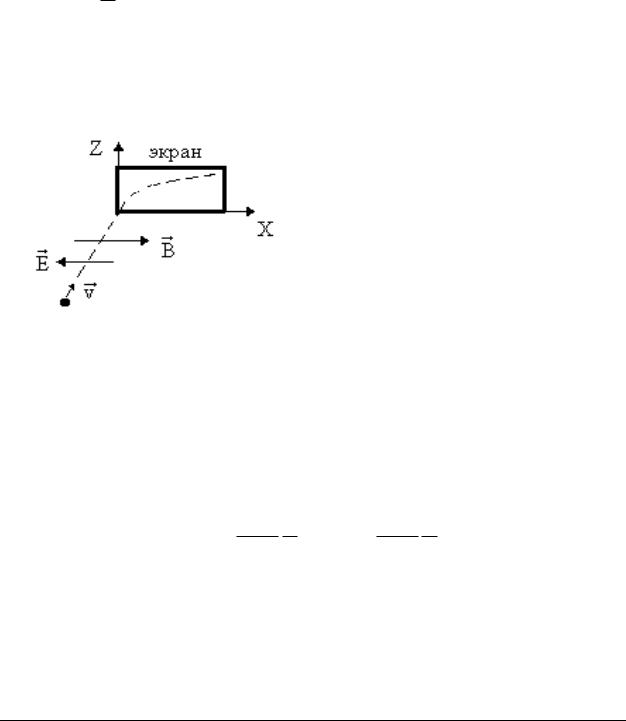
	В опыте Кауфмана, так же как
	и в опыте Томсона, учитывались
	закономерности движения	элек-
	трона в электрическом и магнит-
	ном полях. В качестве источника
	быстрых электронов использовался
	радий (радиоактивное вещество).
	Электроны, летящие со скоростью
	v, пропускаются через располо-
Рис. 1.8	женные антипараллельно друг дру-
	гу поперечные электрическое	E и
	магнитное B поля (рис. 1.8).

Отметим, что отклонения электронов, вызываемые электрическим и магнитным полями, будут происходить в перпендикулярных направлениях. Отклонение электронов в электрическом поле происходит в положительном направлении оси х, а в магнитном поле – в положительном направлении оси z. Величины отклонения электронов на экране равны соответственно

xý

const

v2

e m

,

	z			const	e
		ì		v	m

.

Поскольку разные электроны имеют различные скорости v, то места попадания их на экран расположатся на некоторой кривой. Если бы масса электронов не зависела от скорости, то этой кривой была бы парабола:

ГОУ ВПО УГТУ-УПИ 2005

Стр. 17 из 142

Кислов А.Н.	Атомная физика

	z		2		e
		ì		const
	x				m
			ý

.

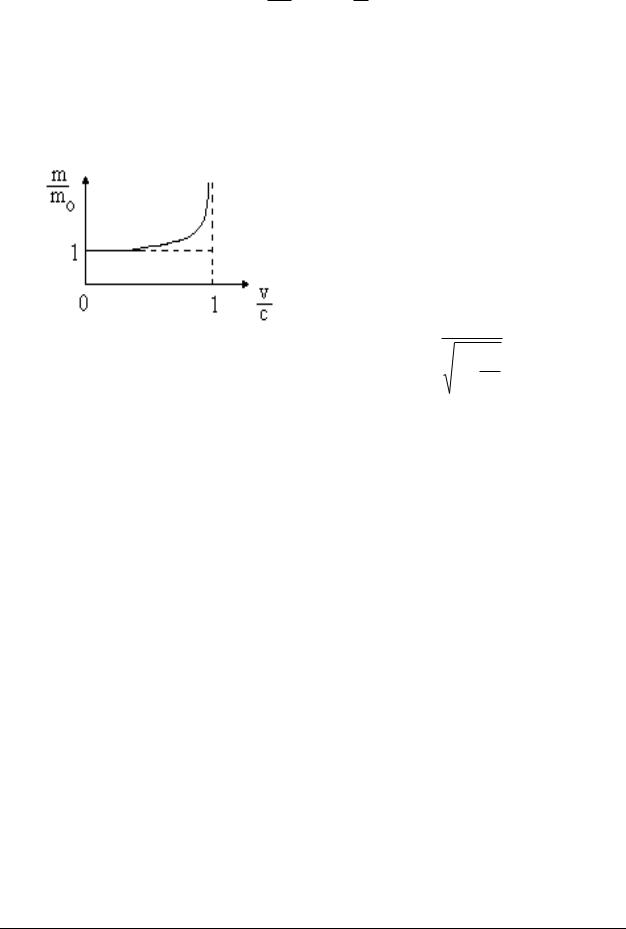
Опыт показал, что экспериментальная кривая отличается от параболы, особенно на участке, соответствующем большим скоростям. И это указывало на то, что масса электронов зависит от их скорости. Данная зависимость представлена на рис. 1.9, где m – это релятивистская масса, а mo – это масса покоя, т.е. масса тела при его скорости v,

стремящейся к нулю.

Формула для вычисления массы тела в зависимости от его скорости была впервые получена в 1904 г. Лоренцом:

Рис. 1.9

	m
m	o
			2
		v
	1
			2
		c

. (1.15)

Объяснение такой зависимости массы от скорости было дано теорией относительности, построенной в 1905 г. Эйнштейном. Согласно этой теории, данная зависимость является универсальным законом, не зависящим от свойств тел.

Физическую природу увеличения массы тела от скорости можно понять, если рассмотреть случай малых скоростей v << с. Разлагая дробь перед mo в выражении (1.15) в ряд Маклорена и ограничиваясь вторым слагаемым в разложении, получим

						mv2
		1 v 2
	m mo (1				) mo	2	.
		2 c 2				c 2

Второе слагаемое является добавкой к массе покоя и равно отношению кинетической энергии тела к квадрату скорости света, поэтому увеличение массы тела обусловлено увеличением его кинетической энергии.

б. Сила и импульс В классической механике (механике Ньютона) при v << с сила F опре-

деляется либо как первая производная импульса p по времени t, либо как произведение массы m на ускорение:

ГОУ ВПО УГТУ-УПИ 2005

Стр. 18 из 142

Кислов А.Н.									Атомная физика
			d
					m	dv	.
	F		dt	p		dt
				mv
Это уравнение инвариантно по отношению к преобразованиям Галилея.
В релятивистской механике при v ≈ с сила									определяется только как
								F
	по времени t:
производная импульса p

		d
F		dt

	d
p	dt	(mv)

.

Это уравнение инвариантно по отношению к преобразованиям Лоренца, которые переходят в преобразования Галилея при малых скоростях v << с. Дифференцируя импульс по времени и учитывая, что масса не является постоянной величиной, получим

					dm
			m	dv		.
		F		dt	v
					dt
Видно, что сила		равна сумме двух векторов, из которых один параллелен
	F

ускорению, другой – скорости. Из данного уравнения следует, что в реляти-

вистской механике, в отличие от классической механики, сила и ускорение в
общем случае не будут направлены одинаково. Сила			F	будет направлена так
же, как ускорение, в двух частных случаях:
1)	если сила F направлена перпендикулярно скорости			v ,
2)	если сила F направлена параллельно скорости	v .
	в. Взаимосвязь между массой и энергией, импульсом и энергией
	Элементарная работа dА, совершенная силой F			при перемещении	dr

тела, в релятивистской динамике определяется так же, как в динамике Ньютона, а именно как скалярное произведение силы и перемещения:

dA Fdr .

Если сила действует на свободное тело, то затраченная работа dА равна, согласно закону сохранения энергии, изменению кинетической энергии тела

dTкин:

			dA = dTкин .
		d
Учитывая, что F			(mv) , напишем
		dt

ГОУ ВПО УГТУ-УПИ 2005

Стр. 19 из 142

Кислов А.Н.	Атомная физика

dTкин

	d						2
		(mv)dr d (mv)v (dmv mdv)v v						dm mvdv
	dt

.

(1.16)

С другой стороны, из релятивистской зависимости массы от скорости (1.15) следует, что

2	c	2	2	2	2	v	2	.
m			mo c		m

Дифференцируя это выражение по абсолютной величине скорости v , получим равенство

c 2	2m	dm	0 v 2 2m	dm	m2	2v
		dv		dv

Умножив его на dv, приходим к выражению

.

c	2	dm v	2	dm mvdv

.

Сравнивая правые части этого выражения и выражения

что

dTкин c		2	dm .
Проинтегрировав данное равенство
T			m
dT кин c 2			dm ,
0			mo
получим
Tкин (m mo )c	2		mc	2	mo c	2	.

(1.16), видим,

(1.17)

Это есть релятивистское выражение для кинетической энергии тела. Первое слагаемое представляет собой релятивистскую полную энергию Е тела. Она может быть вычислена по формуле, называемой формулой Эйнштейна:

E mc2		mo c 2		.	(1.18)

1 v 2

c 2

ГОУ ВПО УГТУ-УПИ 2005

Стр. 20 из 142