Квантовая физика

Кислов А.Н.	Атомная физика

удовлетворять условиям: они являются однозначными, всюду конечными и непрерывными.

Условие нормировки Ψ-функции частицы, находящейся в бесконечном пространстве, записывается в виде равенства

			2
				dVc
		(r , t)

1

.

(5.1)

Интеграл представляет собой вероятность обнаружить частицу в каком-либо месте пространства, а это вероятность достоверного события, следовательно, он равен единице. Нормированная Ψ-функция определена с точностью до множителя, модуль которого равен единице, т.е. до множителя еiα, где α – любое действительное число.

Отметим важный момент. В классической физике работают с формула-

ми, связывающими численные значения fo физических величин f. В кванто-
вой механике используют формулы, связывающие операторы		, соответ-
	f

ствующие этим физическим величинам f и действующие в пространстве Ψ-
функций. Оператор				действует на Ψ-функцию, и получается другая Ψ/-
			f
функция:		f Ψ = Ψ/. Если Ψ-функция является собственной функцией опера-
тора f	, то для него справедливо уравнение на собственные функции и зна-
чения:	f	Ψ = foΨ. Собственное значение fo оператора f соответствует чис-

ленному значению физической величины f в состоянии, описываемом Ψ- функцией.

Запишем несколько операторов, широко используемых в квантовой ме-

ханике. Оператор Гамильтона	H :
		H i		t		;
оператор проекции импульса		на ось х:
	px
		px	i			;
					x
оператор импульса p :
			i			,
		p

где – оператор градиента («набла»);

ГОУ ВПО УГТУ-УПИ 2005

Стр. 81 из 142

Кислов А.Н. Атомная физика

оператор кинетической энергии			T	кин (нерелятивистский случай):
						2			2
					p
		T кин									,
					2m			2m
где	2	– оператор Лапласа.

Зная волновую Ψ-функцию, можно вычислить значение fo физической величины f в состоянии, описываемом этой Ψ-функцией. Причем, согласно принципу неопределенности, fo является неким средним значением <f>, которое в координатном представлении находится по формуле

f o f		*			,
			(r ) f (r )dVc
V
c

где звездочка «*» означает комплексное сопряжение.

(5.2)

5.2. Волновое уравнение Шредингера. Стационарное уравнение Шредингера

Основным уравнением квантовой механики является уравнение Шредингера. Его используют для определения Ψ-функций в любой момент времени t. Подобно тому, как уравнения движения Ньютона в классической механике или уравнения Максвелла в классической электродинамике не могут быть выведены теоретически из каких-либо соотношений, а представляют собой обобщение большого числа экспериментальных фактов, уравнение Шредингера в квантовой механике также нельзя строго вывести из известных ранее соотношений. Его следует рассматривать как исходное предположение, справедливость которого доказывается тем, что все вытекающие из него следствия точно согласуются с опытными фактами.

К уравнению Шредингера можно прийти путем следующих рассуждений, учитывая, что оно является уравнением нерелятивистским. Согласно

гипотезе де Бройля, свободно двигающейся частице соответствует плоская

гармоническая волна с частотой ω = Е/ħ и волновым вектором k p , по-

этому для этой частицы волновую Ψ-функцию можно записать в виде (комплексная форма)

		i
(r , t) A exp( i( t kr )) A exp(			(Et pr )) .

ГОУ ВПО УГТУ-УПИ 2005

Стр. 82 из 142

Кислов А.Н.	Атомная физика

Продифференцировав Ψ-функцию по времени t, получим равенство

		i
(r , t)
t			E (r , t)

,

которое приведем к виду

i
	t	(r , t) E (r , t)
H

.

Данная запись представляет собой уравнение

собственные значения оператора Гамильтона H Дважды продифференцировав Ψ-функцию

соотношение

	1			2
(r , t)			p		(r ,
		2

которое запишем в виде

на собственные

.

по координатам

t)

,

функции и

	, получим
r

		2		p	2
	2m		(r , t)	2m		(r , t)
	T

.

Это есть уравнение на собственные функции и собственные значения опера-

тора кинетической энергии T кин.

Из классической физики известно, что в нерелятивистском случае для

p

2

свободной частицы справедливо равенство

E

, т.е. полная энергия рав-

2m

на кинетической энергии частицы. Следовательно,

для операторов H

и T кин

выполняется равенство H

=T

кин.

Таким образом,

для свободной частицы

можно записать уравнение

2

i

(r , t)

(r , t) ,

(5.3)

t

2m

которое называется уравнением Шредингера для свободной частицы.

ГОУ ВПО УГТУ-УПИ 2005

Стр. 83 из 142

Кислов А.Н.	Атомная физика

Если частица двигается в силовом поле U(r,t), то ее полная энергия Е равна сумме кинетической энергии Ткин частицы и энергии U(r,t):

			Е = Ткин + U(r,t) .
Оператор Гамильтона		H	в этом случае равен сумме операторов кинетиче-
ской T	кин энергии и энергии силового поля U (r, t) :

H

=

T

кин +

U (r, t)

=

T

кин + U (r, t) ,

где учтено, что оператор функции координат равен самой функции. Следовательно, получаем следующее уравнение:

				2
i
	t	(r , t)	2m		(r , t) U (r, t) (r , t)

называемое уравнением Шредингера. Замечания по уравнению Шредингера.

1. Это уравнение позволяет найти волновую функцию

,

(r

(5.4)

,t) для любого

момента времени t, если известно ее значение в начальный момент времени to.

2.Несмотря на то что уравнение содержит только первую производную по времени t, из-за наличия мнимой единицы оно имеет периодические решения, поэтому уравнение Шредингера называют волновым уравнением.

3.Поскольку уравнение содержит первую производную по времени t и вторую производную по координатам, его решения будут комплексными (это отличает его от классического волнового уравнения, имеющего вторую производную по времени t, решениями которого являются действительные числа).

4.Уравнение является дифференциальным уравнением в частых производных. Такие уравнения чаще всего аналитически не решаются. В связи с этим в квантовой физике существует очень узкий круг задач, решаемых в аналитическом виде.

Еслиоператор Гамильтона H не зависит явно от времени t или, что

равносильно, энергия силового поля U(r) не зависит явно от времени t (потенциальное поле), то полная энергия Е является постоянной величиной, и это соответствует случаю стационарных состояний. Волновая функция (r ,t)

стационарного состояния представляется стоячей монохроматической волной

ГОУ ВПО УГТУ-УПИ 2005

Стр. 84 из 142

Кислов А.Н. Атомная физика

и записывается в виде произведения двух функций, из которых одна есть

функция только координат		, а другая – времени t:
	r

		i	Et)
(r , t) (r ) exp(

.

Из уравнения Шредингера (5.3) для свободной частицы, находящейся в стационарных состояниях, вытекает уравнение, позволяющее найти решения

		:
(r ) , зависящие только от координат	r

	2m
(r )		2	E (r ) 0

,

(5.5)

которое называется стационарным уравнением Шредингера свободной частицы.

Для стационарных состояний с учетом наличия силовых полей имеем уравнение

	2m
(r )		2	(E U (r)) (r ) 0

называемое стационарным уравнением Шредингера.

,

(5.6)

5.3.Применение квантовой механики к простейшим задачам

остационарных состояниях частицы

Рассмотрим простые системы, для которых можно строго решить стационарное уравнение Шредингера (5.6). Хотя такие системы являются идеализацией физических систем, встречающихся в природе, во-первых, их исследование позволяет более полно понять методы квантовой механики, вовторых, полученные результаты в некотором приближении отражают свойства реальных систем.

Точные аналитические решения стационарного уравнения Шредингера могут быть получены для систем, в которых потенциальная энергия U(r) имеет определенный вид, например:

а) имеет постоянное значение во всем пространстве, б) имеет различные постоянные значения в отдельных областях про-

странства, переходя скачком от одного значения к другому на поверхностях, разделяющих такие области. Причем на этих поверхностях на волновую Ψ-функцию накладываются следующие граничные условия: 1) она должна

ГОУ ВПО УГТУ-УПИ 2005

Стр. 85 из 142

Кислов А.Н.	Атомная физика

быть непрерывной, 2) если скачок потенциальной энергии U(r) конечный, то и grad Ψ тоже должен быть непрерывный.

Рассмотрим два простых примера, которые допускают точное решение стационарного уравнения Шредингера.

Пример 1. Исследуем поведение частицы с массой m в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Предположим, что частица двигается вдоль координатной оси х. Ее движение ограничено двумя непроницаемыми стенками с координатами

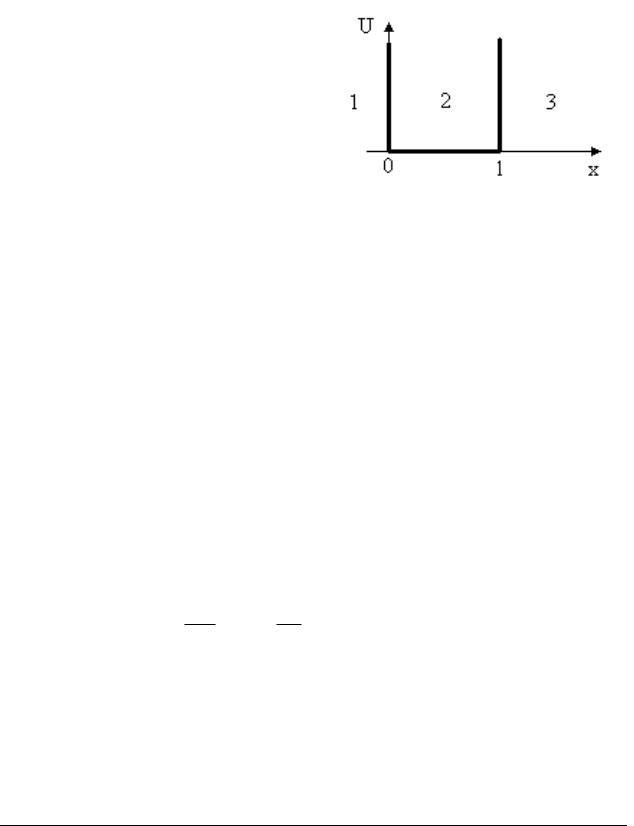
х = 0 и х = l. Потенциальная энергия U(х) частицы должна удовлетворять требованиям:

	,	ïðè	õ 0 è x l	,
U (x)
	0,	ïðè	0 x l .

Рис. 5.1

График потенциальной энергии U(х) приведен на рис. 5.1. Назовем область с х ≤ 0 областью 1, область 0 < х < l областью 2 (потенциальной ямой), а область с х ≥ l областью 3.

Рассмотрим вначале, как ведет себя в такой яме классическая частица. В области 2 частица двигается с кинетической энергией Ткин, равной полной энергии Е. При этом полная энергия Е частицы может иметь любое значение от 0 до ∞. Подойдя к области 1 или 3, частица отразится от стенки и будет двигаться в противоположную сторону. Таким образом, частица не может находиться вне потенциальной ямы, а может с равной вероятностью находиться в любом месте потенциальной ямы с произвольным значением полной энергии Е.

Частица, подчиняющаяся законам квантовой механики, ведет себя иначе. Для того чтобы показать это, необходимо решить стационарное уравнение Шредингера:

d	2
dx		2

	(x)	2m		(E U (x)) (x) 0
			2

.

За пределы потенциальной ямы, т.е. в областях 1 и 3, частица попасть не может, поэтому вероятность ее обнаружения, а следовательно, и ее волновая Ψ-функция в этих областях равны нулю. Из условия непрерывности

ГОУ ВПО УГТУ-УПИ 2005

Стр. 86 из 142

Кислов А.Н.	Атомная физика

Ψ-функции следует, что она должна равняться нулю на границе потенциальной ямы, т.е. получаются следующие граничные условия:

(0) 0 и (l) 0 .

(5.7)

В области 2 Ψ-функция не равна нулю, а стационарное уравнение Шредингера принимает вид однородного дифференциального уравнения второго порядка с постоянными коэффициентами:

где

k	2

2m
	2

d	2		2
				(x) 0
		2	(x) k
dx

E .

,

Решения данного уравнения можно записать в виде

(x) Asin kx B cos kx

.

Используя граничные условия (5.7), найдем вид Ψ-функции, удовлетворяющей им. Из условия для х = 0: (0) A sin 0 B cos 0 0 – следует, что

для выполнения этого вен нулю, поэтому (

равенства необходимо, чтобы x) A sin kx . Из условия для х

коэффициент В

= l: (l) A sin

был

kl

ра-

0 –

следует, что это равенство выполняется, когда

	ство справедливо при	kl n	или	k	n	, где
					l

sin kl 0

. Последнее равен-

n = 1, 2,…. Следовательно,

волновая Ψ-функция , характеризующая n-е стационарное состояние частицы в области 2, имеет вид

n (x) Asin nl x .

Значение коэффициента А находится из условия нормировки Ψ-функции

(5.1):

		2	l	2	n x
	A		sin			dx 1 .
					l
			0

ГОУ ВПО УГТУ-УПИ 2005

Стр. 87 из 142

Кислов А.Н.	Атомная физика

Понизим степень подынтегрального выражения и вычислим интеграл

	l	2	n x	l	1	cos(2n x / l)
	sin			dx			dx 1/ 2
			l			2
	0			0

.

	В результате находим	A	2	.
			l

Окончательно получаем

	(x)	2	sin	n	x
n		l		l

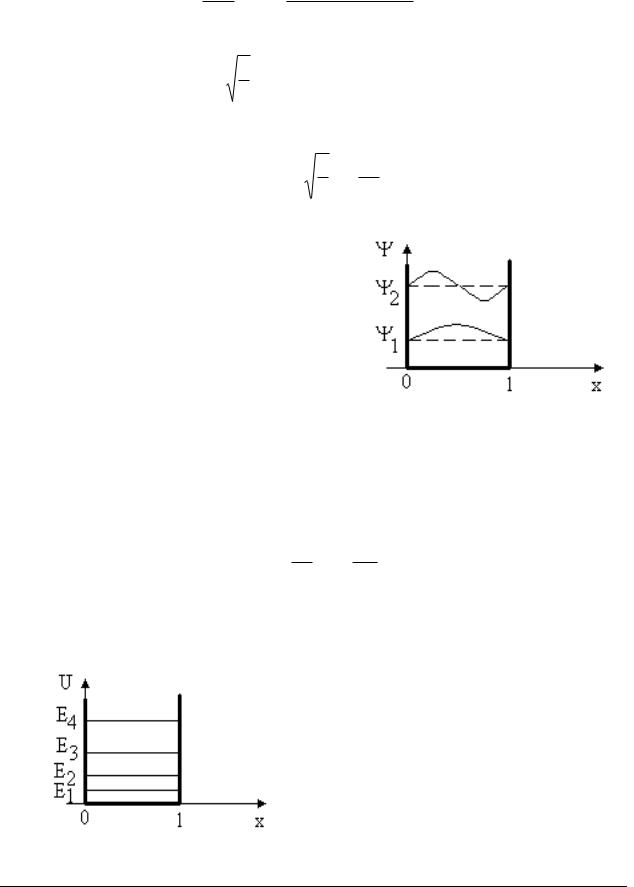
На рис. 5.2 приведены графики собственных Ψ-функций для состояний с n = 1 и n = 2.

.

(5.8)

Рис. 5.2

Для нахождения собственных значений энергии E стационарных состояний воспользуемся равенством

откуда следует, что

Рис. 5.3

k	2

	n		2	2m
						E ,
					2
	l

E E			2		2	n2 .	(5.9)
	n				2
			2ml

Таким образом, граничным условиям удовлетворяют значения энергии Е только из дискретного ряда En, а это означает, что частица в потенциальной яме может иметь только квантованные значения полной энергии En, зависящие

ГОУ ВПО УГТУ-УПИ 2005

Стр. 88 из 142

Рис. 5.5

Кислов А.Н. Атомная физика

	от n-го состояния частицы (рис. 5.3). Причем расстояние		Еn между сосед-
	ними энергетическими уровнями с ростом n будет возрастать:
			2		2
	En En 1 En					(2n 1) .
		2ml			2

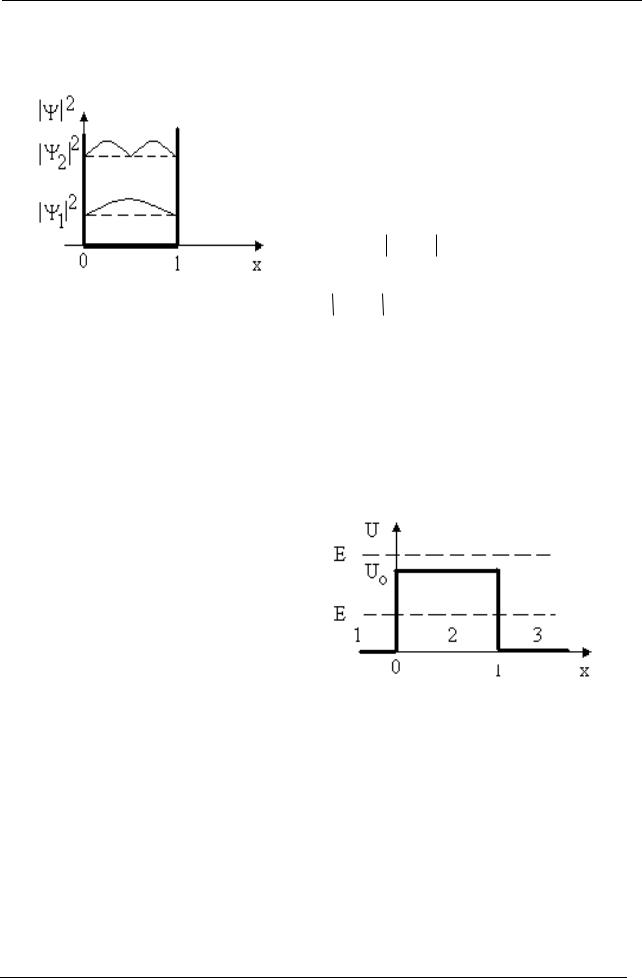
Вероятность обнаружения частицы, находящейся в n-м состоянии в потенциальной яме, характеризует квадрат

Рис. 5.4

модуля	n (x)		2	волновой функции
n (x) . На рис. 5.4 представлены графи-
ки n (x)	2	для состояний с n = 1 и n = 2.

Из них видно, что вероятность обнаружения частицы в потенциальной яме зависит от ее состояния и места ее обнаружения в яме.

Пример 2. Рассмотрим прохождение частицы с массой m и полной энергией Е через одномерный прямоугольной потенциальный барьер. Допустим, что координатная ось х сонаправлена с направлением движения частицы. Частица движется в силовом поле, потенциальная функция которого изображена на рис. 5.5. Потенциальная энергия U(х) частицы в этом случае удовлетворяет требованиям:

	0,			ïðè	õ 0 è x l	,
U (x)
	U	o	,	ïðè	0 x l .

Назовем область с х ≤ 0 областью 1, область 0 < х < l областью 2 (прямоугольным потенциальным барьером высоты Uo), а область с х ≥ l областью 3.

Рассмотрим, как ведет себя классическая частица при прохождении этого потенциального барьера. Если полная энергия Е частицы меньше значения Uo (Е < Uo), то частица отразится от потенциального барьера и останется в области 1. Если Е > Uo, то частица свободно преодолеет потенциальный барьер и перейдет в область 3.

Квантовая частица ведет себя совершенно иначе. Всегда имеется некоторая вероятность, что при Е < Uo частица пройдет через потенциальный барьер (это явление называется «туннельный» эффект) и окажется в области 3, а при Е > Uo частица отразится от барьера и обнаружится в области 1.

Для характеристики этих вероятностей вводятся такие величины, как коэффициент прозрачности D и коэффициент отражения Rотр потенциально-

ГОУ ВПО УГТУ-УПИ 2005

Стр. 89 из 142

Кислов А.Н.	Атомная физика

го барьера. Коэффициент прозрачности D равен вероятности прохождения частицы сквозь потенциальный барьер и определяется как отношение интенсивности Iпр, прошедшей сквозь барьер, к интенсивности Iпад, падающей на барьер волны де Бройля:

D = Iпр / Iпад .

Коэффициент отражения Rотр – это вероятность того, что частица испытает отражение от потенциального барьера, он равен отношению интенсивности Iотр, отраженной от барьера, к интенсивности Iпад, падающей на барьер волны де Бройля:

Rотр = Iотр / Iпад.

Причем выполняется такое равенство:

D + Rотр = 1 ,

так как сумма D и Rотр дает вероятность достоверного события: частица либо пройдет через барьер, либо отразится от барьера.

Для того чтобы найти коэффициенты D и Rотр, нужно решить стационарное уравнение Шредингера:

d	2
dx		2

	(x)	2m		(E U (x)) (x) 0
			2

.

Учитывая, что потенциальная энергия U(х) является разрывной функцией, необходимо решить данное стационарное уравнение Шредингера для каждой области 1, 2 и 3, т.е. найти волновые функции Ψ1, Ψ2 и Ψ3, описывающие состояние частицы в этих областях.

Из условия непрерывности Ψ-функции и ее первой производной Ψ/ по координате х на границах областей, где происходит конечный скачок функции U(х), получаются следующие граничные условия:

(0)				(0)		,
	1		2
	/			/	(0)
		(0)
	1			2

и

		(l) 3(l) ,
	2
	/	/	(l) .
		(l)
	2	3

(5.10)

Считая, что Е > Uo, напишем стационарное уравнение Шредингера для области 1:

ГОУ ВПО УГТУ-УПИ 2005

Стр. 90 из 142