4.4. Аттракторы

Границы области движения частицы и вид траектории существенно зависят от начальных условий. Выбирая разные начальные условия, мы можем получить целый пучок траекторий. Эти траектории похожи на линии тока в жидкости, что дало основание иногда называть их «линиями тока», а их совокупность - «потоками».

Выше мы показали, что в наших примерах траектории на плоскости не обязательно приходят из бесконечности и заканчиваются на бесконечности; они могут по-разному заканчиваться при конечных значениях координат. Эти свойства являются достаточно общими. Точки, в которых траектории заканчиваются, являются как бы точками притяжения для линий тока; сами конечные точки называются аттракторами. На плоскости траектории могут не только заканчиваться в точках (как на рис. 14.4,а), но и навиваться на так называемый предельный цикл (см. рис. 13.4). Предельный цикл будет устойчивым, если к нему притягиваются соседние траектории. Он также принадлежит к классу аттракторов.

Рис. 14.4

Аттракторы - точки на плоскости - бывают двух типов: узлы и фокусы; они отличаются видом зависимости координат от времени. На рис. 14.4,а изображены траектории, заканчивающиеся в (устойчивом) узле. Если обратить время, т. е. заменить на , то траектории будут выходить из узла. Такой узел будет уже неустойчивым. На рис. 14.4,б приведена временная зависимость координаты в случае узла.

Понятия узла, фокуса и предельного цикла, как видно, здесь не геометрические. Они скорее определяют тип расположения траекторий автономной системы дифференциальных уравнений 1-го порядка:

.

Автономной называют систему уравнений, в которой функции и явно от времени не зависят.

На рис. 15.4,а изображены траектории, заканчивающиеся в (устойчивом) фокусе. Они примыкают к точке , наматываясь на нее подобно логарифмическим спиралям. В случае узла траектории подходят как бы по нормали к окружности радиуса с центром в узле. При замене на траектории, изображенные на рис. 15.4,а будут выходить из фокуса, который станет неустойчивым. На рис. 15.4,б дана зависимость координат от времени в случае фокуса. Заметим, что не обязательно декартовы координаты.

Рис. 15.4

Следует иметь в виду, что классификацию особых точек (линий) проводят на основе системы уравнений 1-го порядка по времени. Можно дать достаточно строгое математическое определение устойчивого многообразия (особой точки). Под устойчивым многообразием (особой точки) понимается множество всех точек, которые являются начальными точками траекторий, заканчивающихся при в данной особой точке. Под неустойчивым многообразием (особой точки) понимается множество начальных траекторий, заканчивающихся в пределе в данной особой точке.

4.5. Задача кеплера

Траектория частицы независимо от начальных условий является замкнутой при движении частицы в поле

. (19.4)

Рассмотрим задачу о движении частицы массыт в этом поле, не ограничиваясь случаем . Если , то сила , с которой поле действует на частицу, является силой притяжения (она направлена по радиусу-вектору центру поля), если , то на частицу действует сила отталкивания. Эффективная энергия частицы в том и другом случае изображена на рис. 16.4.

Из анализа графика следует, что движение частицы в поле притяжения будет инфинитным, если (в области ), и финитным, если (в области ). При частица будет двигаться по окружности. В поле отталкивания полная энергия частицы всегда положительна, а движение инфинитно.

Рис. 16.4

Траектория частицы, ее орбита определяется интегралом.

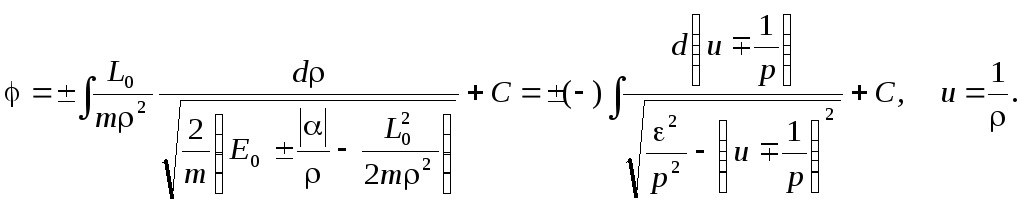
Здесь верхние знаки в подынтегральном выражении соответствуют случаю , а нижние - случаю , введены следующие обозначения: - параметр, - эксцентриситет орбиты. Вычисляя интеграл, получим

. (20.4)

Опуская знак перед функцией справа ввиду четности косинуса и обращая формулу, найдем уравнение орбиты в явном виде:

. (21.4)

Удобно полярную ось направить на ближайшую к центру силы точку траектории. Тогда . Уравнением (21.4) описывается кривая второго порядка, в фокусе которой находится начало координат². Из аналитической геометрии известно, что в зависимости от величины траектории вида (21.4) представляют собой гиперболу (при ), параболу (при ), эллипс () или окружность (). Учитывая зависимость от полной механической энергии частицы, получим, что в потенциальном поле , траекторией частицы будет гипербола, если - парабола, если - эллипс, если - окружность, если ; в случае отталкивания траекторией частицы всегда будет гипербола, так как в этом случае (а ) всегда.

Рассмотрим финитное движение частицы в поле , когда орбита является эллипсом. По известным формулам аналитической геометрии можно найти большую и малую полуоси эллипса в виде

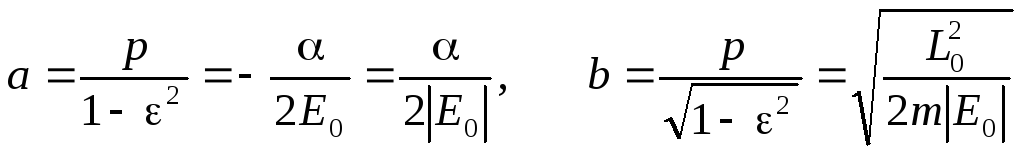
Отсюда видно, что большая полуось эллипса зависит только от энергии (но не от момента импульса) частицы. В квантовой механике именно это свойство приводит к правилу квантования по Бору.

Наименьшее и наибольшее расстояния до центра поля (фокуса эллипса) равны

(22.4)

Заметим, что эти значения можно получить и как корни уравнения .

Период движения определим с помощью закона сохранения момента импульса, записанного в форме

, (23.4)

где площадь, очерчиваемая радиус-вектором частицы за время Интегрируя это равенство по времени от нуля до , получим

. (24.4)

Здесь мы учли, что , так как орбитой является эллипс. Отсюда находим

, (25.4)

т. е. квадрат периода обращения пропорционален кубу линейных размеров орбиты (третий закон Кеплера) и зависит только от полной энергии частицы.

При движение инфинитно. В поле притяжения при траектория является гиперболой, огибающей центр поля (фокус). Наименьшее расстояние, на которое частица подходит к центру поля, равно

,

где - полуось гиперболы.

В случае частица движется по параболе, при этом наименьшее расстояние . Этот случай осуществляется если при частица покоится.

В поле отталкивания траектория, как уже говорилось выше, является гиперболой (см. рис. 16.4). Наименьшее расстояние от орбиты до центра поля в этом случае равно

,

где полуось гиперболы.