§6. Частная спектральная задача

Частная спектральная задача – задача нахождения некоторых собственных чисел матрицы и соответствующих собственных векторов.

1.Вариационный метод

Пусть А – симметричная матрица. Найдем её максимальное собственное число. Т.к. из ранее доказанного , то задача сводится к нахождению стационарных точек функционала.

2.Степенной метод

Для матрицы А предположим, что:

а) её собственные вектора φ₁… φ_nобразуют базис вRⁿ.

б) её собственные числа удовлетворяют неравенствам | λ₁ |>| λ_k|,k=2..n.

Тогда всякий вектор х из Rⁿможет быть представим в виде:.

Построим последовательность векторов:

x⁽¹⁾=Ax,x⁽²⁾=Ax⁽¹⁾…x^(m)=Ax^(m-1)=A^mx.

Значит, . Преобразуем правую часть равенства:

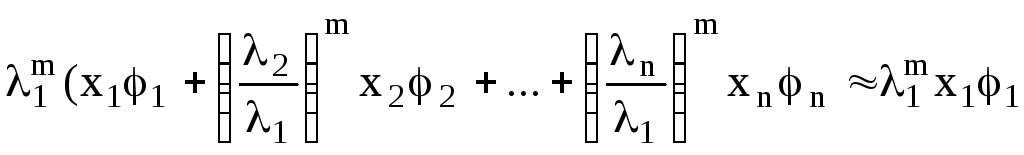приm>>1,

т.к. тогда .

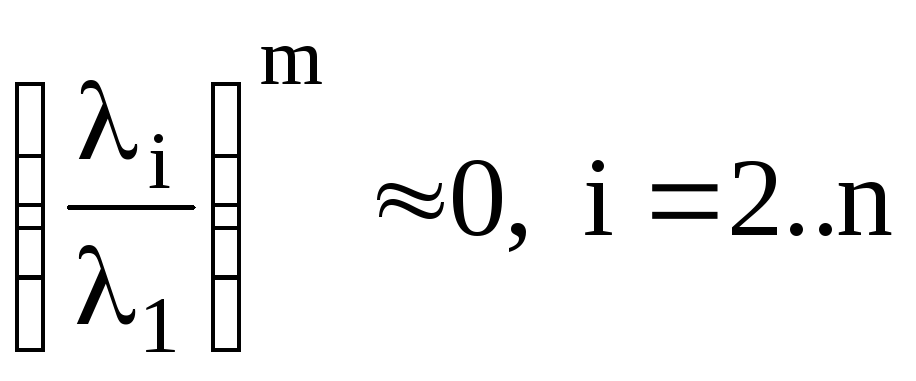Получим, что:

,

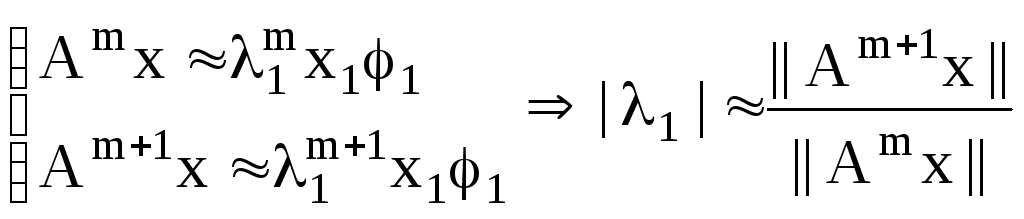а - соответствующий собственный вектор

(т.к. он определяется с точностью до скалярного множителя).

Знак λ₁найдем из следующего равенства:

- знак находится по первой компоненте.

Точность метода: .

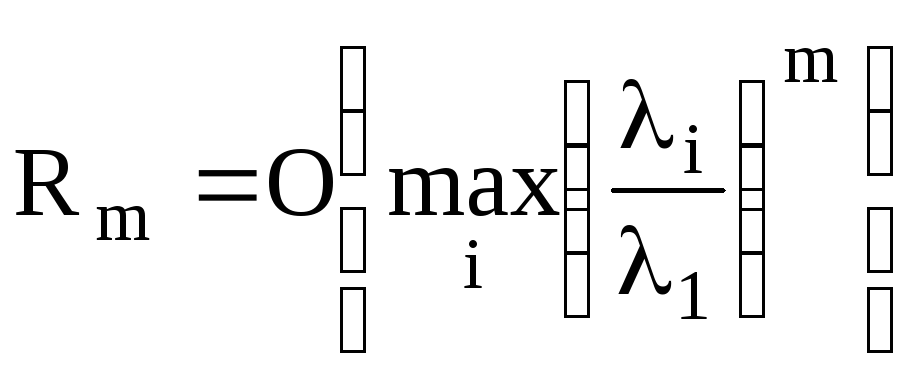§7. Метод максимизации столбцов

Пусть A=(a_kp) – вещственная, квадратная матрица порядкаn.

Обозначим как a_p–pый столбец матрицы.

Заметим, что ; .

Рассмотрим матрицу простого поворота U_p:

u₁₁=u_pp=c=cosα, -u_p1 =u_1p= -s= -sinα, остальные диагональные элементы равны 1, а недиагональные – нулю. Из ранее доказанного матрицаU_pосуществляет поворот на угол α против часовой стрелки.

1.Максимизация первого столбца

Рассмотрим матрицу B=AU_p=(b_ij).

В ней: b₁=ca₁+sa_p,b_p= -sa₁+ca_p. Остальные столбцы совпадают со столбцами А.

Свойство 1

Доказательство

Действительно:

.

Отсюда .

Что и требовалось доказать.

Выберем угол α в матрице U_pтак, чтобы |b₁| был максимален.

Рассмотрим функцию

Тогда .

Обозначим α=α_p:f’(α)=0. Будем выбирать α_pпо правилу:

а) если, то

б) иначе α_pнаходится из равенства

в)заметим, что α_p=0 тогда и только тогда, когда.

Свойство 2 Если |a₁|≥|a_p|, то |b₁|≥|a₁|≥|a_p|≥|b_p| и |b₁|>|a₁| при.

Доказательство

Действительно:

1)Пусть. Тогдаи.

Следовательно, из определения f(α): .

Отсюда:

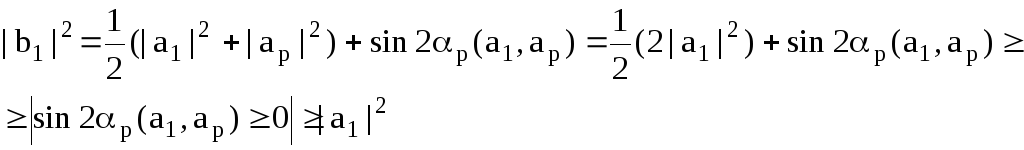
и | b₁|>|a₁| при.

2)Пусть.

Рассмотрим функцию .

Т.к. ,,a, то

f’’(α_p)≤0, т.е.α_p– локальный максимум () и общий максимум функции на.

Следовательно, .

Что и требовалось доказать.

Свойство 3Если |a₁|≥|a_p|, то, т.е. новые столбцы ортогональны.

Доказательство

Действительно:

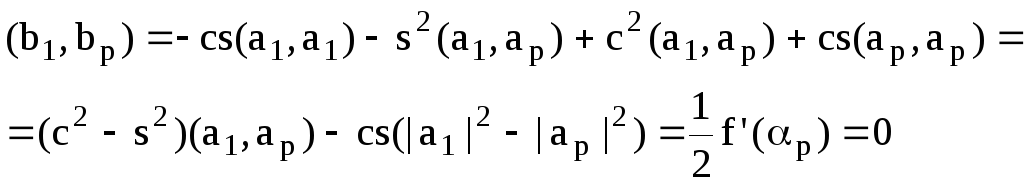
Что и требовалось доказать.

2.Алгоритм сингулярного разложения

Пусть дана матрица A=(a_ij). Рассмотрим матрицуA₁=AU₁, гдеU₁– ортогональная матрица перестановки столбцов: первый столбец матрицы А₁максимален.

Рассмотрим последовательность матриц: A_k+1=A_kU_p(k),k=1,2…,

где p(k) – номер столбца (= 2,3..n; 2,3..);

U_p(k)– матрица простейшего поворота:

u₁₁ = u_p(k)p(k)= c =cosα, -u_p(k)1 = u_1p(k)= -s = - sinα,

остальные диагональные элементы равны 1,

а недиагональные – нулю.

Т.е. у всех A_kпервый столбец максимальный, у всехA_k+1первый столбец ортогоналенp(k+1). При этом сумма квадратов сохраняется.

Обозначим . Действительно, тогда.

Отсюда следует лемма:

Лемма 1Последовательность нормпервых столбцов матриц сходится.

Доказательство

По Свойству 2 предыдущего пункта последовательность не убывает.

А из сохранения суммы квадратов она ограничена, а значит сходится.

Замечание Отсюда не следует сходимость векторов.

Лемма 2 Последовательность матриц {A_k} сходится поэлементно приk→∞ (без доказательства).

Т.е. . Эта матрица обладает следующими свойствами:

1)первый столбец наибольший по модулю

2)первый столбец ортогонален всем остальным.

Действительно, предположим противное . Умножим наU_p1, получим требуемое.

Таким образом, получен алгоритм сингулярного разложения.

Пусть матрица А nого порядка. Построим последовательностьA_k→A_∞.

1.Обозначим какв процессе максимализации первого столбца. Т.о. первый столбец макимален и ортогонален всем остальлным.

2.Максимизируем второй столбец матрицы с помощью последующих, не изменяя первый. Полученная последовательность матриц сходится к некоторой матрице.

3.И т.д.

n-1.Максимизируем (n-1)ый столбец у матрицы. Получим матрицус монотонными нормами и взаимоортогональными столбцами.

Запишем полученную матрицу в виде: , где ортогональная матрицаVесть произведение ортогональных матриц.

Обозначим нормы столбцов матрицы какS_k.

Получим 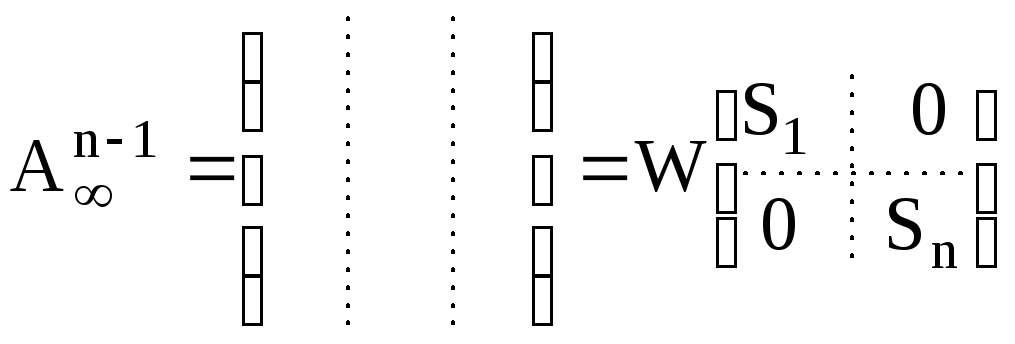, гдеW– ортогональная матрица.

Таким образом, AV=WS, т.е.A=WSV^T–SVD-разложение.