
- •Глава1. Проблема аппроксимации
- •§1. Полиномиальная апппроксимация
- •§2. Интерполяционный полином в форме Лагранжа
- •§3. Интерполяционный полином в форме Ньютона
- •§4. Аппроксимация сплайнами
- •§5. Метод наименьших квадратов
- •§6. Полиномиальная интерполяция с кратными узлами
- •§7. Свойства разделенных разностей
- •§8. Задача Чебышева. Разрешимость системы
- •§9. Теорема Чебышева
- •§10. Многочлены Чебышева
- •Глава2. Численное дифференцирование
- •Глава3. Численное интегрирование
- •§1. Интерполяционные квадратурные формулы
- •1.Интерполяционные квадратурные формулы
- •2.Интерполяционные квадратурные формулы наилучшей алгебраической точности
- •3.Ортогональные многочлены и их свойства
- •§2. Применение квадратурных формул
- •§3. Метод Монте-Карло (метод статистических испытаний)
- •§4. Правило Рунге практической оценки погрешности
- •Глава4. Алгебраическая проблема собсвенных значений
- •§1. Ортогональные матрицы
- •1.Ортогональные матрицы
- •2.Матрица элементарного поворота
- •§2. Вариационное свойство собственных значений
- •§3. Приведение симметричной матрицы к диагональному виду
- •§4. Сингулярное разложение матрицы
- •§5. Сопряженная матрица
- •§6. Частная спектральная задача
- •1.Вариационный метод
- •2.Степенной метод
- •§7. Метод максимизации столбцов
- •1.Максимизация первого столбца
- •2.Алгоритм сингулярного разложения
- •3.Главное собственное число
- •§8. Метод вращения
§9. Теорема Чебышева
Решение задачи Чебышева:
Определить:
![]()
минимизирующий многочлен Pn(x,A), если он существует.
Теорема: Такой многочлен сущестует и совпадает с решением системы
![]() т.е. Pn(x,A)=Pn(x,A*).
т.е. Pn(x,A)=Pn(x,A*).
Доказательство
Не ограничивая общности будем считать,
что
![]()
Если это не так, рассмотрим функцию -f(х) в системе все уравнения умножим на (-1), тогда решением будет многочлен –Pn(x,A*).
Перепишем систему следующим образом:
![]() .
.
Воспользуемся свойствами чисел αk:
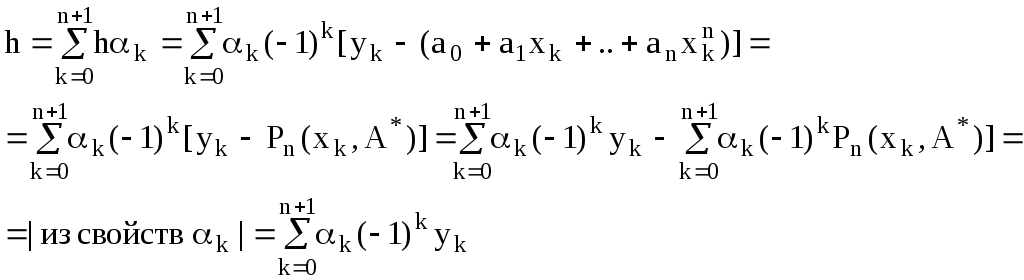
При этом:
![]() .
.
Однако μ>h, т.к. иначе получимh<h. Значит, μ=h. И для всякогоkмаксимум разницы междуPn(x) иf(x) не может быть меньше.
Далее нетрудно доказать, что многочлены Pn(x,A*) иPn(x,A0) равны.
Что и требовалось доказать.
Замечание Можно рассмотреть
континуальный аналог задачи Чебышева.
Необходимо найти для![]() и минимизирующий многочленPn(x,A0),
если он существует.
и минимизирующий многочленPn(x,A0),
если он существует.
Этот многочлен есть решение дискретной задачи при некотором наборе узлов.
§10. Многочлены Чебышева
Постановка задачи:
Для многочленов Pn(x,A)
степениncoстаршим коэффициентом, равным 1, требуется
определить для![]() и минимизирующий многочленPn(x,Amin),
если это возможно.
и минимизирующий многочленPn(x,Amin),
если это возможно.
Таким образом, рассматривается задача о многочленах со старшим коэффициентом, равным 1, наименее отклоняющихся от нуля.
Рассмотрим многочлены Чебышева:
![]()
ТеоремаTn(x) – многочлены степениnсо старшим коэффициентом, равным 1, методом математической индукции.
Доказательство
При n=1:
![]() -
многочлен 1ой степени.
-
многочлен 1ой степени.
При n=2:
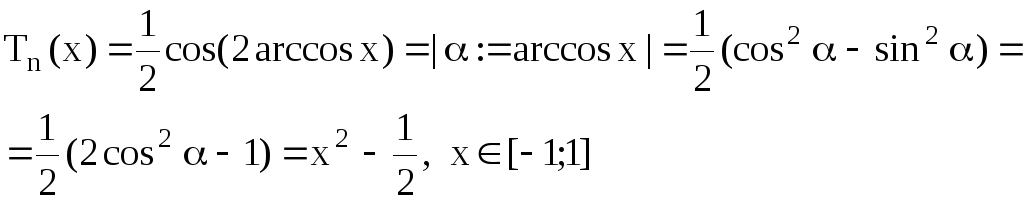
Пусть утверждение верно
![]() .
Докажем дляn=k.
.
Докажем дляn=k.
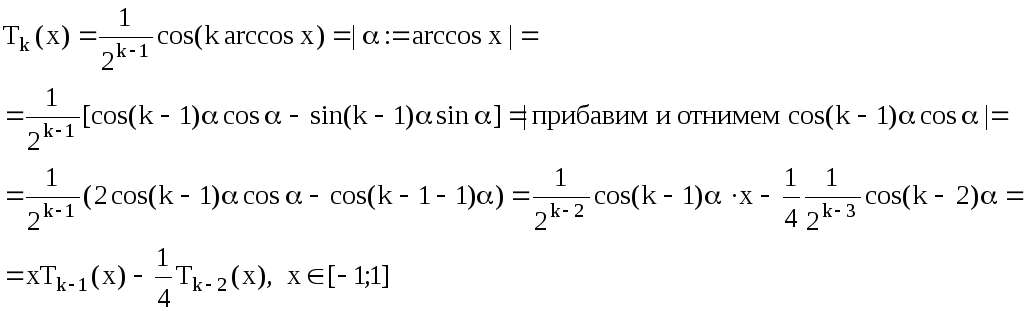 Заметим,
чтоTk-1(x)
– многочлен степениk-1
по предположению,Tk-2(x)
– многочлен степени (k-2).
Таким образом,Tk(x)
– многочлен степениkсо
старшим коэффициентом, равным 1.
Заметим,
чтоTk-1(x)
– многочлен степениk-1
по предположению,Tk-2(x)
– многочлен степени (k-2).
Таким образом,Tk(x)
– многочлен степениkсо
старшим коэффициентом, равным 1.
Что и требовалось доказать.
Теорема (свойство четности) Все многочленыT2n(x) являются четными функциями, аT2n+1(x) – нечетными.
Доказательство
При n= 0:T0=1 – четная функция;T1=x– нечетная.
Пусть утверждение верно
![]() .
Докажем его справедливость дляn=k.
.
Докажем его справедливость дляn=k.
Заметим, что из предположения T2k-1– нечетная функция,T2k-2– четная.
Тогда
![]() -
четная функция,
-
четная функция,
а![]() -
нечетная.
-
нечетная.
Что и требовалось доказать.
Нули многочленов Чебышева
Заметим, что:
![]() .
.
Обозначим
![]() .
.
Тогда
![]() .
.
Т.к.
![]() .
.
![]() -
нули многочлена ЧебышеваTn(x)
на [-1;1].
-
нули многочлена ЧебышеваTn(x)
на [-1;1].
П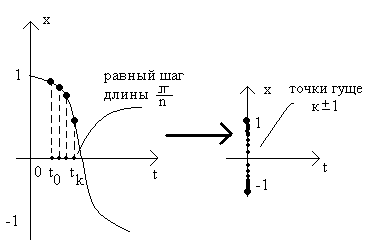 ри
этом других нулей нет (т.к. многочленnой степени имеет не болееnнулей).
ри
этом других нулей нет (т.к. многочленnой степени имеет не болееnнулей).
Экстремумы.
Рассмотрим локальные экстремумы Тn(x) на [-1;1].
Т.к.
![]() то точками экстремума для Тn(х)
на [-1;1] будут точки, где
то точками экстремума для Тn(х)
на [-1;1] будут точки, где![]()
Следовательно, cos(n·arccosx) = ±1
n·arccosx=πk,
![]()
![]()
Обозначим
![]() где
где![]()
Отсюда,
![]() .
.
Т.к.
![]() .
.
![]()
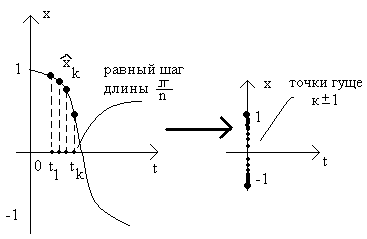 -
экстреальные точки дляTn(x)
на [-1;1].
-
экстреальные точки дляTn(x)
на [-1;1].
Ортогональность с весом
![]()
Функции f(x)
иg(x)
ортогональны на [a;b]
с весом ρ(x), если![]() (ортогональность в смысле Гильбертова
пространстваL2[a;b]).
(ортогональность в смысле Гильбертова
пространстваL2[a;b]).
Доказательство
Обозначим
![]()
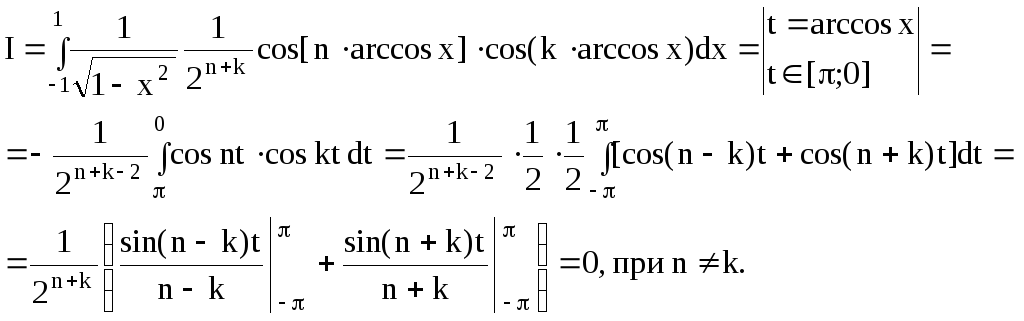
Что и требовалось доказать.
Лемма
Tn(x) – многочлены со старшим коэффициентом равным еденице, наименее отклоняющиеся от нуля на [-1;1]. Т.е. еслиPn(x) – многочлен степениnсо старшим коэффициентом равным единице, то:
![]()
Доказательство
Предположим противное:
![]() .
.
Обозначим как Qn(x) =Tn(x)-Pn(x).
Заметим, что многочлен Qn(x):
1)имеет (n-1) степень
2![]() )
)![]() ,
т.к. из предположения .
,
т.к. из предположения .
Таким образом, получено, что между
каждыми двумя точками
![]() многочленQn(x)
меняет свой знак. Т.е. многочленQn(x),
отличный от нуля (т.к. он ≠0 в точках
многочленQn(x)
меняет свой знак. Т.е. многочленQn(x),
отличный от нуля (т.к. он ≠0 в точках![]() )
имеетnнулей, а значитQn(x)≡0.
)
имеетnнулей, а значитQn(x)≡0.
Противоречие доказывает требуемое.
