§1. Ортогональные матрицы

1.Ортогональные матрицы

Рассмотрим два ортонормированных базиса в пространстве Rⁿ: . Т.е..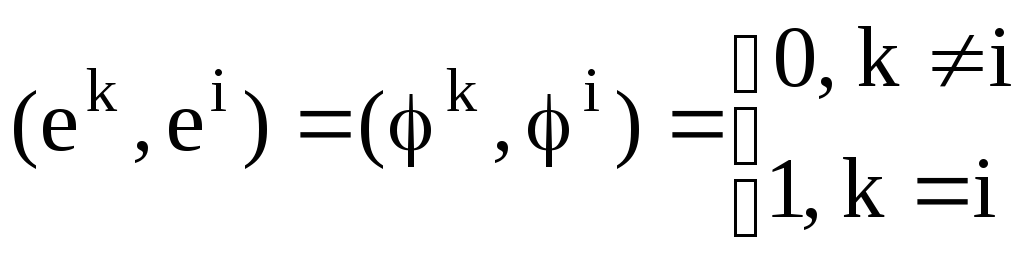

Разложим вектора второго базиса по векторам первого:

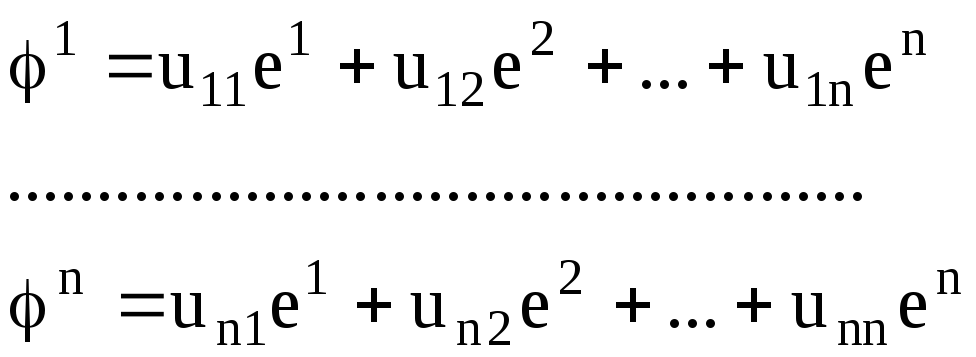
Обозначим как U=(u_ik).

Рассмотрим скалярное произведение:

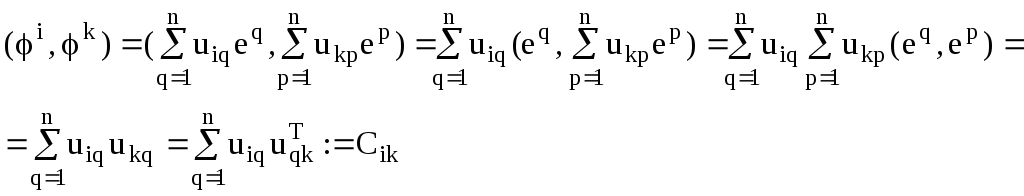
Таким образом, сумма C_ikтрактуется как произведениеiой строки матрицыUнаkый столбец матрицыU^T.Cдругой стороны, из свойств ортонормированного базиса матрицаC=(c_ik)=E.

Отсюда получим: UU^T=EилиU^TU=E.

Из выведенных формул следуют равенства:

1)U^-1 =U^T(из определения обратной матрицы)

2) (Ux,Uy) = (x,y) для любых векторовx,yизRⁿ(т.е. скалярные произведения векторов и их образов относительноUсовпадают).

Действительно, (Ux,Uy) = (UU^Tx,y) = (x,y)

3)Отсюда в частности следует: ||x|| = ||Ux||

Действительно, .

Матрица V, удовлетворяющая любому из этих трех равенств,ортогональная. Она обладает следующими свойствами:

1)переводит ортогональный базис в ортонормиррованный

2)сохраняет углы между векторами, а также их нормы

Представление матрицы-оператора в другом базисе

Из теорем линейных операторов:

1)Всякой матрице А можно сопоставить некоторый линейный оператор

Ω: x→y=Ax

2)Всякий линейный ограниченный оператор вRⁿпредставим в виде матрицы.

Рассмотрим некоторый ортонормированный базис и найдем представление в нем матрицы А.

Пусть x=(x₁..x_n)^Tв базисе .

Т.е. .

Рассмотрим оператор Ω: x→yв . Т.е. оператор(β – оператор Ω в новом базисе).

- представление матрицы А в базисе .

2.Матрица элементарного поворота

Рассмотрим матрицу элементарного поворота в двух пространствах:

1)в пространствеR²:

Рассмотрим матрицу, где с=cosα,s=sinα.

Тогда .

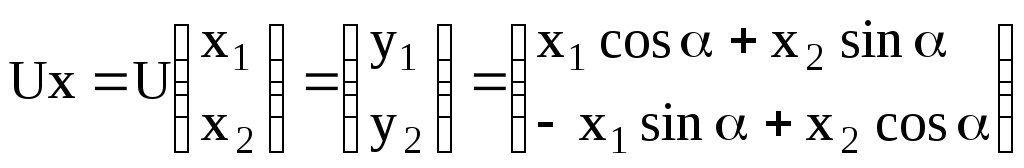Докажем, что U– ортогональная матрица:

;

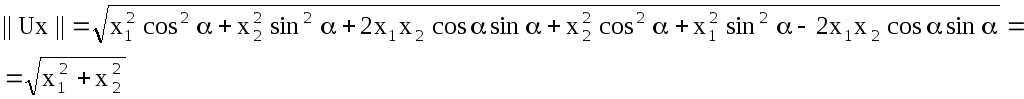
А следовательно, U– ортогональная матрица.

Задача: доказать, что линейный оператор φ, соответствующий матрице U, есть оператор поворота на угол α.

2)в пространствеRⁿ:

Рассмотрим матрицу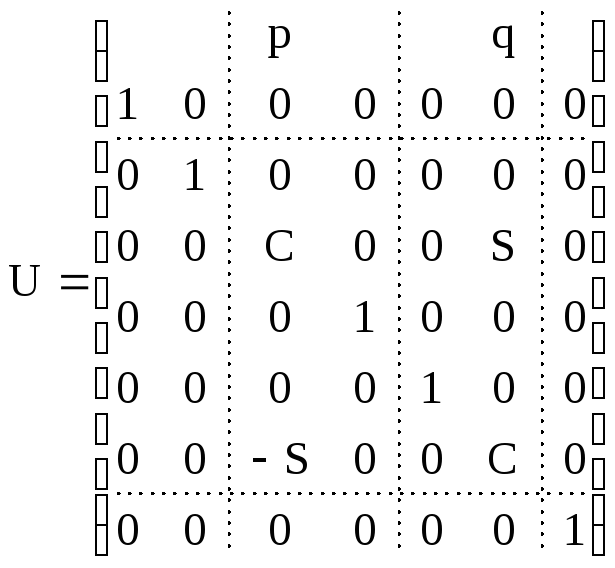, где с=cosα,s=sinα.

Т.е. u_pp =u_qq =c,u_pq = -u_qp =s,u_ii= |i≠p,q| =1,u_ij= |i,j≠p,q| = 0.

Задача: доказать, что линейный оператор Φ, соответствующий матрице U, есть оператор поворота на угол α вn-мерном пространстве.

§2. Вариационное свойство собственных значений

Матрица А неотрицательно определена, если.

Лемма Собственные числа неотрицательно определенной матрицы неотрицательны.

Доказательство

Пусть А – неотрицательно определенная матрица, λ₁– её собственное число.

Тогда .

Т.к. .

Что и требовалось доказать.

Матрица А симметричная , если.

Лемма 1 Если А симметрична, неотрицательно определена и (Ay,y)=0, тоAy=0. Геометрически: А не может сделать вектор у ортогональным самому себе, а может лишь обратить его в ноль.

Доказательство

Рассмотрим выражение (A(y+tz),y+tz),

где z– произвольный вектор;

t– вещественное, малое число (t<<1).

Если бы (Ay,z)≠0, то знак всего выражения можно было бы сделать отрицательным, выбирая знакt, что противоречило бы условию неотрицательной определенности А.

Значит, (Ay,z)=0.

Т.к. элеент zвыбирался произвольно, тоAy=0.

Что и требовалось доказать.

Рассмотрим выражение: .

Функция nпеременныхF(y)=(Ay,y) непрерывна на единичной сфере. Следовательно, по первой теореме ВейерштрассаF(y) достигает наS₁своих точных граней. Это означает, что.

Лемма 2 (вариационное свойство) Если А – симметричная матрица, то- собственное число матрицы А.

Доказательство

Из приведенных выше рассуждений и достигается в некоторой точке.

Т.к. , то ||y||=1, а значит.

Получим: .(*)

Из выбора точку y’ верно: (Ay,y)≤λ₁для любого вектораyизS₁.

Т.е. Последнее утверждение верно и для любого вектораxиз пространстваRⁿ. Т.е.- неотрицательно определенная матрица.

Следовательно, из (*), используя Лемму 1, получим:

, т.е. λ₁– собственное число матрицы А.

Что и требовалось доказать.