Глава2. Численное дифференцирование

Постановка задачи

Для дискретной функции f(x), заданной в узлахx₀..x_n, необходимо найти в определенном узле производную заданного порядка.

Данная задача относится к классу некорректно поставленных задач, т.к. погрешность поизводной интерполяционного многочлена может существенно превышать погрешность самой интерполяции. Т.о. к данной задаче требуется специальный подход.

Простейшие формулы погрешности

И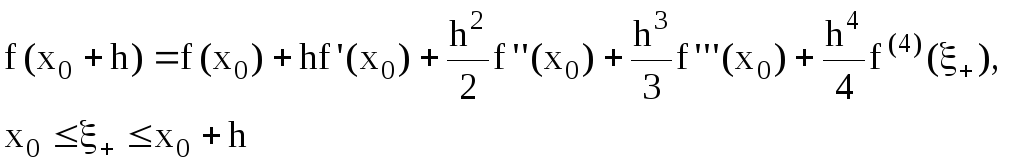з теории рядов Тейлора можно получить:

(1)

(2)

Из формулы (1) следует:

.

Из разности формул (1) и (2) получим:

- погрешность второго порядка для симметричной разности.

Сложив формулы (1) и (2):

- аппроксимация среднего значения (для достаточно гладких функций).

.(3)

Общий подход к решению поставленной задачи

Общая задача состоит в том, чтобы найти приближенную формулу:

и ее наилучшие коэффициентыC_k.(4)

Общность подхода в том, чтобы формула (4) была точна для некоторого набора функций. Так, например, формула (3) точна для любого многочлена степени, не превосходящей 4, т.к. для таких многочленов все производные, входящие в погрешность, равны 0.

Алгоритм нахождения формулы состоит в следующем.

Пусть выбраны функции φ₁(x)..φ_n+1(x) (по числу искомых коэффициентовC_k).

должны выполняться следующие равенства:

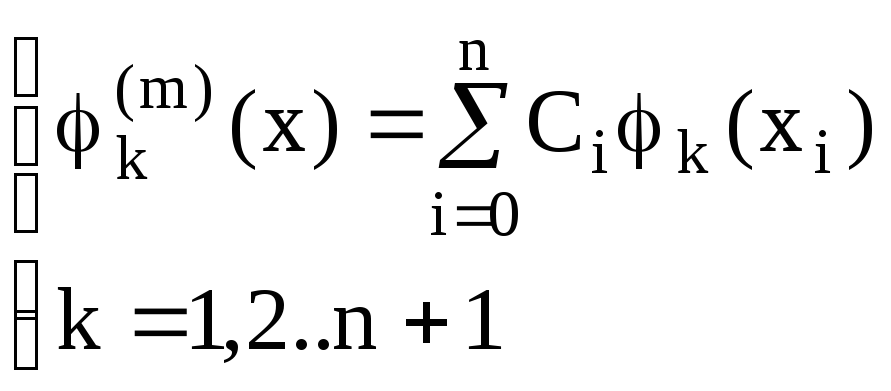- СЛАУ (n+1)ого порядка.

Определитель этой системы: .

Заметим, что при x_i<x_i+1,I=0..n-1,Δ≠0 (а значит система невырождена) тогда и только тогда, когда функцииφ₁(x)..φ_n+1(x) линейно независимы.

Погрешность

При численном дифференцировании приходится вычитать друг из друга близкие значения функции. Это приводит к уничтожению первых значащих цифр, т.е. к потере части достоверных знаков числа.

П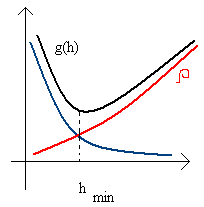усть значения функции известны с малой точностью ε. Ответим на вопрос: останется ли в решении исходной задачи хотьо один достоверный знак. Рассмотрим приближенное равенство:. При этом для достаточно гладких функций(погрешность первого порядка).

ρ определяет погрешность метода и неограниченно убывает при h→0. Но есть и неустранимая погрешность, связанная с погрешностью при вычислении функцииf(x):. Она неограниченно возрастает приh→0.

Таким образом, полная погрешность не превосходит . А значит, оптимальным будет шаг метода, соответствующий минимумуg(h).

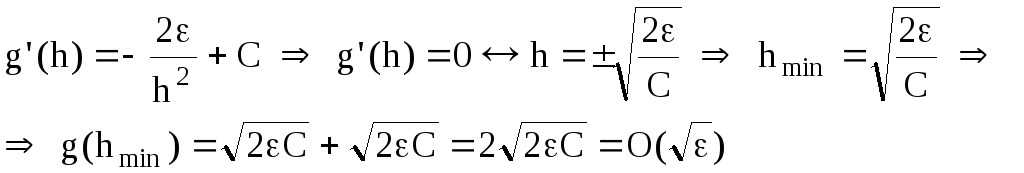
Меньший шаг невыгоден, а меньшая погрешность недостихима. Эта минимальная ошибка тем меньше, чем меньше погрешность входных данных.

Глава3. Численное интегрирование

Постановка задачи

Задача состоит в приближенном вычислении интеграла , например, по дискретным значениям функцииf(x) в узлахx₁..x_n , по замене функции ее аппроксимацией и т.д.

Так - интегральная сумма. Общий вид аппроксимирующих сумм: , гдеA_k– некоторые коэффициенты.

§1. Интерполяционные квадратурные формулы

1.Интерполяционные квадратурные формулы

Пусть требуется найти определенный интеграл ,

где f(x) – дискретная функция, заданная в узлахx₁…x_n;

q(x)>0 – весовая функция.

Тогда приближенная формула вычисления имеет вид:

(1)

Правая часть формулы (1) – квадратура.

Может быть применен следующий подход: функция f(x) аппроксимируется интерполяционным полиномомP_n-1(x) по узламx₁…x_n.

Получим для этого случая формулу (1) и квадратуру искомого интеграла.

Предполагается, что . Получим:.

При этом

- интерполяционный полином в Лагранжа,

- погрешность интерполяции.

Подставим в (1) вместо функции f(x) полиномP_n-1(x), получим:

-интерполяционная квадратура, где.(2)

Погрешность в этом случае представима в виде: .

По построению интерполяционная квадратурная формула точна,

если f(x)=P_n-1(x).

Теорема 1 Квадратурная формула (1) точна для любого многочленаP_k(x),

k≤n-1 тогда и только тогда, когда она – интерполяционная.

Доказательство

Пусть формула (1) точна для любого многочленаP_k(x),k≤n-1, т.е.

.

Докажем, что тогда A_kнаходятся по формуле (2).

Рассмотрим функции - многочлены (n-1) степени:

.

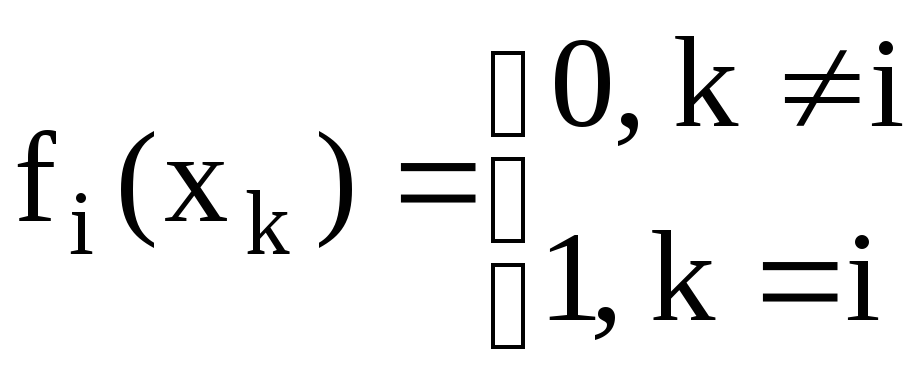Тогда выполняется равенство: , т.е.A_iвычисляются по формуле (2).

Пусть формула (1) интерполяционная, т.е.A_kвычисляются по (2). Докажем, что тогда (1) точна для любого многочленаP_k(x),k≤n-1.

Рассмотрим произвольный многочлен P_k(x),k=n-1.

Его представление в форме Лагранжа имеет вид:

.

Его интеграл:

.

С другой стороны, его квадратура

, гдеA_kвычисляются по формуле (2), т.еI=J.

Что и требовалось доказать.

Оценим погрешность квадратурной формулы интерполяционного типа:

, где.