§2. Применение квадратурных формул

Постановка задачи

Т.к. априорно треуется высокая гладкость функции, и вычисление интерполяционного многочлена сложно, а также сложно увеличивать число узлов (т.е. уменьшать шаг), то для вычисления интеграла используется следующий метод.

Отрезок [a;b] разбивается на узлыa=x₀<..<x_n=b(для простоты шагhпостоянен). Следовательно, исходный интеграл разбивается на сумму интегралов:.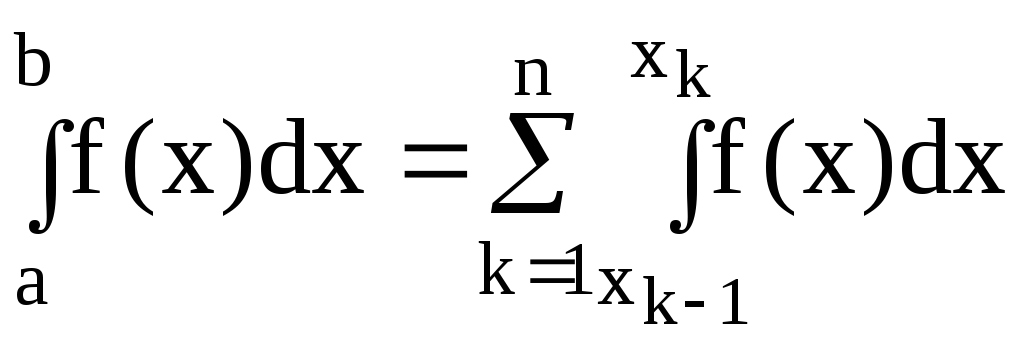

Теперь достаточно построить интерполяционную квадратурную формулу для интеграла на малом отрезке [x_k-1;x_k], т.е. более низкого порядкаm, чем для интеграла по всему отрезку [a;b].

1.Метод прямоугольников (m=0)

На отрезке [x_k-1;x_k] функцияf(x) заменяется по некоторому определенному значению (поf(x_k-1) – метод левых; поf(x_k) – метод правых; поf((x_k+x_k-1)/2) – методcрединных прямоугольников) многочленомP₀(x,k).

Рассмотрим метод левых прямоугольников.

Применяется квадратурная формула:

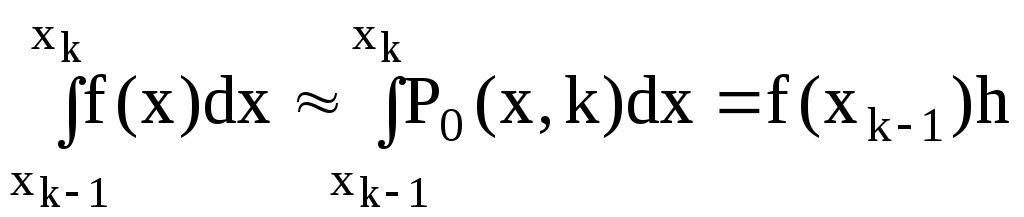, гдеh=x_k –x_k-1.

Получим общую квадратурную формулу:

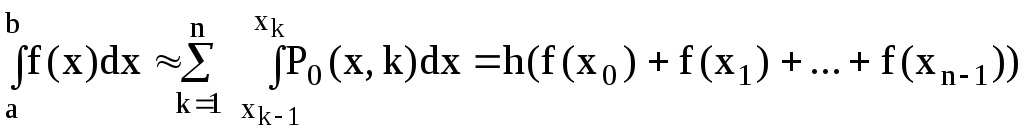
Оценим погрешность данного метода. Вообще в задаче алгебраической интерполяции f(x) многочленом Р_n(x) погрешностьR_n(x) имеет видO(hⁿ⁺¹)

1) Локальная погрешность аппроксимации

для многочлена Р₀(х):R₀(x)=O(h¹)

2)Локальная погрешность интегрирования

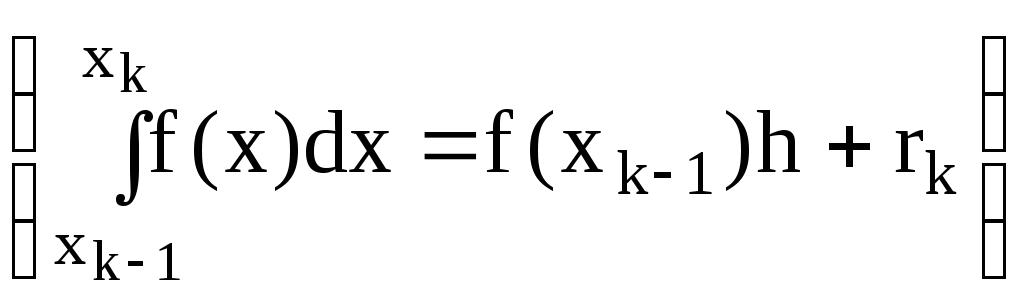
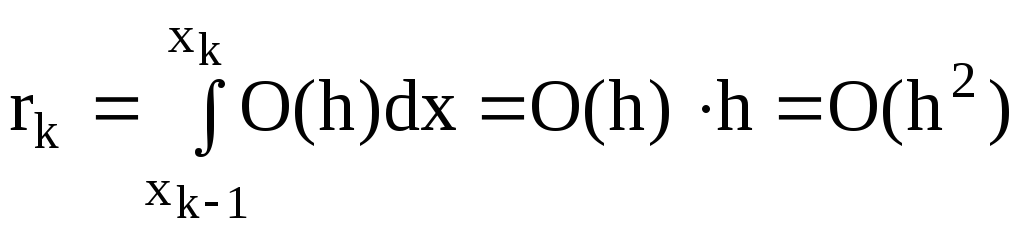
3)Общая погрешность интегрирования

Т.е. метод прямоугольников - первого порядка точности.

2. Метод трапеций (m=1)

На отрезке [x_k-1;x_k] функцияf(x) заменяется по значениям в узлахx_k-1,x_k многочленомP₁(x,k).

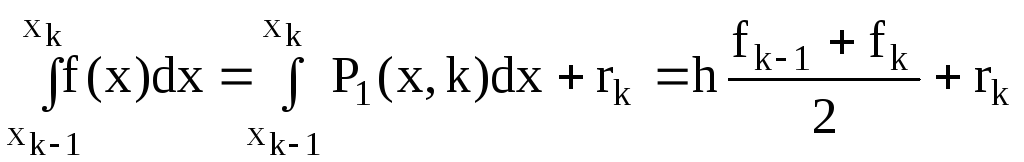
Общая формула:

Погрешность:

1) O(h²) для Р₁(х)

2)

3)

Т.е. метод - второго порядка точности.

3. Метод парабол (m=2)

На отрезке [x_k-1;x_k] функцияf(x) аппроксимируется параболой. Для этого берутся значения функции в точкахx_k-1,x_{k ,} (x_k+x_k-1)/2).

Обозначим интерполяционный полином как P₂(x,k).

Тогда:

.

Оценим погрешность данного метода.

1) Локальная погрешность аппроксимации

для многочлена Р₂(х):R₂(x)=O(h³)

2)Локальная погрешность интегрирования

3)Общая погрешность интегрирования

Т.е. метод прямоугольников - третьего порядка точности.

Коэффициенты a_1k,a_2kиa_3kможно найти, воспользовавшись представлением функции приближенно в виде интерполяционнго многочлена Лагранжа:

_.

§3. Метод Монте-Карло (метод статистических испытаний)

Всякий интеграл можетбыть сведен линейной заменой масштабов к интегралу вида, где 0≤f(x)≤1.

Из теории вероятностей:

1)случайная величина ξ равномерно распределена на [0;1], если. В частности.

2)двумерная случайная величина (ξ ,η) равномерно распределена на [0;1]×[0;1], если. При этом если ξ ,η равномерно распределены на [0;1], то (ξ ,η) равномерно распределена на [0;1]×[0;1].

Т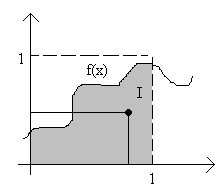аким образом, для вычисления интеграла(т.е. для вычисления заштрихованной области) достаточно определить вероятность того, что точка (x,y) попадет в эту площадь (область, где (x,y) – равномерно распределенная случайная величина).

В ЭВМ существует датчик псевдослучайных чисел, значениями которого являются случайные числа, равномерно распределенные на [0;1].

Алгоритм:

1)генерируются равномерно распределенные на [0;1] случайные числа ξ_k, η_k

2)вычисляетсяf(ξ_k)

3)сравниваетсяf(ξ_k) и η_kи подсчитывается числоNнеравенствf(ξ_k) > η_k,k=1..M.

При достаточно большом числе испытаний M>>1 .

Ответ, полученный с помощью данного метода носит вероятностный характер и может сколь угодно сильно отличаться от точного значения интеграла. Однако с вероятностью 99,7% ошибка не превосходит (- дисперсия от среднеарифметического). При реальных испытаниях ошибка обычно не превосходит. С увеличением числа испытаний погрешность ответа будет убывать римерно как.