§4. Правило Рунге практической оценки погрешности

Величины погрешности численного интегрирования зависит как от шага h, так и от гладкости подинтегральной функции. Если величина погрешности велика, то ее можно уменьшить путем измельчения сетки на данном отрезке [x_k-1;x_k]. Для этого необходимо уметь апостериорно (т.е. после проведения расчета) оценивать погрешность. Правило Рунге позволяет произвести такую оценку.

Представим интеграл в виде приближенной формулы:

Заметим, что SиRзависят от шагаh, т.е. от числа точек разбиенияn. ТогдаS=S_n,R=R_n.

Будем считать, что дана априорная погрешность (предполагаемая):

Если С известно, то можно заранее для нужной точности указать число точек разбиения и т.п.

Если же С неизвестно, то используют правило Рунге:

1. Производят 2 вычисления приближенного значения интеграла приn=n₁иn=n₂(обычноn₂=2n₁).

2. Таким образом, будет получено:

I=S_n1+R_n1; I=S_n2+R_n2

Вычитая из первого равенства второе, получим:

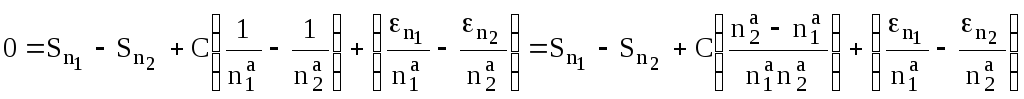Отсюда,.

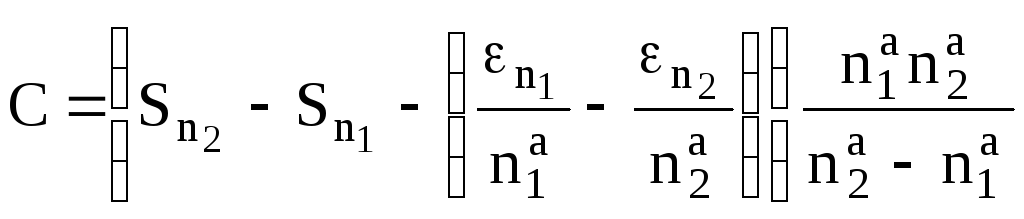Подставим CвR_n1иR_n2:

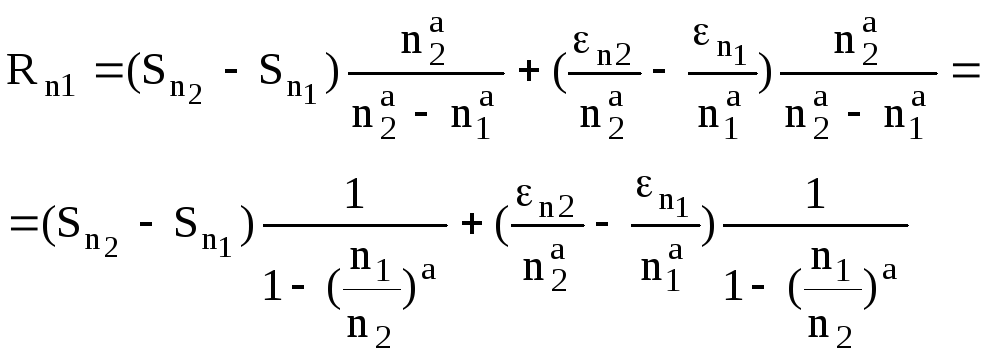
При этом выражение .

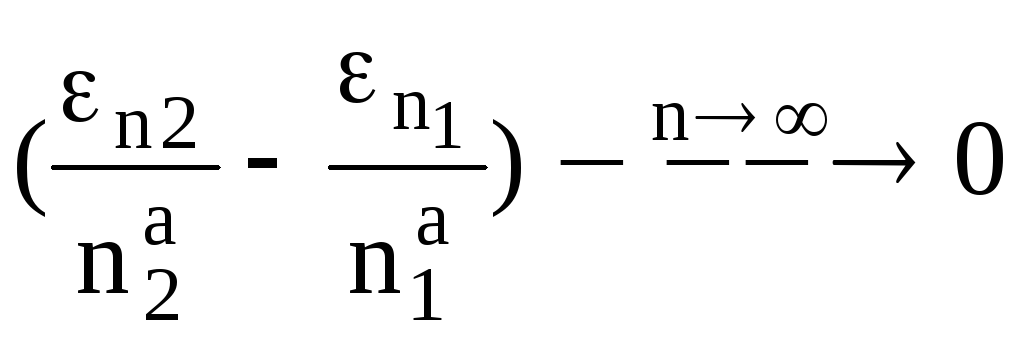Таким образом, , т.к.невелико (обычно, а=2).

Это и есть правило Рунге:

В выбранной квадратурной формуле берется некоторое число точек разбиения n₁и вычисляетя соответствующее ему значение интеграла.

Затем вычисляется приближенное значение, соответствующее числу точек разбиения n₂>n₁. Если модуль разности между ними не превышает требуемой точности, то вычисления останавливаются. В противном случае, процедуру необходимо повторить.

В качестве ответа обычно берут S_n2или линейную комбинациюS_n1, S_n2.

Глава4. Алгебраическая проблема собсвенных значений

Постановка задачи

Пусть A=(a_ik) – вещественная матрица порядкаn×nпространстваRⁿ. Элементы пространстваRⁿимеют вид:x=(x₁..x_n)^T.

Скалярное произведение векторов в Rⁿ: .

Норма вектора в пространстве Rⁿ: .

Число λ – собственное число матрицы А, если существует нетривиальный векторx¹≠0:Ax=λx. При этомx¹ – собственный вектор А. (1)

Множество всех собственных чисел матрицы – её спектр.

Спектральная задача – задача нахождения всех или нескольких собственных чисел матрицы и, возможно, соответствующих им собственных векторов.

Пусть λ₁– собственное число матрицы А. Перепишем уравнение (1) в виде:

.

Многочлен вида: 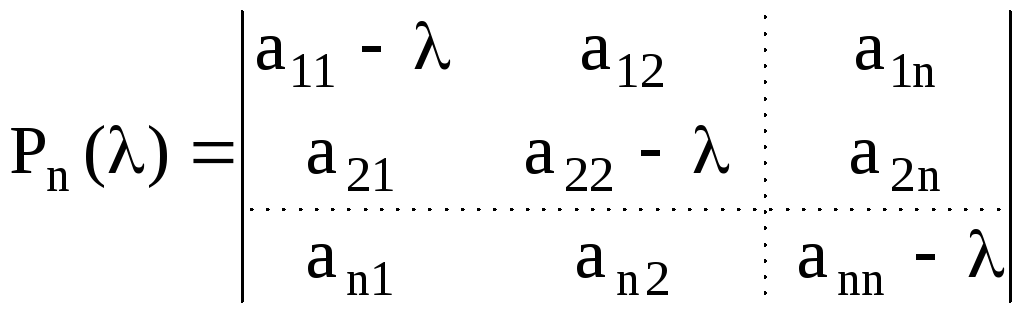-характеристический многочлен матрицы А.

Т.о. если λ – собственное число матрицы А, то λ – корень характеристического многочлена матрицы А. Верно и обратное.

Утверждение Любая матрица А порядкаn×nимеет хотя бы один собственный вектор и имеетnсобственных чисел (могут быть как различными, так и кратными).

Из сказанного: задача нахождения собственных чисел матрицы А сводится к задаче нахождения корней её характеристического многочлена, т.е. решения уравнения P_n(λ) = 0.

Некорректность спектральной задачи

При исследовании спектральной задачи было выяснено, что она неустойчива. Приведем пример. Рассмотрим матрицу порядка 20×20:

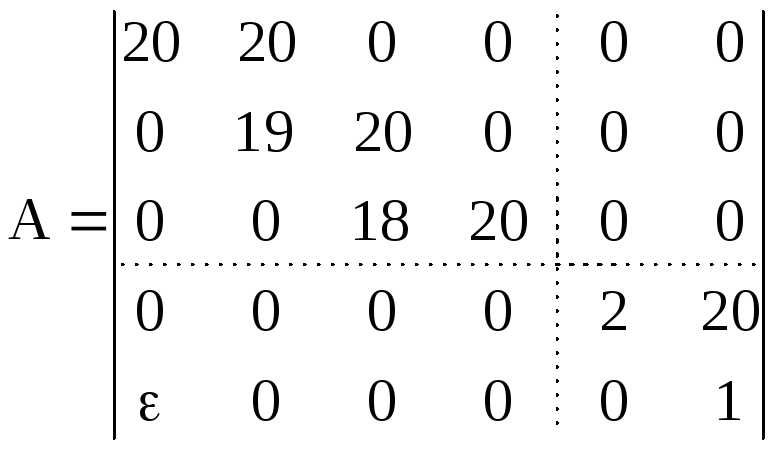, где ε – малое возмущение нулевого элемента.

Характеристический многочлен матрицы А имеет вид: .

Рассмотрим два случая:

1)ε=0 Тогда младший коэффициентP_n(λ)a₀=20!≈2,5×10¹⁸. Собственные числа матрицы Аλ_k=1..20.

2)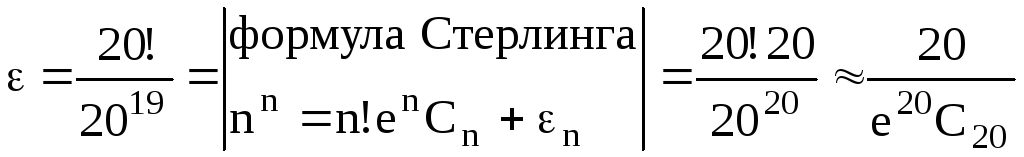- малое число.

При этом a₀=0 и возникает новое собственное число матрицы А λ=0.

Т.о. как коэффициенты, так и корни характеристического многочлена могут быть очень чувствительны к малым погрешностям матричных элементов, что означает слабую устойчивость спектральной задачи.