
- •Основные понятия и определения
- •1.1. Переключательные функции одного и двух аргументов
- •1.3. Представление переключательной функции в виде многочленов.
- •1.4. Пять классов переключательных функций. Теорема о функциональной полноте
- •Линейные
- •1.5. Функционально полные системы логических функций.
- •1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ГРАФОВ
- •Алгоритм построения минимального каркаса
- •Обоснование алгоритма
- •7. ЭЙЛЕРОВЫ ЦЕПИ И ЦИКЛЫ
- •Алгоритм построения эйлерова цикла
- •Обоснование алгоритма
- •Алгоритм Флойда

|
|
|
|
Переключательные функции двух аргументов |
Таблица 1.6 |
|||||
|
|
|
|
|
|
|||||
x |
0 |
0 |
1 |
1 |
Линейные |
Сохраня- |
Сохраня- |
Монотон- |
|
Самодвой- |
y |
0 |
1 |
0 |
1 |
ющие 0 |
ющие1 |
ные |
|
ственные |
|
|
|
|
|
|
(TL) |
(T0) |
(T1) |
(TM) |
|
(Ts) |
f0(x,y) |
0 |
0 |
0 |
0 |
* |
* |
|
* |
|
|
f1(x,y) |
0 |
0 |
0 |
1 |
|
* |
* |
* |
|
|
f2(x,y) |
0 |
0 |
1 |
0 |
|
* |
|
|
|
|
f3(x,y) |
0 |
0 |
1 |
1 |
* |
* |
* |
* |
|
* |
f4(x,y) |
0 |
1 |
0 |
0 |
|
* |
|
|
|
|
f5(x,y) |
0 |
1 |
0 |
1 |
* |
* |
* |
* |
|
* |
f6(x,y) |
0 |
1 |
1 |
0 |
* |
* |
|
|
|
|
f7(x,y) |
0 |
1 |
1 |
1 |
|
* |
* |
* |
|
|
f8(x,y) |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
f9(x,y) |
1 |
0 |
0 |
1 |
* |
|
* |
|
|
|
f10(x,y) |
1 |
0 |
1 |
0 |
* |
|
|
|
|
* |
f11(x,y) |
1 |
0 |
1 |
1 |
|
|
* |
|
|
|
f12(x,y) |
1 |
1 |
0 |
0 |
* |
|
|
|
|
* |
f13(x,y) |
1 |
1 |
0 |
1 |
|
|
* |
|
|
|
f14(x,y) |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
f15(x,y) |
1 |
1 |
1 |
1 |
* |
|
* |
* |
|
|
Может показаться, что любая функционально полная система должна содержать не менее пяти переключательных функций. Однако ввиду того, что многие переключательные функции удовлетворяют одновременно нескольким требованиям, предъявляемым теоремой о функциональной полноте, количество независимых переключательных функций, входящих в функционально полную систему, всегда меньше пяти1.
В функционально полную систему переключательных функций двух аргументов в соответствии с теоремой о функциональной полноте должны входить такие функции, которые совместно перекрывают клетками без крестиков колонки TL, T0, T1, TM, TS (табл. 1.6). Из переключательных функций, сведенных в табл. 1.6, можно составить различные функционально полные системы. Рассмотрим некоторые из них.
1.f14 (х, у)=х у; эта переключательная функция одна обладает свойством функциональной полноты, так как является нелинейной, немонотонной, несамодвойственной, не сохраняет нуль и единицу. Следовательно, любая переключательная функция может быть представлена через функции f14 (х, у), и поэтому любая сложная функция
1 Система переключательных функций называется независимой, если ни одна из входящих в нее функций не выражается через другие функции этой же системы с помощью операций суперпозиции или подстановки аргументов.
16
может быть представлена через эту функцию;
2.f8 (х, у)=х↓у; эта функция, так же как и функция f14 (х, у), одна обладает свойством функциональной полноты;
3.f13 (х, у)=x→y и f0 (х, у)=0 или f11 (х, у)=y→x и f0 (х, у)=0, т. е. импли-
кация и константа нуль;
4.f6 (х, у)=х у; f1 (х, у)=x y и f15 (х, у)=1, т. е. сумма по модулю два,
произведение и константа единица. Функциональная полнота этой
системы следует не только из теоремы о функциональной полноте, но и из доказанной ранее теоремы Жегалкина (см. п. 1.3.2).
В связи с тем, что существует большое число различных функционально полных систем переключательных функций, возникает проблема выбора функционально полной системы, представляющей наибольший практический интерес.
1.5. Функционально полные системы логических функций.
Из множества функционально полных наборов рассмотрим только те, которые имеют наибольшее практическое значение.
1.5.1. Основная функционально полная система логических функ-
ций. Наибольшее распространение получил набор, в состав которого входят три логические функции:
•f10 – инверсия (логическая связь НЕ, логическое отрицание);
•f1 – конъюнкция (логическая связь И, логическое умножение),
•f7 – дизъюнкция (логическая связь ИЛИ, логическое сложение).
Этот набор получил название функционально полной системы логи-
ческих функций (ОФПС). Из теоремы о функциональной полноте следует, что основная функционально полная система логических функций является избыточной, так как условиям теоремы отвечают наборы функций f10 и f1 или f10 и f7. Свойства этих функций были рассмотрены ранее.
Из определения представления переключательной функции в виде дизъюнктивной или конъюнктивной нормальной формы следует, что эти представления реализуются в основной функционально полной системе логических функций.
1.5.2. Законы алгебры логики в ОФПС и их следствия. В алгебре логики имеются четыре основных закона, регламентирующих порядок производства операций НЕ, И, ИЛИ в любом логическом выражении:
•переместительный (коммутативный);
•сочетательный (ассоциативный);
•распределительный (дистрибутивный);
•инверсии (правило Де Моргана).
Переместительный закон. Этот закон справедлив как для дизъюнк-
17
ции, так и для конъюнкции: |
|
|
x1 x2 = x2 x1; |
x1 x2 = x2 x1. |
(5.1) |
Справедливость выражения (5.1) нетрудно доказать простой подстановкой в него различных значений x1 и x2. Поскольку любую перестановку большего количества слагаемых можно свести к последовательности перестановок слагаемых в отдельных парах, то переместительный закон будет справедлив при любом числе слагаемых.
Сочетательный закон. Этот закон, так же как и переместительный, является симметричным, т. е. справедливым и для дизъюнкции, и для конъюнкции:
x1 x2 x3 = x1 (x2 x3) = (x1 x2) x3= x2 ( x1 x3); (5.2)
x1 x2 x3 = x1 x2 x3) = (x1 x2) x3= x2 ( x1 x3).
Доказательство этого закона также не представляет никаких трудностей и может быть выполнено простой подстановкой.
Распределительный закон. В отличие от обычной алгебры алгебра логики симметрична. В ней справедливы два распределительных закона: для логического умножения относительно логического сложения (распределительный закон 1-го рода) и для логического сложения относительно логического умножения (распределительный закон 2-го рода).
1. Распределительный закон 1-го рода записывается следующим образом:
(x1 x2) x3=(x1 x3) |
( |
x2 |
x3) |
. |
(5.3)
Справедливость формулы (5.3), а также и ее более общего случая, когда в скобках заключена сумма любого количества слагаемых, можно доказать путем установления идентичности условий обращения в 0 или 1 ее левой и правой частей. Условием обращения в нуль левой части выражения (5.3) состоит в том, чтобы нулю равнялся либо один аргумент х3, либо одновременно аргументы x1 и x2. Условия обращения в нуль правой части выражения (5.1) такие же. Следовательно, распределительный закон 1-го рода справедлив для алгебры логики.
2. Распределительный закон 2-го рода имеет вид
(x1 x2) x3=(x1 x3) ( x2 x3). (5.4)
Cправедливость формулы (5.4) (при любом количестве аргументов) нетрудно доказать посредством установления идентичности условий обращения обеих ее частей в единицу.
Закон инверсии (правило Де Моргана). Этот закон, так же как и все предыдущие, симметричен относительно логических сложения и умножения.
1. Отрицание логической суммы нескольких аргументов равно логическому произведению отрицаний этих же аргументов:
18
|
= x1 x2 xn . |
(5.5) |
x1 x2 ... xn |
Доказательство закона не представляет трудностей, поскольку условие обращения в нуль как левой, так и правой частей выражения (5.5) состоит в том, чтобы был истинным хотя бы один аргумент.
2. Отрицание логического произведения нескольких аргументов равно логической сумме отрицаний этих же аргументов:
|
= x1 x2 xn . |
(5.6) |
x1 x2 ... xn |
Справедливость этого закона следует из того, что условие обращения в единицу обеих частей формулы (5.6) заключается в том, чтобы был ложным хотя бы один аргумент.
Следствия из законов алгебры логики. Из доказанных выше за-
конов можно вывести ряд следствий, которые сформулируем в виде правил.
Правило выполнения совместных логических действий (правило старшинства логических функций).. При решении логических задач при-
ходится встречаться с выражениями, содержащими действия отрицания, конъюнкции и дизъюнкции в любом сочетании. По аналогии с арифметическими действиями будем считать отрицание логическим действием первой ступени (старшей логической операцией), конъюнкцию — действием второй ступени, а дизъюнкцию — действием третьей ступени (младшей логической операцией).
Старшинство операции инверсии вытекает из закона инверсии, в соответствии с которым логическая сумма отрицаний некоторых аргументов не равна отрицанию их суммы (это справедливо и для логического произведения). Это значит, что ни операцию дизъюнкции, ни операцию конъюнкции нельзя проводить, игнорируя знак отрицания над каким-либо из логических аргументов, т. е. операцию отрицания надо проводить в первую очередь.
Относительно операций логического сложения и умножения на основании симметричности законов алгебры логики можно сказать, что они «равноправны». Из этого следует, что можно условиться считать более старшей операцией любую из них, но, приняв какое-либо условие, надо придерживаться его все время. На практике оказалось удобнее считать более старшей операцию логического умножения, так как это соответствует правилам обычной алгебры и для нас более привычно.
На основе изложенного можно сформулировать следующее правило выполнения совместных логических действий: если в логическом выра-
жении встречаются только действия одной и той же ступени, то их принято выполнять в том порядке, в котором они написаны; если в логическом выражении встречаются действия различных ступеней, то сначала принято выполнять действия первой ступени, затем — второй, и
19

только после этого — третьей. Всякое отклонение от этого порядка должно быть обозначено скобками.
Правило склеивания. Прежде чем сформулировать само правило, введем некоторые новые понятия. Если имеется некоторый конечный набор логических аргументов x1, x2, … xn, то логическое произведение любого их числа называется элементарным в том случае, когда сомножителями в нем являются либо одиночные аргументы, либо отрицания одиночных аргументов. Так, например, f1(х1, х2, x3, х4)= х1 х2 x3 х4 — элементарное произведение (элементарная конъюнкция); f2 (x1, x2 , x3 , x4 ) = x1 x2 x3 x4 —
не является элементарным произведением.
Cимвол любого аргумента в элементарной конъюнкции может встречаться только один раз, поскольку произведение аргумента самого на себя равно этому же аргументу, а произведение аргумента на свое отрицание равно нулю. Количество сомножителей в элементарной конъюнкции называется ее рангом.
Два элементарных произведения одинакового ранга r называются соседними, если они являются функциями одних и тех же аргументов и отличаются только знаком отрицания (инверсии) одного из сомножителей. Например, элементарные конъюнкции
f1(х1, х2, x3, х4)= х1 х2 x3 х4 и f3(х1, х2, x3, х4)= x1 x2 x3 x4
являются соседними, так как отличаются только одной инверсией в переменной x2, а элементарные конъюнкции
f3(х1, х2, x3, х4)= x1 x2 x3 x4 и f4(х1, х2, x3, х4)= x1 x2 x3 x4
соседними не являются.
Правило склеивания для элементарных конъюнкций может быть сформулировано следующим образом: логическую сумму двух соседних произведений некоторого ранга r можно заменить одним элементарным произведением ранга r-1, являющимся общей частью исходных слагаемых.
Это правило является следствием распределительного закона 1-го рода и доказывается путем вынесения за скобку общей части слагаемых, являющихся соседними конъюнкциями. Тогда в скобках остается логическая сумма некоторого аргумента и его инверсии, равная единице, что и доказывает справедливость правила.
Например,
x1 x2 x4 x5 x1 x2 x4 x5 = x2 x4 x5 (x1 x1 ) = x2 x4 x5 .
Поскольку алгебра логики является симметричной, то все определения, данные для конъюнкции, будут справедливы и для дизъюнкции.
Если имеется некоторый конечный набор логических аргументов, то логическая сумма (дизъюнкция), зависящая от любого их числа, называется элементарной в том случае, когда слагаемыми в ней являются либо одиночные аргументы, либо отрицания одиночных аргументов.
20
Количество слагаемых в элементарной дизъюнкции называется ее рангом. Две элементарные суммы одинакового ранга называются соседними, если они являются функциями одних и тех же аргументов и отличаются только знаком отрицания (инверсии) одного из слагаемых.
Правило склеивания двух элементарных дизъюнкций формулируется так: логическое произведение двух соседних сумм некоторого ранга r можно заменить одной элементарной суммой ранга r-1, являющейся общей частью исходных сомножителей.
Это правило является следствием распределительного закона 2-го рода и применяется для упрощения логических выражений.
Например:
(x1 x3 x5 x6 ) (x1 x3 x5 x6 ) =
= (x1 x3 x6 ) (x5 x5 ) = (x1 x3 x6 ).
Правило поглощения. Так же как и склеивание, поглощение может быть двух видов. Правило поглощения для двух элементарных конъюнк-
ций формулируется так: логическую сумму двух элементарных произведений разных рангов, из которых одно является собственной частью другого, можно заменить слагаемым, имеющим меньший ранг.
Это правило является следствием распределительного закона 1-го рода. Доказывается оно посредством вынесения за скобку общей части слагаемых. В скобках останется логическая сумма некоторого выражения и единицы, равная в свою очередь также единице, что и доказывает справедливость правила. Например,
x1 x2 x4 x5 x7 x2 x4 x5 = x2 x4 x5 (x1 x7 1) = x2 x4 x5 .
Правило поглощения для двух элементарных дизъюнкций: логи-
ческое произведение двух элементарных сумм разных рангов, из которых одна является общей частью другой, можно заменить сомножителем, имеющим меньший ранг.
Это правило является следствием распределительного закона 2-го рода и также находит широкое применение для упрощения логических функций.
Правило развертывания. Это правило регламентирует действие, обратное склеиванию. Иногда требуется представить некоторое логическое выражение в виде совокупности конституент единицы или конституент нуля. Если членами преобразуемого выражения являются элементарные конъюнкции, то переход от них к конституентам единицы производится в три этапа по следующему правилу:
•в развертываемую элементарную конъюнкцию ранга r в качестве дополнительных сомножителей вводится п-r единиц, где п — ранг конституенты;
21
•каждая единица представляется в виде логической суммы неко-
торой, не имеющейся в исходной конъюнкции переменной и ее отрицания: xi xi =1;
•производится раскрытие всех скобок на основе распределительного закона первого рода, что приводит к развертыванию исходной элементарной конъюнкции ранга r в логическую сумму кон-
ституент единицы.
Пример 5.1. Развернуть элементарную конъюнкцию f(x1,x2,x3,x4) = =x1 x3 в логическую сумму конституент единицы.
Решение. Ранг конституенты единицы для данной функции равен 4. Производим развертывание исходной конъюнкции поэтапно в соответствии с правилом развертывания:
1-й этап— f(x1,x2,x3,x4) = x1 1 x3 1.
2-й этап — f(x1,x2,x3,x4) = x1 (x2 x2 ) x3 (x4 x4 ). 3-й этап — f(x1,x2,x3,x4)=
= x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 , что и тре-
бовалось получить.
Если членами преобразуемого выражения являются элементарные дизъюнкции, то переход от них к конституентам нуля производится также
втри этапа по следующему правилу:
•в развертываемую элементарную дизъюнкцию ранга r в качестве дополнительных слагаемых вводится п-r нулей;
•каждый нуль представляется в виде логического произведения не-
которой, не имеющейся в исходной дизъюнкции переменной, и ее отрицания: xi xi = 0;
•получившееся выражение преобразуется на основе распределительного закона второго рода таким образом, чтобы произвести развертывание исходной элементарной дизъюнкции ранга r в логиче-
ское произведение конституент нуля.
Пример 5.2. Развернуть элементарную дизъюнкцию f(x1,x2,x3,x4)= =x3 x4 в логическое произведение конституент нуля.
Решение. Ранг конституенты нуля п = 4. Далее производим развертывание исходной дизъюнкции поэтапно в соответствии с правилом развертывания:
1-й этап — f(x1,x2,x3,x4) =0 0 x3 x4;
2-й этап — f(x1,x2,x3,x4) = (x1 x1) (x2 x2 ) x3 x4. 3-йэтап—f(x1,x2,x3,x4)=
=(x1 x2 x3 x4 ) (x1 x2 x3 x4 )
(x1 x2 x3 x4 ) (x1 x2 x3 x4 ),
что и требовалось получить.
22

Проверить правильность проведенных преобразований можно при помощи правила склеивания.
1.5.3. Функционально полные системы логических функций.
Анализ принадлежности переключательных функций замкнутым классам показывает, что существуют две переключательные функции f8 и f14, не принадлежащие ни одному классу. Согласно теореме о функциональной полноте, каждая из этих функций образует функционально полную систему логических связей и используя только одну из них можно представить любую, сколь угодно сложную переключательную функцию.
Операция Пирса (стрелка Пирса) реализует функцию, которая принимает значение, равное единице только в том случае, когда все ее аргументы равны 0 (ИЛИ-НЕ), что может быть записано в ОФПС для функции двух переменных следующим образом:
f8 (x1, x2 ) = x1 ↓ x2 = |
|
|
(5.7) |
x1 x2 . |
|||
Используя операции суперпозиции и подстановки можно показать, что операция Пирса может быть реализована для n аргументов:
f8 (x1, x2 ,..., xn ) = x1 ↓ x2 ↓ ↓ xn = |
|
|
(5.8) |
x1 x2 ... xn . |
|||
Для представления переключательной функции в базисе Пирса необходимо выполнить следующие действия:
•представить переключательную функцию f в конъюнктивной нормальной форме;
•полученное выражение представить в виде f (поставить два знака
отрицания);
•применить правило Де Моргана.
Например, для того чтобы представить функцию
f(x1, x2 , x3 , x4 ) = (x1 x2 ) (x3 x4 )
вбазисе Пирса, необходимо выполнить следующие преобразования:
f (x1, x2 , x3 , x4 ) = (x1 x2 ) (x3 x4 ) = (x1 x2 ) (x3 x4 ).
Для представления полученного выражения в базисе Пирса воспользуемся соотношением (5.7):
f (x1, x2 , x3 , x4 ) = (x1 ↓ x2 ) ↓ (x3 ↓ x4 ) .
Операция Шеффера (штрих Шеффера) реализует функцию, которая принимает значение, равное нулю, только в том случае, когда все ее аргументы равны 1 (И-НЕ), что может быть записано в ОФПС для функции двух переменных следующим образом:
f8 (x1, x2 ) = x1 x2 = x1 x2. |
(5.9) |
Используя операции суперпозиции и подстановки, можно показать, что операция Пирса может быть реализована для n аргументов:
f(x1,x2,…,xn)= x1 x2 … xn = |
|
|
(5.10) |
x1 x2 ... xn . |
|||
23

Для представления переключательной функции в базисе Шеффера необходимо выполнить следующие действия:
•представить переключательную функцию f в дизъюнктивной нормальной форме;
•полученное выражение представить в виде f (поставить два знака
отрицания);
•применить правило Де Моргана.
Например, для того чтобы представить функцию
f(x1, x2 , x3 , x4 ) = (x4 x2 ) (x3 x1) (x4 x3 )
вбазисе Шеффера, необходимо выполнить следующие преобразования:
f (x1, x2 , x3 , x4 ) = (x4 x2 ) (x3 x1) = (x4 x2 ) (x3 x1).
Для представления полученного выражения в базисе Шеффера воспользуемся соотношением (5.9):
f(x1,x2,x3,x4)=(x4 x2) (x3 x1).
2. МИНИМИЗАЦИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ
2.1. Вхождение функции в функцию. Импликанты
Понятием "минимизация переключательных функций" объединяется ряд процедур, выполнение которых направлено на получение наиболее компактной, минимальной в некотором смысле формы представления переключательной функции. Как правило, в качестве критерия минимальности переключательной функции используется число букв в логическом выражении. Действительно, любые две рядом стоящие буквы связаны между собой знаком какой-либо логической операции. Поэтому, чем меньше букв в логическом выражении, тем меньше логических операций необходимо для реализации этого выражения, тем меньше логических элементов требуется для построения соответствующей комбинационной схемы. Это ведет к минимуму веса устройства, минимуму стоимости и т.д.
Как правило, все алгоритмы минимизации начинаются с приведения переключательной функции к канонической форме, в качестве которой используются совершенные дизъюнктивная и конъюнктивная нормальные формы. Основные этапы минимизации приведены на рис. 2.1.
Смысл минимизации переключательных функций заключается в поиске совокупности таких элементарных конъюнкций (дизъюнкций), которые своими единицами (нулями) накрывали бы как можно большее число единиц (нулей) среди значений заданной переключательной функции.
24
Понятие вхождения одной переключательной функции в другую является весьма существенным, поскольку именно оно во многом определяет "механизм" минимизации переключательных функций.
Будем говорить, что переключательная функция ϕ(х1, х2, …, хn) входит в переключательную функцию f(х1, х2, …, хn), если функция ϕ накрывает своими нулями все нули функции f, а единицы функции f накрываются как нулями, так и единицами функции ϕ; т.е. функция ϕ должна иметь нулевых значений не меньше, чем функция f, и, кроме того, нули функции ϕ должны быть определенным образом расположены.
Определение 2.1. Функция ϕ(х1, х2, …, хn), входящая в функцию f(х1,
х2, …, хn) называется импликантой этой функции.
Применение термина "импликанта" связано с переключательной функцией двух переменных f13(x,y) = x→ y, именуемой импликацией. Воспользовавшись таблицей истинности для функции f13(x,y) можно убедиться в том, что выражение ϕ→f тождественно равно единице, т.е. является всегда истинным только тогда, когда функция ϕ входит в функцию f. Тот факт, что ϕ входит в f обозначается следующим образом: ϕ f. Рассмотрим таблицу истинности для некоторых функций двух переменных.
x1 |
0 |
0 |
1 |
1 |
x2 |
0 |
1 |
0 |
1 |
f6(х1, х2) |
0 |
1 |
1 |
0 |
f4(х1, х2) |
0 |
1 |
0 |
0 |
f2(х1, х2) |
0 |
0 |
1 |
0 |
f0(х1, х2) |
0 |
0 |
0 |
0 |
f3(х1, х2) |
0 |
0 |
1 |
1 |
Очевидно, что f4(x1,x 2) f6(x1,x 2); f2(x1,x 2) f6(x1,x 2); f0(x1,x 2) f6(x1,x 2),
т.е. функции f4, f2, f0 являются импликантами функции f6. Кроме того, очевидно, что в соответствии с определением понятия вхождения функции в
функцию f6(x,y) f6(x,y). Если сравнить значения функции f6(x,y) и f3(x,y) на всех наборах аргументов, то можно заключить, что f3(x,y) f6(x,y), т.е. функция f3 в функцию f6 не входит.
Определение 2.2. Функция ϕ(х1, х2, …, хn) называется простой импликантой функции f(х1, х2, …, хn), если сама функция ϕ входит в функцию f, но никакая собственная часть функции ϕ в f не входит.
Если некоторая импликанта представлена, например, в виде элементарного логического произведения, то ее собственные части могут быть получены путем исключения из данного произведения одного или нескольких
25

сомножителей. Например, произведение x1 x2 x3 имеет собственные части x1, x2, x3, x1 x2, x1 x3 и x2 x3.
Предположим, что выполняется следующее условие:
x1 x2 x3 x4 f(х1, х2, х3, х4), x1 x3 f(х1, х2, х3, х4),
x1 f(х1, х2, х3, х4), x3 f(х1, х2, х3, х4),
т.е. элементарное произведение x1 x3 является простой импликантой функции f(х1, х2, х3, х4). Символ означает, что в данном случае условие вхождения одной функции в другую не выполняется.
Простые импликанты представляют собой самые короткие элементарные произведения, входящие в данную переключательную функцию. Очевидно, что если какое-либо элементарное произведение входит в данную переключательную функцию, то при добавлении к нему любых сомножителей новое произведение также всегда будет входить в эту функцию, т.к. оно обращается в нуль вместе с исходным произведением.
Теорема 2.1. Любая переключательная функция равняется дизъюнкции всех своих простых импликант.
Для доказательства рассмотрим наборы, на которых заданная переключательная функция равна нулю. Так как все простые импликанты входят в переключательную функцию по определению, то они будут также равны нулю на этих наборах, а, следовательно, будут равны нулю и их дизъюнкции.
Рассмотрим далее наборы, на которых переключательная функция равна единице. Для каждого такого набора найдется хотя бы одна импликанта, равная на этом наборе единице. Действительно, простые импликанты выбираются среди все элементарных произведений, входящих в переключательную функцию. В число этих произведений входят и все конституенты единицы данной функции. Но любая простая импликанта является собственной частью некоторых конституент единицы (или совпадает с одной из них). Например, при трех переменных элементарное произведение х1х2 будет собственной частью конституент х1х2х3 и x1 x2 x3 , а элемен-
тарное произведение х2 – собственной частью конституент x1 x2 x3 , x1 x2 x3 ,
x1 x2 x3 .
Если некоторые конституенты единицы не входят в набор всех простых импликант, то это означает, что они заменяются более короткими элементарными произведениями – простыми импликантами. Простая импликанта равняется единице на тех же наборах, на которых равны единице входящие в нее конституенты. Следовательно, среди всех простых им-
26
пликант всегда найдутся такие, которые вместе с заданной функцией обращаются на данном наборе в единицу.
Таким образом, дизъюнкция всех простых импликант накрывает все нули и все единицы заданной функции и, следовательно, совпадают с этой функцией.
2.2. Теорема Квайна
Теорема 2.2.1 (теорема Квайна). Если в совершенной дизъюнктивной нормальной форме переключательной функции выполнить все операции неполного склеивания, а затем все операции поглощения, то в результате будет получена сокращенная дизъюнктивная нормаль-
ная форма этой функции, или дизъюнкция всех ее простых импликант.
Следует обратить внимание на требование теоремы "выполнить все операции неполного склеивания" и "все операции поглощения". Кроме того, теорема дает определение сокращенной дизъюнктивной нормальной формы переключательной функции – это дизъюнкция всех ее простых импликант.
Точно так же теорема Квайна формулируется применительно к конъюнктивным формам переключательных функций.
Важность этой теоремы обусловлена тем, что она определяет конструктивное правило нахождения всех простых импликант переключательной функции.
Доказать теорему можно путем следующих рассуждений. Прежде всего покажем, что в результате проведения операций неполного склеивания получим все простые импликанты. Для этого рассмотрим операцию, обратную операции склеивания, называемую операцией развертывания.
Операция развертывания заключается в умножении некоторых импликант на выражение типа x x = 1, что, естественно, не меняет их значений. С помощью операции развертывания любую простую импликанту можно представить в виде дизъюнкции конституент единицы.
Пусть, например, xy – простая импликанта переключательной функции
четырех аргументов: x, y, z, u. Тогда, применяя дважды операцию развертывания, получаем
xy = xy(z z) = xyz xyz = xyz(u u ) xyz(u u ) = xyzu xyzu xyzu xyzu
.
Сокращенная дизъюнктивная нормальная форма содержит все простые импликанты заданной функции. Применяя к каждой импликанте опера-
27
цию развертывания, получаем, очевидно, все конституенты единицы этой функции.
При развертывании различные импликанты могут, вообще говоря, образовать одну и ту же конституенту. Поэтому после проведения операций развертывания полученное выражение может содержать несколько одинаковых конституент. Если дизъюнкцию одинаковых конституент заменить одной конституентой, то получим совершенную дизъюнктивную нормальную форму заданной переключательной функции.
Так как операция развертывания является обратной по отношению к операции склеивания, то, применяя операции склеивания к совершенной дизъюнктивной нормальной форме, можно получить любую простую импликанту. Для того чтобы получить все простые импликанты, необходимо провести операции неполного склеивания. Это связано с тем, что одно и то же логическое слагаемое дизъюнктивной формы может склеиваться с несколькими другими, образуя при этом различные импликанты. Поэтому при проведении операций склеивания каждое логическое слагаемое следует оставлять в выражении для использования его при других склеиваниях.
Полученная после проведения всех операции неполного склеивания дизъюнктивная форма будет содержать кроме всех простых импликант и другие логические слагаемые (в том числе все конституенты единицы переключательной функции). Если теперь провести все операции поглощения, то в дизъюнктивной форме останутся только простые импликанты. Покажем это.
Пусть, например, после проведения всех операций склеивания дизъюнктивная форма будет содержать слагаемое q, не являющееся простой импликантой. Тогда оно должно входить в данную функцию (q f), так как в противном случае полученной выражение не равняется исходному. Но по предположению q не является простой импликантой и входит в функций f; следовательно, в эту функцию входит какая-то его часть p, которая будет простой импликантой. Тогда q = q1p и слагаемое q будет поглощаться простой импликантой p:
p q=p q1 p=p .
Это и доказывает теорему Квайна.
Подчеркнем, что в соответствии с теоремой Квайна преобразование
нужно начинать, исходя из совершенной дизъюнктивной нормальной формы. Поэтому если функция задана в произвольной форме, то ее следует преобразовать в совершенную дизъюнктивную нормальную форму и только затем проводить операции склеивания и поглощения. При задании функции в произвольной дизъюнктивной нормальной форме для получения совершенной формы достаточно применить операции развертывания.
28

Практически сокращенную дизъюнктивную нормальную форму удобно находить в такой последовательности.
Провести в совершенной дизъюнктивной нормальной форме функции f(x1, x2, …, xn) все возможные операции склеивания конституент единицы. В результате этого образуются произведения, содержание (n-1) букв. Заметим, что конституенты единицы в дальнейшем не будут склеиваться ни с одним вновь полученным логическим слагаемым, так как склеиваться могут только произведения с одинаковым количеством букв. Потому можно сразу же провести операции поглощения, а затем выполнить все возможные склеивания слагаемых, состоящих из (n-1) букв. После этого провести поглощения слагаемых с (n-1) буквой и вновь выполнить операции склеивания слагаемых с числом букв, равным (n-2), и т.д.
Приведем несколько примеров получения сокращенных дизъюнктивных нормальных форм переключательных функций методом Квайна.
2.3. Метод импликантных матриц
Этот метод позволяет достаточно просто осуществлять переход от сокращенной формы переключательной функции к тупиковым и минимальным формам. Рассмотрим пример. Требуется найти минимальные дизъюнктивные нормальные формы переключательной функции, совершенная форма которой определяется выражением
f (x1 , x2 , x3 , x4 ) = x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 .
Построим для этой функции импликантную матрицу, представляющую собой таблицу, в вертикальные и горизонтальные входы которой записываются все конституенты единицы и все простые импликанты заданной функции соответственно (табл. 3.8).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.3.1. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
Импликантная матрица |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Конституенты единицы |
|
||||||||||||||||||||||
|
Простые |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
импли- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 x3 x4 |
|
|
|
|
|
x3 x4 |
x1 |
|
x3 x4 |
x1 |
|
|
|
x4 |
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x1 |
|
|
x1 |
|
x2 |
x2 |
x2 |
x3 |
x2 |
x3 |
x4 |
x1 |
x2 |
x3 |
x4 |
|
|||||||||||||||||||||
|
|
|
|
канты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 x4 |
|
|
X |
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x3 x4 |
|
|
|
|
|
|
|
|
X |
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x1 |
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
29
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
X |
X |
|
|
x2 |
|
x3 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
X |
|
x2 |
x3 |
x4 |
|
|
|
|
|
||||||||
Для каждой импликанты найдем конституенты единицы, которые ею поглощаются, т. е. те конституенты, собственной частью которых является данная импликанта. Например, импликанта x1 x3 x4 поглощает конститу-
енты x1 x2 x3 x4 и x1 x2 x3 x4 , импликанта x2 x3 x4 — конституенты x1 x2 x3 x4 и x1 x2 x3 x4 и т. д. Клетки импликантной матрицы, образованные пересечени-
ем строк с импликантами и колонок с поглощаемыми ими конституентами, отметим какими-либо символами..
Чтобы получить минимальную дизъюнктивную нормальную форму заданной функции, достаточно найти минимальное число импликант, которые совместно накрывают крестиками все колонки импликантной матрицы.
Из табл. 2.3.1 следует, что в минимальную форму обязательно должны войти импликанты x2 x3 x4 и x2 x3 x4 , так как только они накрывают крестиками первую и шестую колонки импликантной матрицы.
Кроме того, имлликанта x2 x3 x4 накрывает вторую, а импликанта x2 x3 x4 —
пятую колонки. Поэтому остается накрыть только третью и четвертую колонки. Для этого можно выбрать пары импликант: x2 x3 x4 и x1 x2 x4 ; x1 x2 x4 и
x1 x2 x3 или одну импликанту x1 x2 x4 . Если выбрать указанные выше пары импликант, то импликанты x2 x3 x4 и x1 x2 x3 оказываются лишними, так как импликанта x1 x2 x4 одна накрывает третью и четвертую колонки таблицы. Таким образом, выбрав импликанту x1 x2 x4 , получим минимальную дизъюнктивную нормальную форму заданной функции.
f (x1 , x2 , x3 , x4 ) = x1 x3 x4 x1 x2 x4 x2 x3 x4 ,
которая совпадает с первой тупиковой формой. Еслидополнительно к
x2 x3 x4 и x2 x3 x4 выбрать импликанты x2 x3 x4 и x1 x2 x3 , то лишних импликант не оказывается, а полученное выражение
f (x1 , x2 , x3 , x4 ) = x1 x3 x4 x2 x3 x4 x2 x3 x4 x1 x2 x3 ,
является второй тупиковой формой заданной функции.
Пример. Найти минимальные формы переключательной функции
30

f (x1 , x2 , x3 ) = |
x1 |
x2 x3 |
x1 |
|
x2 |
x3 x1 x2 x3 x1 x2 |
x3 |
x1 |
x2 |
|
x3 |
|
x1 |
|
x2 |
|
x3 |
. |
(2.3.1) |
Проводя все операции склеивания и поглощения, получим сокращенную дизъюнктивную нормальную форму:
1* −2* = |
|
|
|
|
x |
(по x |
), |
||||
x |
|||||||||||
|
|
1 |
3 |
2 |
|
|
|||||
1 −3* = x2 x3 |
(по x1), |
|
|||||||||
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 −6 = x1 x2 |
(по x3 ), |
||||||||||
3 −4* = x1x2 |
|
|
|
||||||||
(по x3 ), |
|||||||||||
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4 −5 = x1 x3 |
(по x2 ), |
||||||||||
5 −6 = |
|
|
|
|
|
|
|
(по x ); |
|
||
x |
2 |
x |
3 |
|
|||||||
|
|
|
|
|
|
1 |
|
|
|||
f (x1 , x2 , x3 ) = x1 x3 x2 x3 x1 x2 x1 x2 x1 x3 x2 x3 .
(2.3.2)
(2.3.3)
Составим импликаитную матрицу (табл. 2.3.2), выписав из выражения (2.3.1) все конституенты единицы, а из выражения (2.3.3) - все простые импликанты. При заполнении импликантной матрицы удобно пользоваться формой записи (2.3.2): следует поставить крестики в тех колонках, номера которых совпадают с числами, стоящими в левой части формы
(2.3.2).
Таблица 2.3.2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Импликантная матрица |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Конституенты единицы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Простые |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
импли- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
канты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|
x |
|
x1 x2 x4 |
x |
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
3 |
|
|
x |
1 |
|
x |
2 |
3 |
2 |
x |
3 |
|
|
x |
2 |
x |
3 |
x |
x |
2 |
x |
3 |
|
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
x4 |
|
X |
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
x2 x3 |
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
||||
|
x1 |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
x1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
X |
|
|
|
||||||
|
x2 |
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Для импликанты |
|
x4 |
крестиками отмечаются первая и вторая колонки; |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
x1 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
для x2 x3 — первая и третья и т. д. Заметим, что каждая колонка табл. 2.3.2
31
отмечена двумя крестиками. Поэтому из выражения (2.3.3) можно исключить любую импликанту. Минимальное количество импликант, накрывающих крестиками все колонки, равно трем:
x1 x3 накрывает первую и вторую колонки, x1 x2 накрывает третью и четвертую колонки, x2 x3 накрывает пятую и шестую колонки.
Поэтому минимальная дизъюнктивная нормальная форма заданной функции имеет вид
f (x1 , x2 , x3 ) = x1 x3 x1 x2 x2 x3 .
Можно накрыть все колонки табл. 3.9 и другими импликантами: x2 x3 накрывает первую и третью колонки,
x1 x2 накрывает вторую и шестую колонки, x1 x3 накрывает четвертую и пятую колонки.
Таким образом, данная функция имеет вторую минимальную форму
f (x1 , x2 , x3 ) = x2 x3 x1 x2 x1 x3 .
Переключательная функция f (x1 , x2 , x3 ) имеет несколько других тупико-
вых форм, которые, однако, не являются минимальными. Например, тупиковыми будут следующие формы:
f (x1 , x2 , x3 ) = x1 x3 x1 x2 x1 x2 x1 x3 ;
f (x1 , x2 , x3 ) = x2 x3 x1 x2 x1 x2 x2 x3 .
На основании изложенного сформулируем алгоритм получения минимальных дизъюнктивных нормальных форм переключательной функции.
1.Переключательную функцию представляют в совершенной дизъюнктивной нормальной форме. При этом, если функция задана таблицей, то ее следует записать «по единицам»; если же функция задана в произвольной аналитической форме, то совершенную дизъюнктивную нормальную форму можно получить, применяя операции развертывания, правила де Моргана и другие формулы булевой алгебры.
2.В полученной совершенной дизъюнктивной нормальной форме прово-
дят все операции неполного склеивания и поглощения. В результате этого получается сокращенная дизъюнктивная нормальная форма заданной функции.
3.Находят минимальные дизъюнктивные нормальные формы по импликантной матрице. Если количество импликант в сокращенной дизъюнк-
32

тивной нормальной форме невелико, то можно найти тупиковые формы методом испытания импликант и выбрать среди них минимальные. Заметим, что в ряде случаев минимальная дизъюнктивная форма совпадает с сокращенной. Например, сокращенная дизъюнктивная нормальная форма любой переключательной функции двух аргументов совпадает с минимальной формой. Точно так же импликантные матрицы применяются для получения тупиковых и минимальных конъюнктивных нормальных форм переключательных функций.
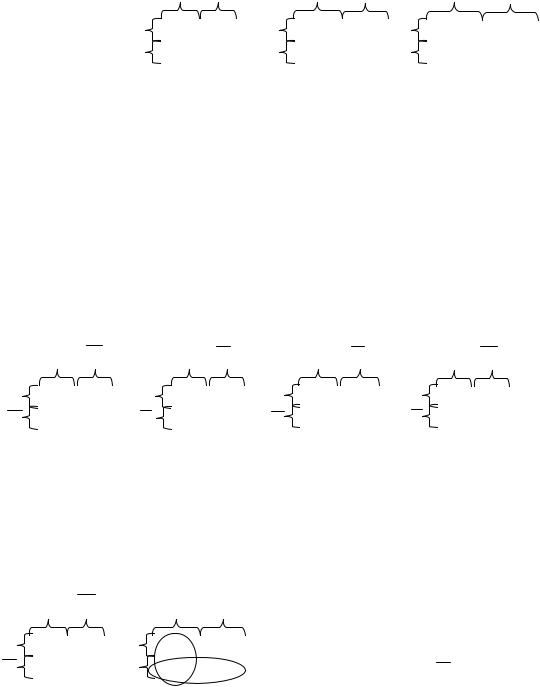
2.4. Метод испытания импликант
Этот метод удобно использовать тогда, когда число импликант, входящих в сокращенную форму функции невелико.
Отметим следующее свойство произвольной, в частности, сокращенной дизъюнктивной нормальной формы переключательной функции импликант:
- если из этой формы исключить одну или несколько импликант, то полученное после этого выражение будет обращаться в нуль на тех же наборах, что и исходное выражение.
Это связано с тем, что дизъюнктивная форма обращается в нуль только в том случае, когда все ее логические слагаемые равны нулю. Однако, при исключении импликанты может оказаться, что на тех наборах, на которых исключенная импликанта равнялась единице (а следовательно, вместе с ней и вся дизъюнкция равнялась единице ввиду соотношения 1 х1=1), оставшееся выражение не будет равно единице. Если же проверкой установить, что при исключении импликанты полученное выражение равно единице на этих наборах, то можно утверждать, что все нули и все единицы обоих выражений совпадают и, следовательно, исключенная импликанта является лишней.
Таким образом, чтобы испытать некоторую импликанту, ее следует исключить из сокращенной дизъюнктивной нормальной формы и подставить в оставшееся выражение такие значения переменных, которые обращают исключенную импликанту в единицу. Если при этом оставшееся выражение будет тождественно равно единице, то испытываемая импликанта является лишней.
Применение этого правила связано с некоторыми особенностями, которые можно рассмотреть на примерах.
Пример 1. Найти тупиковые формы переключательной функции, заданной в сокращенной дизъюнктивной нормальной форме:
f (x1 , x2 , x3 ) = x1 x2 x1 x3 x2 x3 .
33
1. Испытываем импликанту x1 x 2 . Подставляем в x1 x3 x2 x3 значения х1 = 0 и х2 = 0, т.к. при этом x1 x2 = 0 0 =1 :
0 x3 0 x3 = x3
Следовательно, импликанту x1 x2 исключать нельзя, т.к. оставшееся выражение не равно тождественно единице.
2.Импликанту х1х3 исключать также нельзя, т.к. при х1= 1 и х3 = 1
1 x2 x2 1 = 0 x2 x2 1 = x2
3.Для импликанты x2 x3 :
x1 0 x1 1 = x1 1 x1 1 = x1 x1 =1
Полученное выражение тождественно равно единице, поэтому импликанту x2 x3 можно исключить, т.к. она является лишней.
Пример 2. Упростить переключательную функцию.
f (x1 , x2 , x3 , x4 ) = x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 .
На основе теоремы Квайна получим
1÷2 → x1 x3 x4 2÷3 → x2 x3 x4
3÷4 → x1 x2 x4
4÷5 → x1 x2 x3 5÷6 → x2 x3 x4
Тогда сокращенная ДНФ имеет вид
f (x1 , x2 , x3 , x4 ) = x1 x3 x4 x2 x3 x4 x1 x2 x4 x1 x2 x3 x2 x3 x4
|
|
|
|
|
|
|
(2.4.1) |
|
|
|
|
|
|
|
|
|
||
Найдем тупиковые формы. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1. Для |
|
x3 x4 : х1 = 0, |
|
х3 = 1, |
х4 = 1: |
|||||||||||||
x1 |
||||||||||||||||||
|
|
|
|
|
|
1 1 0 |
|
1 0 x2 |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
x2 |
x2 |
1 |
x2 |
1 |
1 |
x2 |
|||||||
т.е. первую импликанту исключать нельзя. |
||||||||||||||||||
2. Для |
|
x3 x4 : х2 = 0, |
х3 = 1, |
х4 = 1. |
||||||||||||||
x2 |
||||||||||||||||||
x1 1 1 x1 0 1 x1 0 1 0 1 1 = x1 x1 =1,
т.е. импликанта x2 x3 x4 является лишней.
34

3. Проверяем третью импликанту x1 x2 x4 ; при этом вторую импликанту, которая оказалась лишней, вновь возвращаем в исследуемое выражение. Тогда, подставляя в выражение
x1 x3 x4 x2 x3 x4 x1 x2 x3 x2 x3 x4
значения х1 = 1, х2 = 0, х4 = 1, получим
1 x3 1 0 x3 1 1 0 x3 0 x3 1 = x3 x3 =1.
Следовательно, импликанта x1 x2 x4 также лишняя и может быть исключена.
4. Аналогично можно показать, что и импликанту x1 x2 x3 также может быть исключена.
Таким образом выражение (2.4.1) имеет три лишние импликанты x2 x3 x4
x1 x2 x4 и x1 x2 x3 .
Однако исключать одновременно все лишние импликанты нельзя без дополнительной проверки. Вначале следует исключить одну импликанту полученного выражения. Исключим из выражения (24.1. импликанту
x2 x3 x4 , получим
f (x1 , x2 , x3 , x4 ) = x1 x3 x4 x1 x2 x4 x1 x2 x3 x2 x3 x4
Вновь проверяем наличие лишних импликант, проверяя только те, которые были лишними при первой проверке, т.е. импликанты x1 x2 x4 и x1 x2 x3 . Подставляя в выражение
x1 x3 x4 x1 x2 x3 x2 x3 x4
значения х1 = 1, х2 = 0, х4 = 1 получаем
1 x3 1 1 0 x3 0 x3 1 = x3 .
Следовательно, импликанту x1 x2 x4 исключать нельзя, хотя при первой проверке, т.е. при наличии x2 x3 x4 (тоже лишней), она была лишней.
Поэтому если в некотором выражении имеется несколько лишних импликант, то исключение двух и более импликант одновременно без дополнительной проверки недопустимо.
2.5. Минимизация переключательных функций с помощью диаграмм Вейча
Диаграммы Вейча позволяют упростить поиск склеивающихся конституент. Диаграмма Вейча – это специальная таблица, определяющая значения
35
переключательной функции на каждом наборе аргументов. Каждой клетке диаграммы соответствует определенный набор значений аргументов – рис. 2.5.1.б.
x2 |
1 |
0 |
|
x2 |
x2 |
|
x2 |
x2 |
|
x2 |
x2 |
|
х1 |
|
|
х1 |
|
|
|
х1 |
|
|
х1 |
|
|
1 |
|
|
1,1 |
|
1,0 |
х1x2 |
х1x2 |
х1 x2 |
х1 x2 |
|||
0 |
|
|
х1 |
0,1 |
|
0,0 |
х1 |
х1x2 |
х1x2 |
х1 |
х1 x2 |
х1 x2 |
(а) |
|
|
(б) |
|
|
(в) |
|
|
(г) |
|
||
Рис. 2.5.1. Диаграмма Вейча для функции двух переменных. Склеивающиеся между собой конституенты единицы или нуля в диа-
граммах Вейча для функций двух аргументов расположены в соседних клетках (рис. 2.5.1.в, г).
Чтобы представить переключательную функцию диаграммой Вейча следует записать единицы в клетки, соответствующие наборам, на которых функция равна единице, и нули – в остальные клетки.
В диаграмме Вейча для переключательной функции двух аргументов лю-
бая пара единиц, расположенных в соседних клетках, выражается одной буквой.
|
|
x2 |
|
x2 |
|
|
|
x2 |
|
x2 |
|
x2 |
|
x2 |
|
|
x2 |
x2 |
||||||||||
х1 |
|
|
|
|
|
|
х1 |
|
|
|
|
|
х1 |
|
|
|
|
|
|
|
х1 |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
1 |
|
|
0 |
0 |
0 |
|
0 |
1 |
|
||||||||||||||
х1 |
|
0 |
|
|
0 |
|
х1 |
|
1 |
|
|
0 |
х1 |
1 |
1 |
|
|
|
|
х1 |
|
0 |
1 |
|
|
|||
f2(х1; x2) = x1 |
f5(х1; x2) = x2 |
f12 = х1 |
|
|
|
|
|
|
f10 = х2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Это обстоятельство используют для получения минимальных ДНФ и |
||||||||||||||||||||||||||||
КНФ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f13(х1; x2) = |
|||||
Рассмотрим диаграммы Вейча переключательной функции |
|
|||||||||||||||||||||||||||
= х1→ x2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
x2 |
|
|
|
x2 |
|
x2 |
Пара единиц во второй строке со- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ответствует х1 |
|
пара единиц в |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, а |
||||||||||||||
х1 |
1 |
|
0 |
|
х1 |
|
х1x2 |
|
|
|
первой колонке – x2. |
|
|
|
|
|||||||||||||
х1 |
1 |
|
1 |
|
х1 |
|
х1x2 |
|
х1x2 |
|
|
|
f13(х1; x2) = |
х1 x2. |
||||||||||||||
Это выражение, являющееся минимальной формой функции f13(x1;x2) получено путем склеивания конституент единиц, обведенных овалами.
Для 3-х переменных
Эти диаграммы следует представлять в виде36 цилиндра, образованного соедине-
|
|
x2 |
|
|
x2 |
x1 |
x1x2x3 |
x1x2 x3 |
x1x2 x3 |
x1x2 x3 |
|
x1 |
x1x2 x3 |
x1x2 x3 |
x1x2 x3 |
x1x2 x3 |
|
|
x3 |
|
|
x3 |
x3 |
|
|
|
x2 |
|
x2 |
x1 |
x1 x2 x3 |
x1 x2 x3 x1 x2 x3 x1 x2 x3 |
|||
x1 |
x1 x2 x3 |
x1 x2 x3 x1 x2 x3 x1 x2 x3 |
|||
|
x3 |
|
|
x3 |
x3 |
|
|
x2 |
|
|
x2 |
x1 |
110 |
|
111 |
101 |
100 |
x1 |
010 |
|
011 |
001 |
000 |
|
x3 |
|
|
x3 |
x3 |
Рассмотрим диаграммы Вейча переключательных функций, которые выражаются произведением двух переменных
|
|
x2 |
|
x2 |
|
|
x2 |
|
x2 |
|
|
x2 |
|
x2 |
x1 |
1 |
1 |
0 |
0 |
x1 |
0 |
0 |
0 |
0 |
x1 |
0 |
0 |
1 |
0 |
x1 |
0 |
0 |
0 |
0 |
x1 |
0 |
1 |
1 |
0 |
x1 |
0 |
0 |
1 |
0 |
|
x3 |
|
x3 |
x3 |
|
x3 |
|
x3 |
x3 |
|
x3 |
|
x3 |
x3 |
|
|
x1 x2 |
|
|
|
x1 x3 |
|
|
|
x2 x3 |
|
|||
|
|
x2 |
|
x2 |
|
|
x2 |
|
x2 |
|
|
x2 |
|
x2 |
x1 |
0 |
0 |
0 |
0 |
x1 |
1 |
0 |
0 |
1 |
x1 |
0 |
0 |
1 |
1 |
x1 |
1 |
0 |
0 |
1 |
x1 |
0 |
0 |
0 |
0 |
x1 |
0 |
0 |
0 |
0 |
|
x3 |
|
x3 |
x3 |
|
x3 |
x3 |
x3 |
|
x3 |
|
x3 |
x3 |
|
|
|
x1 x3 |
|
|
|
|
x1 x3 |
|
|
|
x1 x2 |
|
||
Четыре единицы, расположенные в соседних клетках, выражаются одной буквой.
|
|
x2 |
|
x2 |
|
|
x2 |
|
x2 |
|
|
x2 |
|
x2 |
x1 |
0 |
1 |
1 |
0 |
x1 |
0 |
0 |
0 |
0 |
x1 |
1 |
0 |
0 |
1 |
x1 |
0 |
1 |
1 |
0 |
x1 |
1 |
1 |
1 |
1 |
x1 |
1 |
0 |
0 |
1 |
37
|
x3 |
|
|
|
|
|
x3 |
|
|
|
x3 |
|
|||
|
|
|
|
||||||||||||
x3 |
x3 |
x3 |
|||||||||||||
x3 |
x3 |
x3 |
|||||||||||||
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
x3 |
|
|||
Чтобы построить диаграмму Вейча функции, заданной в СДНФ, нужно записать единицы в клетки диаграммы, которые соответствуют конституентам единицы данной функции.
Если функция задана в СКНФ, следует записать нули в клетки диаграммы, которые соответствуют конституентам нуля, входящим в данную функцию, а в остальных клетках записать единицы.
Отыскание минимальной ДНФ сводится к определению варианта, при котором все единицы диаграммы Вейча данной функции накрываются наименьшим числом наиболее коротких произведений.
Пример.
f(x1, x2, x3) = x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 .
f(x1, x2, x3) = x3 x1 x2 x1 x2 .
|
x2 |
x2 |
|
Четыре единицы, находящиеся в первой и |
|
|
|
последней колонках, можно накрыть перемен- |
|||
x1 |
1 |
0 |
1 |
1 |
ной x3 , а две остальные объединить с единица- |
x1 |
1 |
1 |
0 |
1 |
ми, расположенными в левой нижней и правой |
x3 |
x3 |
|
x3 |
верхней клетках диаграммы (склеивание по x3). |
|
Данная функция имеет единственную минимальную форму, так как при любом другом способе объединения единиц количество букв в ДНФ увеличивается.
Пример. Найти минимальные ДНФ и КНФ функции
f(x1, x2, x3) = x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 .
|
|
x2 |
|
x2 |
|
x2 |
|
|
x2 |
x1 |
1 |
1 |
1 |
0 |
x1 |
1 |
1 |
1 |
0 |
x1 |
0 |
0 |
1 |
1 |
x1 |
0 |
0 |
1 |
1 |
|
x3 |
|
x3 |
x3 |
|
x3 |
|
x3 |
x3 |
f(x1, x2, x3) = x1 x2 x1 x3 x1 x2 |
|
f(x1, x2, x3) = x1 x2 x2 x3 x1 x2 |
|||||||
Для получения минимальной КНФ следует объединить нули переключательной функции: две конституенты нуля соответствуют клеткам, объединенным пунктиром, склеиваются по x3 и представляются импликантой
38
x1 x2 , а оставшийся нуль – конституентой x1 x2 x3. Поэтому минимальная КНФ будет иметь вид:
f(x1, x2, x3) = (x1 x2 )( x1 x2 x3).
Минимальная КНФ имеет меньше букв, чем минимальная ДНФ.
Пример. Найти минимальную ДНФ.
f(x1, x2, x3) = x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 .
|
x2 |
|
x2 |
|
Единственная минимальная ДНФ имеет |
|
x1 |
1 |
0 |
0 |
1 |
вид |
x1 x3 x2 x3 x1 x2 x3 |
|
|
|||||
x1 |
1 |
0 |
1 |
0 |
|
|
x3 |
x3 |
|
x3 |
|
|
|
Пример. Найти минимальную ДНФ.
f(x1, x2, x3) = x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 .
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
f(x1, x2, x3) = x2 x3 x1 x3 x1 x2; |
|||||||||
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x1, x2, x3) = x1 x3 x1 x2 x2 x3; |
|||||||||
1 |
|
0 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
При других способах объединения консти- |
||||||||||||
|
|
x3 |
|
x3 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
туент число логических слагаемых в ДНФ |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
будет больше трех. |
||||||||||
Пример. Найти минимальную ДНФ функции |
|||||||||||||||||||||||||||||||
f(x1, x2, x3) = x1 x2 |
|
|
|
x2 x3 x1 |
|
x3 |
|
|
|
|
|
|
. |
||||||||||||||||||
x3 |
x1 |
x2 |
x1 |
x2 |
x3 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
В диаграмме Вейча данной функции нет |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
ни одной пары единиц, расположенных |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в соседних клетках, и поэтому заданная |
||||||
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
СДНФ совпадает с минимальной. |
|||||||||||||||||
|
|
1 |
|
0 |
|
1 |
|
|
|
0 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
0 |
|
1 |
|
|
0 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
x3 |
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Диаграмма Вейча для функции четырех аргументов представляет собой квадрат, разделенный на 16 клеток.
39
x2 x2
x3
x1
x3
x1
x3
x4 |
x4 |
x4 |
Одной букве соответствует восемь единиц, расположенных в соседних клетках; произведению, включающему две переменные соответствуют четыре соседние единицы; произведению трех переменных – две и произведению четырех переменных
– одна единица.
Первую и последнюю колонки диаграммы, а также верхнюю и нижнюю строки следует считать соседними. Поэтому диаграмму Вейча для функций четырех аргументов следует представлять нанесенной на поверхность тора.
Пример.
f (x1 x2 x3 x4 ) = x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4
|
|
|
|
|
x2 |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
f (x1 x2 x3 ) = x3 |
|
x1 x2 |
|
|
|
|
|
x3 |
|
x2 |
|
x4 – |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
x4 |
x1 |
|
x2 |
x1 |
x3 |
||||||
x1 |
1 |
|
|
0 |
0 |
|
0 |
|
x3 |
|
- это минимальная ДНФ. |
|||||||||||||||||
1 |
|
|
0 |
0 |
|
1 |
x3 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
|
|
0 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
0 |
|
|
1 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 x4 x4
Диаграмма Вейча для функции пяти аргументов имеет следующий вид:
|
x2 |
x2 |
x5 |
x5 |
x5 |
40

x1 x3
x3
x1
x3
x4 |
x4 |
x4 |
x4 |
x4 |
Одной букве в этом случае соответствуют шестнадцать единиц, расположенных в смежных клетках; произведение двух букв – восемь единиц, трех букв – четыре, четырех – две и пяти – одна единица.
Следует помнить, что для букв x3 , x4, x4 и x5 "соседние" клетки оказы-
ваются разнесенными.
Аналогично строится диаграмма Вейча и для переключательных функций большего числа аргументов. Однако с увеличением числа аргументов работа с диаграммами затрудняется, т.к. теряется геометрический смысл "соседних" клеток.
2.6. Второй метод получения минимальных КНФ Этот метод полностью опирается на преобразования дизъюнктивных
форм переключательных функций. Алгоритм заключается в следующем.
1.Записывают дизъюнкцию всех конституент единицы, которые не входят в СДНФ заданной функции.
Если функция задана таблицей, то в эту форму войдут конституенты единицы, соответствующие наборам аргументов, на которых функция равна нулю. Если функция задана аналитически, то вначале находят ее совершенную ДНФ, а затем записывают дизъюнкцию всех конституент, которые не вошли в эту функцию. Можно показать, что полученная таким образом форма будет совершенной дизъюнктивной нормальной формой заданной функции, взятой с отрицанием.
2.Находят минимальные ДНФ по рассмотренным алгоритмам.
3.От полученных минимальных форм берут отрицания, и после преобразований по формулам де Моргана получают конъюнктивные формы, которые будут минимальными.
Для обоснования приведенного алгоритма получения минимальной КНФ достаточно доказать два положения.
1.Дизъюнкция всех конституент единицы, не входящих в совершенную дизъюнктивную нормальную форму данной функции f(x1, x2, …, xn) явля-
ется отрицанием данной функции f (x1, x2 ,..., xn ) .
41

2. Преобразования по формулам де Моргана минимальной дизъюнк-
тивной нормальной формы функции f (x1, x2 ,..., xn ) приводит к получе-
нию минимальной конъюнктивной нормальной формы функции f(x1, x2,
…, xn).
1. Прежде всего заметим, что дизъюнкция всех конституент единицы тождественно равна единице. Действительно, для любого набора аргументов в такой дизъюнкции найдется конституента, равная на этом наборе единице. Но если одно логическое слагаемое ДНФ равно единице, то равна единице и вся дизъюнктивная форма. Поэтому справедливы такие, например, соотношения
x1 x2 x1 x2 x1 x2 x1 x2 =1
x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 =1
В общем виде:
K0 K1 ... K2n −1 =1, |
(*) |
где n – число аргументов. |
|
Рассмотрим некоторую ПФ, заданную в СДНФ: |
|
f (x1, x2 ,..., xn ) = K j1 K j2 ... K jm , |
(**) |
где m – число наборов, на которых ПФ равна единице.
Обозначим конституенты единицы, не входящие в последнее выражение, через Ki1 , Ki2 ,..., Kip , где p = 2n – m – число наборов, на которых функция
равна нулю. Тогда на основании соотношения (*)
K j1 K j2 ...K jm Ki1 Ki2 ... Kip =1
Учитывая (**), получим
f (x1, x2 ,..., xn ) Ki1 Ki2 ... Kip =1
Сравнивая последнее соотношение с тождеством х1 x1 = 1, которое можно записать в форме
f (x1, x2 ,..., xn ) f (x1, x2 ,..., xn ) =1,
получим
f (x1, x2 ,..., xn ) = Ki1 Ki2 ... Kip ,
что и требовалось доказать.
Преобразования по формулам де Моргана не изменяют число букв в выражении для ПФ. Поэтому, если взять отрицание от минимальной ДНФ
функции f (x1, x2 ,..., xn ) , то полученная после преобразования по форму-
лам де Моргана конъюнктивная форма также будет минимальной, но уже для функции f (x1, x2 ,..., xn ) .
Если предположить, что эта форма не является минимальной, то существует другая конъюнктивная форма, содержащая меньшее число букв. То-
42

гда, взяв от нее отрицание и применив формулы де Моргана, получим дизъюнктивную форму с меньшим числом букв, чем в минимальной. Это противоречит определению минимальной формы и, следовательно, предположение о том, что полученная конъюнктивная форма не является минимальной, не верно.
Пример 1. Найти минимальную конъюнктивную форму ПФ, заданной таблицей.
Номер |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1. Запишем дизъюнкцию кон- |
|
набора |
|
|
|
|
|
|
|
|
ституент единицы, которые со- |
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
||
x1 |
ответствуют наборам, на ко- |
|||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
торых функция равна нулю. |
|
x2 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
||
|
||||||||||
x3 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
f(x1, x2, x3) |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
f (x1 , x2 , x3 ) = x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 .
2. Выполним операции склеивания и поглощения, после чего получим сокращенную ДНФ функции f (x1 , x2 , x3 ) :
f(x1 , x2 , x3 ) = x1 x2 x2 x3 x1 x3 .
3.Испытывая импликанты, обнаружим, что вторую импликанту можно
исключить (при x2 = 1, x3 = 0, выражение x1 x2 x1 x3 ≡ 1), т.е. минимальная ДНФ функции f (x1 , x2 , x3 ) имеет вид
f (x1 , x2 , x3 ) = x1 x2 x1 x3 .
Использовав формулу де Моргана, получим минимальную КНФ заданной функции
f (x1 , x2 , x3 ) = x1 x2 x1 x3 = (x1 x2 )(x1 x3 ) .
Пример 2. Найти минимальную конъюнктивную нормальную форму функции
f (x1 , x2 , x3 ) = x1 x3 x1 x2 x3 .
1. Находим СДНФ:
f (x1 , x2 , x3 ) = x1 (x2 x2 )x3 x1 x2 x3 = x1 x2 x3 x1 x x3 x1 x2 x3 .
2. Записав дизъюнкцию конституент единицы, не вошедших в предыдущее выражение, получим СДНФ функции f (x1 , x2 , x3 ) :
f (x1 , x2 , x3 ) = x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 .
3. Сокращенная ДНФ имеет вид:
f (x1 , x2 , x3 ) = x1 x3 x1 x2 x2 x3 x1 x3 .
43

4. Находим минимальные формы функции f (x1 , x2 , x3 ) .
Импли- |
|
|
|
|
|
|
|
|
Конституента |
|
|
|
|
||||||||||
канта |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x1 x2 |
x3 |
|
|
x1 x2 x3 |
|
|
x1 x2 x3 |
|
x1 x2 x3 |
x1x2 x3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
* |
|
* |
|
|
|
|
|
|
|
|
|
|||
|
x1 |
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
x2 |
|
|
|
|
* |
|
* |
|
|
|
|
|
||||||
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
x2 |
|
|
x3 |
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
* |
|||||
x1 |
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
* |
|||||
1)f (x1 , x2 , x3 ) = x1 x3 x2 x3 x1 x3 .
2)f (x1 , x2 , x3 ) = x1 x3 x1 x2 x1 x3 .
Воспользовавшись формулой де Моргана получим две минимальные КНФ:
1.f(x1, x2, x3) = (x1 x3)( x2 x3)( x1 x3).
2.f(x1, x2, x3) = (x1 x3)( x1 x2)( x1 x3).
2.7.Минимизация неполностью определенных переключательных
функций
В ЦВМ могут использоваться комбинационные схемы, закон функционирования которых определен неполностью. В таких схемах некоторые комбинации сигналов на ее входы не подаются и являются запрещенными. Для запрещенных входных комбинаций выходные сигналы не определены, т.е. могут принимать любые значения – нуль или единицу. Поэтому при синтезе схем с неполностью заданным законом функционирования можно произвольно задать значения выходных сигналов для запрещенных комбинаций входных сигналов; нормальная работа схемы при этом не нарушается. Поэтому выходным сигналам на запрещенных комбинациях придают такие значения, при которых можно построить наиболее простую схему.
Схемы с запрещенными комбинациями выходных сигналов описываются неполностью определенными переключательными функциями, т.е. функциями, значения которых определены не на всех наборах. Например, функция заданная таблицей и диаграммой Вейча
x1 |
0 |
0 |
0 |
0 |
1 |
x2 |
x2 |
1 |
|
||||||
|
|
|
|
|
|
x1 1 |
1 |
x1 B |
0 |
0 |
0 1 |
x3 |
x3 |
xB |
44 |
3B |

x2 |
0 |
0 |
1 |
1 |
0 |
1 |
x3 |
0 |
1 |
0 |
1 |
1 |
0 |
f(x1, x2, x3) |
1 |
0 |
0 |
0 |
1 |
1 |
определена только на шести наборах. Клетки, соответствующие наборам 1,0,0; 1,1,1 остаются пустыми.
Форма представления функции f(x1, x2, x3) существенно зависит от выбора ее значений на запрещенных наборах, Например, для заданной функции, выбирая ее запрещенные значения равными нулю, можно получить минимальную ДНФ в виде
f (x1 , x2 , x3 ) = x1 x2 x3 x1 x2 x3 x1 x2 x3
Если значения функции на запрещенных наборах принять равными единице, то форма представления упрощается
f (x1 , x2 , x3 ) = x1 x2 x3 .
Рассмотрим общую методику получения минимальных ДНФ неполностью определенных переключательных функций
Определение 2.7.1. Пусть переключательная функция f(x1, x2, …, xn) не определена на p наборах аргументов. Тогда полностью определенную функцию ϕ(x1, x2, …, xn) будем называть эквивалентной функции f(x1, x2, …, xn), если ее значения совпадают со значениями функции f(x1, x2, …, xn) на тех наборах, на которых эта функция f определена.
Существует 2p вариантов выбора значений функции на запрещенных наборах и, следовательно, 2р различных переключательных функций, эквивалентных функции f(x1, x2, …, xn). Поэтому задача минимизации неполностью определенной функции f(x1, x2, …, xn) сводится к отысканию такой эквивалентной функции ϕ(x1, x2, …, xn), которая имеет простейшую минимальную форму.
Введем эквивалентные функции ϕ0(x1, x2, …, xn) и ϕ1(x1, x2, …, xn), значения которых на всех запрещенных наборах функции f(x1, x2, …, xn) равны, соответственно, нулю и единице.
Теорема 2.7.1. Минимальная ДНФ неполностью определенной функции f(x1, x2, …, xn) совпадает с дизъюнкцией самых коротких импликант эквивалентной функции ϕ1(x1, x2, …, xn), которые совместно поглощают все конституенты единицы функции ϕ0(x1, x2, …, xn) и ни
одна из которых не является лишней.
Для доказательства теоремы рассмотрим СДНФ некоторой эквивалентной функции ϕi(x1, x2, …, xn). Конституенты единицы, входящие в эту форму, обязательно войдут и в СДНФ функции ϕ1(x1, x2, …, xn). Поэтому любая простая импликанта функции ϕi(x1, x2, …, xn) будет совпадать с импликантой функции ϕ1(x1, x2, …, xn) или будет поглощаться ею. Другими слова-
45

ми, среди импликант функции ϕ1(x1, x2, …, xn) всегда найдется такая, которая поглощает любую импликанту любой эквивалентной функции ϕi(x1, x2, …, xn). Следовательно, самыми короткими произведениями, накрывающими единицы функции f(x1, x2, …, xn), будут импликанты ϕ1(x1, x2, …, xn).
Среди всех ПФ, эквивалентных заданной, функция ϕ0(x1, x2, …, xn) имеет минимальное количество конституент единицы. Следовательно, и количество простых импликант [из набора импликант функции ϕ1(x1, x2, …, xn)], необходимых для поглощения конституент функции ϕ0(x1, x2, …, xn), будет минимальным. Если составить дизъюнкции наиболее коротких импликант функции ϕ0(x1, x2, …, xn), которые совместно накрывают все конституенты единицы функции ϕ0(x1, x2, …, xn), то получим, очевидно, минимальную форму представления функции f(x1, x2, …, xn).
Ввиду того, что для накрытия единиц функции ϕ0(x1, x2, …, xn) выбираются импликанты другой функции, дизъюнкция этих импликант не равняется функции ϕ0(x1, x2, …, xn). Однако, такая дизъюнкция обязательно равна одной из функций, эквивалентных функции f(x1, x2, …, xn). Пример. Найти минимальную дизъюнктивную нормальную форму ПФ, заданной таблицей.
x1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
x2 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
x3 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
x4 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
f(x1, x2, x3, x4) |
1 |
|
|
|
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
1 |
|
|
1 |
Полагая, что пустые клетки заполнены нулями, найдем СДНФ эквивалентной функции ϕ0(x1, x2, x3, x4):
ϕ0 (x1 , x2 , x3 , x4 ) = x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 .
СНДФ функции ϕ1(x1, x2, …, xn), полученная после заполнения пустых клеток таблицы единицами, будет
ϕ1 (x1 , x2 , x3 , x4 ) = x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4
x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 .
Выполнив операции склеивания и поглощения, получим сокращенную ДНФ функции ϕ1 (x1, x2, x3, x4), в которую войдут все ее простые импликанты:
ϕ1(x1, x2 , x3, x4 ) = x1x2 x1 x2 x1 x4 x2 x4 x1 x3x4 x2 x3x4
46

Составим импликантную матрицу, включив в нее конституенты единицы функции ϕ0(x1, x2, x3, x4) и импликанты функции ϕ1(x1, x2, x3, x4).
|
Импли- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Конституенты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
канты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x |
1 |
|
x |
2 |
|
x |
3 |
|
x |
4 |
|
|
x |
x |
2 |
x |
x |
4 |
|
|
x |
1 |
x |
2 |
|
x |
3 |
|
x |
4 |
|
x |
x |
2 |
|
x |
3 |
|
x |
4 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
x1 x2 x3 x4 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x1 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x2 |
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x1 |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
x2 |
|
|
|
|
|
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Импликанта x1x2 обязательно должна входить в мин ДНФ, т.к. только |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
она поглощает конституенту x1x2x3x4. |
Импликанты x1x2 |
|
|
|
совместно |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x3 |
x4 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
накрывают все конституенты, кроме |
|
|
x2 |
|
x4 ; |
последняя может быть на- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x1 |
x3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
крыта импликантами |
|
|
|
|
|
|
x4 |
|
или |
x2 |
|
x4 . |
|
|
Поэтому |
минимальные ДНФ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x1 |
|
x3 |
|
x3 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
функции f(x1, x2, x3, x4) будут:
f (x1 , x2 , x3 , x4 ) = x1 x2 x2 x4 x1 x3 x4 , f (x1 , x2 , x3 , x4 ) = x1 x2 x2 x4 x2 x3 x4 .
Пример. Найти минимальную ДНФ функции f(x1, x2, x3, x4), эквивалентая функция ϕ0(x1, x2, x3, x4) которой имеет вид:
ϕ0 (x1 , x2 , x3 , x4 ) = x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 ,
а комбинации x1 x2 x3 x4 , x1 x2 x3 x4 , x1 x2 x3 x4 , x1 x2 x3 x4 являются запрещенными.
Эквивалентную функцию ϕ1(x1, x2, …, xn) можно получить, добавив к СДНФ функции ϕ1(x1, x2, …, xn) запрещенные комбинации переменных:
ϕ1 (x1 , x2 , x3 , x4 ) = x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4
x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 .
Проведя операции склеивания и поглощения, найдем простые импликанты функции ϕ1(x1, x2, x3, x4); x1x2x3, x1x3x4, x1 x3 , x2 x4 . Импликантная матрица функции f(x1, x2, x3, x4) имеет вид.
Импли- Конституенты
47

канты |
x1 x2 x3 |
|
x1 |
|
|
|
x4 |
|
|
|
x3 x4 |
|
x2 |
|
|
|
|
|
|
|
|
|
|
x4 |
x2 |
|
x3 |
x1 |
x2 |
x1 |
x3 |
x4 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
x1 |
|
x2 |
|
x3 x4 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
x |
x |
|
x1 |
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
х |
х |
х |
|
|
x2 |
x4 |
||||||
x1x2x3 |
х |
|
|
|||||
|
|
|
||||||
|
|
|
|
|||||
x1x3x4 |
|
|
|
|||||
Функция f(x1, x2, x3, x4) имеет единственную минимальную ДНФ
f (x1 , x2 , x3 , x4 ) = x1 x3 x2 x4 x1 x2 x3 .
В нижней строке импликантной матрицы крестики отсутствуют и, следовательно, импликанта x1x3x4 не поглощает ни одну из конституент единицы функции ϕ0(x1, x2, x3, x4). Это связано с тем, что данная импликанта образовалась в результате склеивания конституент функции ϕ1(x1, x2, x3, x4), которые в функцию ϕ0(x1, x2, x3, x4) не входят.
Чтобы найти простейшее представление неполностью определенной ПФ, кроме минимальных дизъюнктивных форм следует получить минимальные конъюнктивные нормальные формы и выбрать из них ту, которая содержит наименьшее число букв.
Алгоритм получения минимальных конъюнктивных форм подобен рассмотренному алгоритму получения минимальной ДНФ и заключается в следующем.
Пусть задана неполностью определенная функция f(x1, x2, …, xn). Тогда для получения минимальной КНФ достаточно найти сокращенную КНФ эквивалентной функции ϕ0(x1, x2, …, xn), а функцию ϕ1(x1, x2, …, xn) записать в СКНФ. Затем следует составить ипликантную матрицу, включив в нее все конституенты нуля функции ϕ1(x1, x2, …, xn) и все члены сокращенной конъюнктивной нормальной формы функции ϕ0(x1, x2, …, xn). По импликантной матрице рассмотренным выше способом можно получить минимальные КНФ функции f(x1, x2, …, xn).
Пример. Найти минимальную КНФ функции, записанной таблицей.
x1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
x2 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
x3 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
x4 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
f(x1, x2, x3, x4) |
|
|
|
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
СКНФ эквивалентной функции ϕ1(x1, x2, x3, x4):
48

ϕ1 (x1 , x2 , x3 , x4 ) = (x1 x2 x3 x4 )(x1 x2 x3 x4 )(x1 x2 x3 x4 )
(x1 x2 x3 x4 )(x1 x2 x3 x4 ).
СКНФ функции ϕ0 (x1, x2 , x3 , x4 ) = (x1 x2 x3 x4 )(x1 x2 x3 x4 )
(x1 x2 x3 x4 )(x1 x2 x3 x4 )(x1 x2 x3 x4 )(x1 x2 x3 x4 )(x1 x2 x3 x3 ) (x1 x2 x3 x4 ).
Сокращенная КНФ функции ϕ0(x1, x2, x3, x4)
ϕ0 (x1, x2 , x3 , x4 ) = (x1 x3 )(x2 x4 )(x1 x2 ).
Импликантная матрица имеет вид:
Импли- x x |
|
x |
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
x |
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
2 |
3 |
x |
4 |
1 |
x |
2 |
|
x |
3 |
4 |
x |
1 |
x |
2 |
3 |
4 |
x |
1 |
2 |
x |
3 |
x |
4 |
x |
1 |
x |
2 |
x |
3 |
4 |
|||||||||||||||
канты |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
x1 |
|
|
х |
х |
х |
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
х |
|
|
х |
х |
|
x4 |
|
|
|||||
x1 x2 |
х |
|
|
|
|
||
|
|
|
|
|
|||
Минимальная КНФ функции f(x1, x2, x3, x4)
f (x1 , x2 , x3 , x4 ) = (x1 x3 )(x2 x4 ).
Рассмотренная функция имеет четыре минимальные ДНФ
f (x1, x2 , x3 , x4 ) = x1 x2 x2 x3 x1 x4 . f (x1 , x2 , x3 , x4 ) = x1 x2 x2 x3 x2 x4 . f (x1 , x2 , x3 , x4 ) = x1 x2 x1 x3 x1 x4 . f (x1 , x2 , x3 , x4 ) = x1 x2 x1 x3 x2 x4 .
Здесь больше букв, чем в МКНФ.
49
