
- •Основные понятия и определения
- •1.1. Переключательные функции одного и двух аргументов
- •1.3. Представление переключательной функции в виде многочленов.
- •1.4. Пять классов переключательных функций. Теорема о функциональной полноте
- •Линейные
- •1.5. Функционально полные системы логических функций.
- •1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ГРАФОВ
- •Алгоритм построения минимального каркаса
- •Обоснование алгоритма
- •7. ЭЙЛЕРОВЫ ЦЕПИ И ЦИКЛЫ
- •Алгоритм построения эйлерова цикла
- •Обоснование алгоритма
- •Алгоритм Флойда
На рис. 1а изображен исходный помеченный граф и начальные значения λi. На рис. 1б для того же графа указаны конечные значения λi и выделен кратчайший путь. Пометка вершин графа происходила в следующем порядке (в скобках указана дуга, вдоль которой выполняется (1)):
λ1 = 6 |
(x0, x1), |
λ2 = 7 |
(x0, x2), |
λ3 = 6 |
(x0, x3), |
λ4 = 12 |
(x1, x3), |
λ4 = 11 |
(x2, x4), |
λ5 = 16 |
(x3, x4), |
λ5 = 15 |
(x4, x5), |
λ6 = 18 |
(x4, x6), |
λ6 = 17 |
(x5, x6). |
Иногда возникает задача отыскания кратчайших расстояний между всеми парами вершин. Одним из способов решения этой задачи является
Алгоритм Флойда
Обозначим lij длину дуги (xi, xj), если таковой не существует примем lij = ∞, кроме того, положим lii = 0. Обозначим dij(m) длину кратчайшего из пу-
тей из xi в xj с промежуточными вершинами из множества {x1, …, xm}. Тогда можно получить следующие уравнения
dij(0) = lij , |
(2) |
dij(m+1) = min(dij(m) , dim(m) + dmj(m) ) . |
(3) |
Уравнение (2) очевидно. Обоснуем уравнение (3). Рассмотрим кратчайший путь из xi в xj с промежуточными вершинами из множества {x1, …, xm, xm+1}. Если этот путь не содержит xm+1, то dij(m+1) = dij(m) . Если же он содер-
жит xm+1, то деля путь на отрезки от xi до xm+1 и от xm+1 до xj, получаем ра-
венство dij(m+1) =dim(m) + dmj(m) .
Уравнения (2) и (3) позволяют легко вычислить матрицу расстояний [dij] между всеми парами вершин графа G(X, E). На первом этапе согласно (2)
составляем n×n матрицу [dij(0) ] равную матрице [lij] весов ребер (n – число вершин G(X, E)). n раз производим вычисление по итерационной формуле
(3), после чего имеем [dij(n)
] – матрицу расстояний.
Отметим, что алгоритм Флойда непосредственно не указывает сам кратчайший путь между вершинами, а только его длину. Алгоритм Флойда можно модифицировать таким образом, чтобы можно было находить и сами пути. Для этого получим вспомогательную матрицу [Rij], которая будет содержать наибольший номер вершины некоторого кратчайшего пути из xi в xj (Rij=0, если этот путь не содержит промежуточных вершин).
99
Эта матрица вычисляется параллельно с dij(m+1) по следующим правилам
R(0) |
= 0 |
|
|
|
|
|
ij |
|
|
|
|
|
|
|
|
R(m) , если |
d (m+1) |
= d (m) |
|
|
Rij(m+1) |
|
ij |
ij |
ij |
|
|
= |
|
d (m+1) |
= d (m) + d (m) |
|||
|
|
m +1, если |
||||
|
|
|
|
ij |
im |
mj |
Последнее выражение следует из обоснования (3).
Теперь кратчайший путь выписывается из следующего рекурсивного алгоритма:
Кратчайший путь из xi в xj: |
|
||
1°. Если |
Rij = 0 то выполнить 2°, |
|
|
|
|
иначе выполнить 3°. |
|
2°. Если |
i=j |
то выписать xi и закончить, |
|
|
|
иначе выписать xi и xj закончить. |
|
3°. Выписать кратчайший путь между xi и |
xR . |
||
|
|
|
ij |
4°. Выписать кратчайший путь между xRij и xj.
Пункты 3° и 4° предполагают рекурсивное обращение к рассмотренному алгоритму.
С задачей определения кратчайших путей в графе тесно связана задача транзитивного замыкания бинарного отношения.
Напомним, что бинарным отношением на множестве Х называется произвольное подмножество E X × X.
Транзитивным называется отношение, удовлетворяющее следующему условию: если (x, y) E и (y, z) E, то (x, z) E для всех x, y, z X. Отметим, что бинарное отношение можно однозначно представить орграфом G(X, E). Теперь для произвольного отношения Е определим новое отношение Е* следующим образом
E* = {(x, y) | если в G(X, E) существует путь ненулевой длины из x в y}. Легко проверить, что Е* - транзитивное отношение. Кроме того, Е* является наименьшим транзитивным отношением на Х в том смысле, что для произвольного транзитивного отношения F E выполняется E* F. Отношение Е* называется транзитивным замыканием отношения Е.
Если отношение Е представить в виде графа G(X, E) в котором каждая дуга имеет вес 1, то транзитивное замыкание Е* можно вычислить с помощью алгоритма Флойда. При этом надо учесть, что
(xi, xj) E* если di(,nj) < ∞.
Для большего удобства алгоритм Флойда в этом случае можно модифицировать следующим образом.
Положим
100
0,если(x |
i |
, x |
j |
) E |
|
||
|
|
|
|
|
. |
||
lij = |
|
, x |
|
) E |
|||
1,если(x |
j |
|
|||||
|
i |
|
|
|
|
|
|
Вместо (3) запишем
dij(m+1) = dij(m) (dim(m) dmj(m) ) ,
где – дизъюнкция (логическое сложение),– конъюнкция (логическое умножение).
После завершения работы алгоритма будем иметь
1,если(x |
, x |
j |
) E * |
|
|
i |
|
|
|
dij(n) = |
|
, x |
|
) E * |
0,если(x |
j |
|||
|
i |
|
|
|
Модифицированный таким образом алгоритм называется алгоритмом Уоршелла.
101
x2
x1
x2
x1
x2
x1
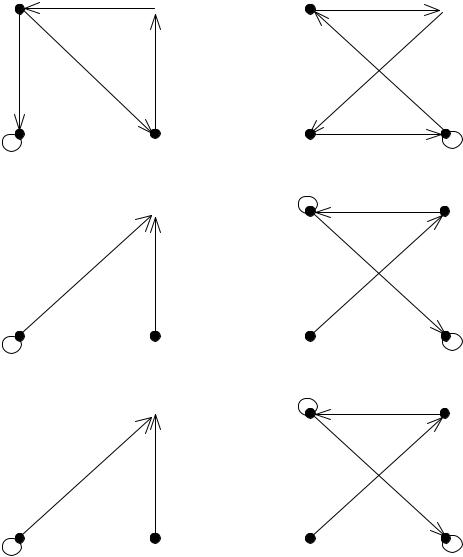
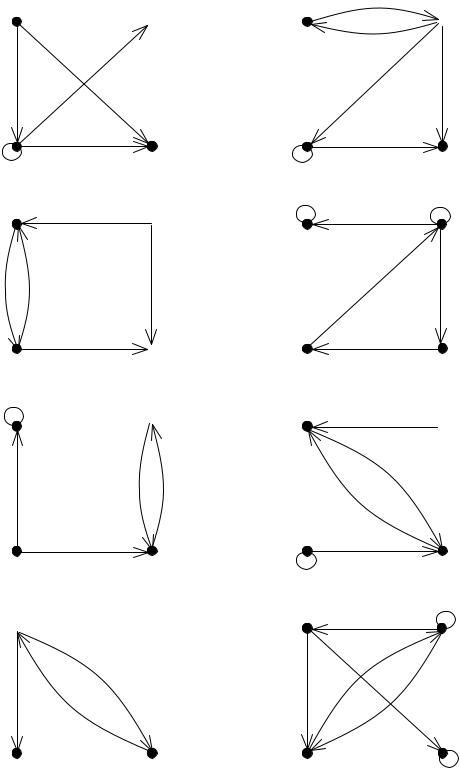
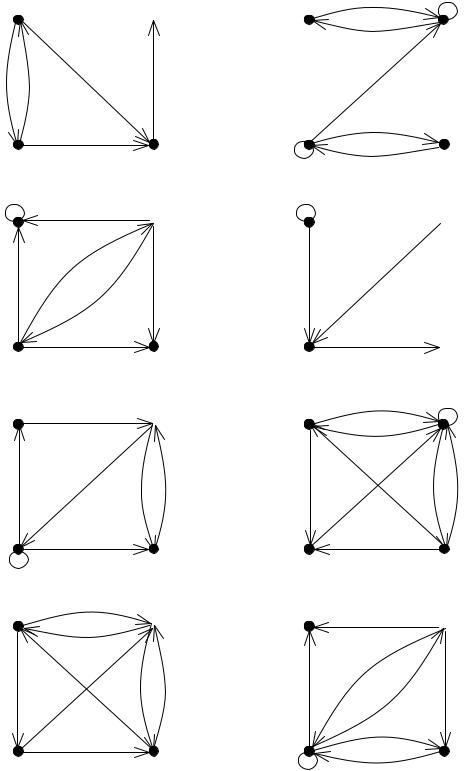
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ
 x3 y2
x3 y2
G1 G2
x4 y1

 x3 y2
x3 y2
G1 G2
x4 y1

 x3 y2
x3 y2
G1 G2
x4 y1
 y3
y3
2
y4
y3
3
y4
y3
4
y4
102
x2
x1
x2
x1
x2
x1
x2
x1
 x3
x3
G1
x4
 x3
x3
G1
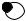 x4
x4
 x3
x3
G1
x4

 x3
x3
G1
x4
y2
G2
y1
y2
G2
y1
y2
G2
y1
y2
G2
y1
 y3
y3
5
y4
y3
6
y4
 y3
y3
7
y4
y3
8
y4
103
x2
x1
x2
x1
x2
x1
x2
x1
 x3
x3
G1
x4
 x3
x3
G1
x4
 x3
x3
G1
x4
 x3
x3
G1
x4
y2
G2
y1
y2
G2
y1
y2
G2
y1
y2
G2
y1
y3
9
y4
 y3
y3
10
 y4
y4
y3
11
y4
 y3
y3
12
y4
104
x2
x1
x2
x1
x2
x1
x2
x1
x3
G1
 x4
x4
 x3
x3
G1
x4
 x3
x3
G1
 x4
x4
 x3
x3
G1
x4
y2
G2
y1
y2
G2
y1
y2
G2
y1
y2
G2
y1
y3
13
y4
y3
14
y4
 y3
y3
15
y4
y3
16
y4
105
x2
x1
x2
x1
x2
x1
x2
x1
 x3
x3
G1
x4

 x3
x3
G1
x4
 x3
x3
G1
x4
 x3
x3
G1
x4
y2
G2
y1
y2
G2
y1
y2
G2
y1
y2
G2
y1
y3
17
y4
y3
18
y4
y3
19
y4
 y3
y3
20
 y4
y4
106
x2
x1
x2
x1
x2
x1
x2
x1
 x3
x3
G1
 x4
x4
 x3
x3
G1
x4

 x3
x3
G1
x4
 x3
x3
G1
x4
y2
G2
y1
y2
G2
y1
y2
G2
y1
y2
G2
y1
y3
21
y4
 y3
y3
22
y4
y3
23
y4
y3
24
y4
107
x2
x1
x2
x1
x2
x1
x2
x1
 x3
x3
G1
x4
 x3
x3
G1
 x4
x4
 x3
x3
G1
x4

 x3
x3
G1
x4
y2
G2
y1
y2
G2
y1
y2
G2
y1
y2
G2
y1
 y3
y3
25
 y4
y4
y3
26
y4
 y3
y3
27
y4
y3
28
y4
108
x2 |
x3 |
y2 |
y3 |
|
G1 |
G2 |
29 |
x1 |
x4 |
y1 |
y4 |
x2 |
x3 |
y2 |
y3 |
|
G1 |
G2 |
30 |
x1 |
x4 |
y1 |
y4 |
109
