
- •Дифференциальное исчисление функций одной переменной
- •2. Правила дифференцирования
- •3. Касательная и нормаль к плоской кривой.
- •5. Производная неявно заданной функции
- •Свойства дифференциала.
- •10. Остаточный член формулы Тейлора
- •11. Вывод формулы Тейлора
- •13. Экстремум необходимое и достаточное условие существования экстремума функции.
Дифференциальное исчисление функций одной переменной
1.
2. Правила дифференцирования
При
дифференцировании константу можно
выносить за производную:
![]() Правило
дифференцирования суммы функций:
Правило
дифференцирования суммы функций:
![]() Правило
дифференцирования разности функций:
Правило
дифференцирования разности функций:
![]() Правило
дифференцирования произведения функций
(правило Лейбница):
Правило
дифференцирования произведения функций
(правило Лейбница):
![]() Правило
дифференцирования частного функций:
Правило
дифференцирования частного функций:
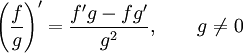 Правило
дифференцирования функции в степени
другой функции:
Правило
дифференцирования функции в степени
другой функции:
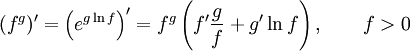 Правило
дифференцирования сложной функции:
Правило
дифференцирования сложной функции:
![]() Правило
логарифма при дифференцировании функции:
Правило
логарифма при дифференцировании функции:
![]()
3. Касательная и нормаль к плоской кривой.
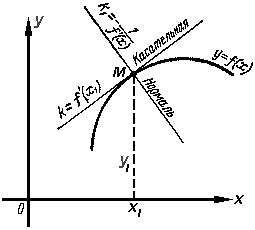 Пусть
даны кривая y = f(x)
и точка M (x1 ; y1)
на ней. Требуется составить уравнения
касательной и нормали (смотри
рисунок).
Как известно,
угловой коэффициент k
касательной к кривой y = f(x)
в точке M (x1 ; y1)
равен значению f '(x1)
производной y' = f '(x)
при x = x1/
Следовательно, уравнение касательной
можно записать в виде уравнения прямой,
проходящей через данную точку в данном
направлении, т.е. в виде
Пусть
даны кривая y = f(x)
и точка M (x1 ; y1)
на ней. Требуется составить уравнения
касательной и нормали (смотри
рисунок).
Как известно,
угловой коэффициент k
касательной к кривой y = f(x)
в точке M (x1 ; y1)
равен значению f '(x1)
производной y' = f '(x)
при x = x1/
Следовательно, уравнение касательной
можно записать в виде уравнения прямой,
проходящей через данную точку в данном
направлении, т.е. в виде
y - y1 = f '(x1)(x - x1)
Нормалью
называется прямая, проходящая через
точку касания перпендикулярно касательной.
поэтому ее угловой коэффициент равен
![]() ,
а уравнение записывается в виде
,
а уравнение записывается в виде
![]()
Производные:
Графики
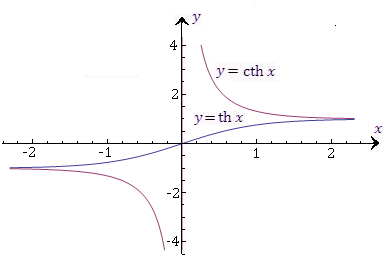 Рис.
5. Графики гиперболических функций
Рис.
5. Графики гиперболических функций
![]() и
и ![]() .
.
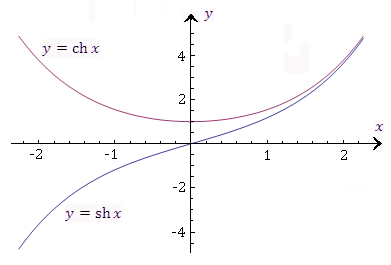 Рис.
3. Графики гиперболических функций
Рис.
3. Графики гиперболических функций
![]() и
и ![]() .
График гиперболического косинуса
называется цепной линией, которая
является линией провисания тяжёлой
нити, подвешенной в двух точках.
.
График гиперболического косинуса
называется цепной линией, которая
является линией провисания тяжёлой
нити, подвешенной в двух точках.
Гиперболический
синус ![]() и гиперболический косинус
и гиперболический косинус ![]() определяются аналитическими выражениями
определяются аналитическими выражениями
![]()
![]()
Эти функции определены и непрерывны на всей числовой оси и тождественно удовлетворяют следующим соотношениям, которые легко проверяются непосредственным вычислением:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Гиперболический
тангенс ![]() и гиперболический котангенс
и гиперболический котангенс ![]() определяются формулами
определяются формулами
![]()
![]()
и представляют собой нечетные функции:
![]()
![]()
4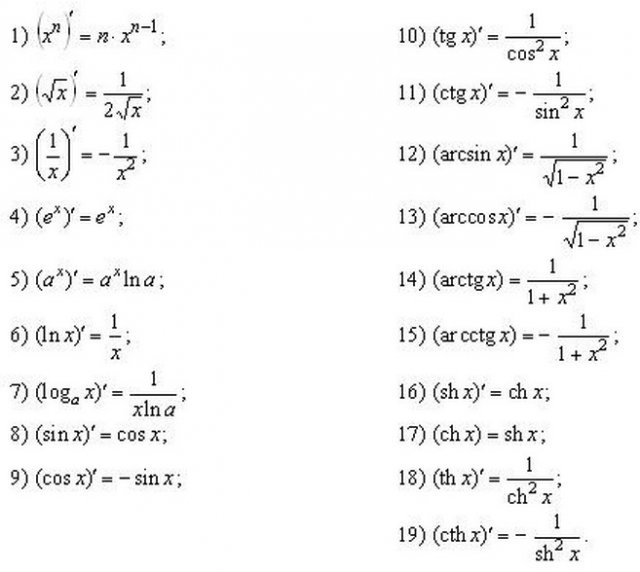 .
.
5. Производная неявно заданной функции
Если y = f(x) - дифференцируемая функция, заданная уравнением F(x, y) = 0, т. е. F(x, f(x)) ≡ 0 на некотором интервале ]a, b[, то во многих случаях ее производную можно найти из уравнения
![]()
![]()
Производная обратной функции
Дифференцируемая монотонная функция f: ]a, b[ → R с необращающейся в нуль производной имеет обратную дифференцируемую функцию f -1, производная которой вычисляется по формуле
![]()
![]()
6. Определение. Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции.
Обозначается dy или df(x).
Из определения следует, что dy = f(x)x или
dy = f(x)dx.
Можно
также записать:
![]()
Инвариантность формы дифференциала
Рассмотрим сложную функцию y=f(u(x)).
Пусть функции y=f(u), u=u(x)
дифференцируемы, тогда
![]()
Таким образом, если аргументом функции является функция другого аргумента, то форма дифференциала совпадает с формой дифференциала (7), когда аргументом функции является независимая переменная. Это свойство называется инвариантностью формы дифференциала.
