
- •1. Определение гидравлики. Основные понятия и определения. Сплошная среда.
- •2. Основные физические свойства жидкостей.
- •3. Силы, действующие в жидкости. Гидростатическое давление - определение.
- •4. Давление абсолютное, избыточное и вакуумметрическое.
- •5. Свойства гидростатического давления.
- •6. Эпюры гидростатического давления.
- •7. Дифференциальные уравнения равновесия жидкости (уравнения Эйлера).
- •8. Основное дифференциальное уравнение гидростатики.
- •9. Основное уравнение гидростатики (закон Паскаля).
- •10 Геометрическое и энергетическое понятия основного уравнения гидростатики.
- •11. Поверхности равного давления
- •12. Относительный покой жидкости
- •3.1.2 Относительный покой при вращении вокруг вертикальной оси
- •13. Сила давления жидкости на плоскую стенку
- •14.Приборы дл измерения давления
- •15. Гидростатический парадокс
- •16. Сила давления на криволинейную поверхность. Тело давления
- •17. Закон Архимеда
- •18. Равновесие тела в покоящейся жидкости
- •19.Определение толщины стенок цилиндрических труб
- •20.Идеальная и реальная жидкости. Закон Ньютона о внутреннем трении
- •22. Гидравлические элементы потока
- •23. Методы определения движения жидкости (метод Лагранжа и метод Эйлера).
- •24 Уравнение неразрывности (уравнение сохранения массы)
- •25. Расход жидкости (массовый, объемный, весовой).
- •26. Уравнение Бернулли для струйки идеальной жидкости. Геометрический и физический смысл уравнения Бернулли.
- •27. Гидравлический и пьезометрический уклоны.
- •28 Графическое представление уравнения Бернулли для струйки идеальной и реальной жидкости.
- •30. Графическое представление уравнения Бернулли для потока идеальной и реальной жидкости.
- •31. Примеры использования уравнения Бернулли (трубка Пито, Пито-Прандтля, расходомеры и т.Д.)
- •3) Расходомер Вентури.
- •4) Формула Торричелли
- •6) Водоструйный насос
- •7)Ракета
- •32. Классификация гидравлических потерь
- •33.Структура потока в области местных сопротивлений
- •34. Эквивалентная длина
- •35. Режимы движения жидкости. Основные понятия. Критерий Рейнольдса
- •36. Основное уравнение равномерного движения
- •37. Эпюры скоростей при ламинарном и турбулентном режимах движения жидкости
- •38. Определение эквивалентной шероховатости. Гидравлически гладкие и шероховатые поверхности
- •39.Метод наложения потерь. Коэффициент сопротивления системы
- •Коэффициент сопротивления системы
- •40. Кавитация.
- •41 Определение гидравлического удара. Прямой и непрямой гидравлический удар. Скорость распространения ударной волны.
- •42.Назначение и классификация трубопроводов.
- •43.Гидравлические характеристики трубопровода (график зависимости потерь напора в трубопроводе от пропускаемого расхода).
- •44.Определение экономически выгодного диаметра трубопровода (график).
3.1.2 Относительный покой при вращении вокруг вертикальной оси
В этом случае на жидкость действуют силы давления, силы тяжести и силы инерции переносного вращательного движения ускорения массовых сил будут равны:
![]()
Дифференциальное уравнение примет вид:
![]() После интегрирования,
с учетом, что
После интегрирования,
с учетом, что
![]() получим
получим
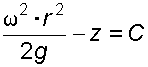

Уравнение (3.11)
является уравнением параболоида
вращения, а поверхности равного давления
образуют семейство параболоидов
вращения, сдвинутых вдоль вертикальной
оси. Каждый параболоид характеризуется
некоторым значением постоянной С. Для
параболоида свободной поверхности
принимаем, что при z=zo
(рис. 3.2) x = y=
0, поэтому c
= -zo.
Тогда уравнение свободной поверхности
примет вид: или
или
![]()
Закон распределения давления по объему жидкости получим из уравнения (2.6), подставив в него соответствующие значения X, Y и Z. После интегрирования получаем:
![]() .
.
Постоянную
интегрирования
![]() определим
из условия, что при
определим
из условия, что при
![]() и
и
![]() ,
т.е.
,
т.е.
![]() .
После подстановки окончательно имеем:
.
После подстановки окончательно имеем:![]() .
.
Для частиц жидкости расположенных на одной вертикали можем записать:
![]() где
где
![]() ,
т.е. существует обычный гидростатический
закон распределения давления.
,
т.е. существует обычный гидростатический
закон распределения давления.
13. Сила давления жидкости на плоскую стенку
Давление жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом, определяется по основному уравнению гидростатики Р=Р0+hρg
Определим силу F давления, действующую со стороны жидкости, на участок рассматриваемой стенки, ограниченный произвольным контуром и имеющий площадь, равную S.
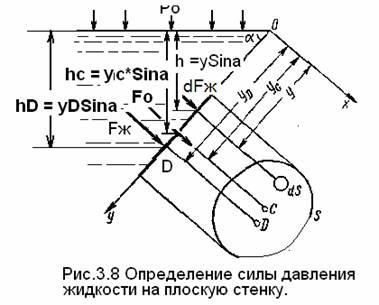
Ось Ох направим перпендикулярно плоскости стенки от точки ее пересечения со свободной поверхностью жидкости, а ось Оу — перпендикулярно оси Ох в плоскости стенки.
Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке dS (давление действующее в точке, одинаково для произвольно расположенной площадки) dFж = P*dS =(P0 + ρhg)dS = P0*dS + ρhg*dS,
где Р0 — давление на свободной поверхности, h — глубина расположения площадки dS. Для определения полной силы Fж проинтегрируем полученное выражение по всей площади S:
![]() ,
,
где у — координата площадки dS, h = у*Sinα .
Последний
интеграл
![]() представляет собой статический
момент площади S
относительно оси Ох
и равен произведению этой площади на
координату ее центра тяжести (точка С),
т. е.
представляет собой статический
момент площади S
относительно оси Ох
и равен произведению этой площади на
координату ее центра тяжести (точка С),
т. е.
![]() Следовательно,
Fж
= P0S+ρg(yc
Sinα)
S
= P0S+ρghcS
(3.11)
Следовательно,
Fж
= P0S+ρg(yc
Sinα)
S
= P0S+ρghcS
(3.11)
здесь hc = (Sinα)yc — глубина расположения центра тяжести площади S, или
Fж = ρg (H0 +hc)S = PcS, (3.12)
Полная сила давления жидкости Fж на плоскую стенку равна произведению площади стенки S на гидростатическое давление Рс в центре тяжести этой площади.
1.В частном случае, когда давление Р0 является атмосферным и действует также с другой стороны стенки, сила Fизб ж избыточного давления жидкости на плоскую стенку равна лишь силеFж давления от веса жидкости, т. е. Fизб ж =Fж = PcS= ρghcS.
2. В общем случае давление Р0 может существенно отличаться от атмосферного, поэтому полную силу F давления жидкости на стенку 6удем рассматривать как сумму двух сил: F0 от внешнего давления Р0 и силы Fж от веса жидкости, т. е. F= F0 + Fж = (P0+Pс)S. (3.13.)
Рассмотрим вопрос о точках приложения этих сил, называемых центрами давления*. Так как внешнее давление Р0 передается всем точкам площади S одинаково, то его равнодействующая F0 будет приложена в центре ус тяжести площади S.
Для нахождения точки приложения силы давления Fж от веса жидкости (точка D) применим теорему механики согласно которой момент равнодействующей силы относительно оси Ох равен сумме моментов составляющих сил, т. е.
![]() где уD
— координата точки приложения силы.
где уD
— координата точки приложения силы.
Ранее уже было найдено выражение для силы от веса жидкости действующей на плоскую стенку, это выражение (3.11): Fж = ρghD*S = ρg(yсSinα)*S и dFж= ρgh*dS= ρg(ySinα)*dS. Используя yс и у, получаем
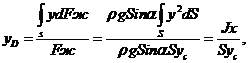 (3.14)где
(3.14)где
![]() - момент инерции площади S
относительно оси Оx.
- момент инерции площади S
относительно оси Оx.
Учитывая,
что Jx
= Jx0+yc2S,
(3.15) Jx0
-
момент инерции площади S
относительно центральной оси, параллельной
оси Ох), находим уD
= ус+
Jx0/(усS),
(3.16.)
Таким образом, точка приложения силы Fж расположена ниже центра тяжести площади стенки; расстояние между ними Δу = Jx0/( усS), (3.17) .
Если давление Р0 равно атмосферному, то точка D и будет центром давления.
При Р0 выше атмосферного центр давления находят по правилам механики, как точку прило-жения равнодействующей двух сил F0 и Fж , чем больше первая сила по сравнению со второй тем, очевидно, центр давления ближе к центру тяжести площади S.
В частном случае, когда стенка имеет форму прямоугольника размерами а × b (рис. 3.9) и одна из его сторон а лежит на свободной поверхности с атмосферным давлением, центр давления D находится па расстоянии b/3 от нижней стороны.
Ранее указывалось, что в жидкостях возможны лишь распределенные силы. Поэтому центры давления можно рассматривать лишь условно.
