2. Группа дифференцирующих звеньев.

Название звеньев этой группы объясняется тем, что они обладают свойством дифференцировать входной сигнал. Признаком дифференцирующих свойств является наличие полинома от p в числителе передаточной функции. Причем, как было показано в [1], у типовых динамических звеньев этот полином не превышает второго порядка. Рассмотрим характеристики наиболее распространенных в автоматических системах звеньев этой группы.

2.1. Идеальное дифференцирующее звено

Идеальным дифференцирующим называется звено, у которого выходная величина прямо пропорциональна производной по времени от входной величины, т.е. звено, динамика которого описывается уравнением

(38)

где k - коэффициент пропорциональности.

После преобразования по Лапласу при нулевых начальных условиях уравнение (38) примет вид:

(39)

Тогда передаточная функция будет:

(40)

Найдем переходную функцию звена, для чего в уравнение (39) подставим изображение входного сигнала :

(41)

По таблицам преобразований Лапласа находим, что оригинал, соответствующий изображению (41), имеет вид:

(42)

Следовательно, переходная функция звена представляет собой мгновенный импульс с площадью равной k.

График переходной функции звена представлен на рисунке 2.1.

Рисунок 2.1. Переходная функция идеального дифференцирующего звена.

Рисунок 2.2. Амплитудно-частотная характеристика идеального дифференцирующего звена.

Для получения частотных характеристик звена делаем подстановку

в передаточную функцию (40), т.е.

(43)

Анализ выражения (43) показывает, что вещественная и мнимая части АФХ равны соответственно:

(44)

Амплитудно-частотная характеристика звена будет определяться выражением

(45)

и представлена на рисунке 2.2, а фазочастотная характеристика:

(46)

представлена на рисунке 2.3.

Из графиков и мы видим, что идеальное дифференцирующее звено пропускает гармонический входной сигнал, усиливая его по амплитуде тем больше, чем больше частота входного сигнала, и обеспечивает постоянный при всех частотах положительный фазовый сдвиг на величину (что означаетопережение по фазе выходного сигнала по отношению к входному на ). Если проанализировать вид амплитудно-фазовой характеристики звена по выражениям (44) для и , либо по и (выражения (45) и (46) соответственно), то можно прийти к выводу, что годограф, описываемый на комплексной плоскости концом вектора при изменении частоты в диапазоне представляет собой прямую, совпадающую с положительной полуосью ординат. График АФХ и распределение частот показаны на рисунке 2.4.

Рисунок 2.3. Фазочастотная характеристика идеального дифференцирующего звена.

Рисунок 2.4. Амплитудно-фазовая характеристика идеального дифференцирующего звена.

2.2. Реальное дифференцирующее звено (дифференцирующее инерционное)

Звено любой физической природы, описываемое дифференциальным уравнением вида

(47)

называется реальным дифференцирующим звеном или дифференцирующим инерционным.

Его передаточная функция, полученная из уравнения (47) после его преобразования по Лапласу при нулевых начальных условиях

(48)

имеет вид:

(49)

Из выражения передаточной функции, представленной в виде следующего произведения

(50)

где , становится понятным название звена. Звено можно рассматривать как последовательное соединение идеального дифференцирующего звена с передаточной функцией и апериодического (инерционного) звена первого порядка с передаточной функцией

а потому оно проявляет свойства и того и другого звена, что и отражается в названии.

Выведем уравнение переходной функции звена. Из уравнения (48) изображение входного сигнала имеет вид:

Подставим в него изображение единичного ступенчатого входного воздействия x_вх(p) = 1/p, получим

(51)

Для удобства нахождения оригинала выражение (51) представим в виде:

Тогда по таблицам преобразования Лапласа оригинал переходной функции будет иметь вид:

(52)

График переходной функции, построенный по уравнению (52), представлен на рисунке 2.5.

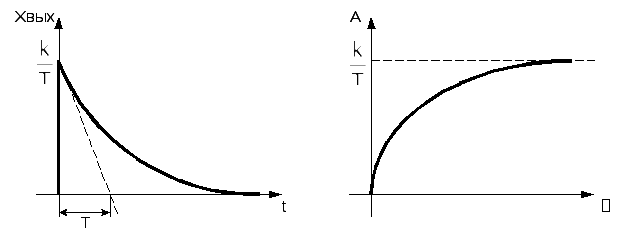
Рисунок 2.5. Переходная функция реального дифференцирующего звена.

Рисунок 2.6. Амплитудно-частотная характеристика реального дифференцирующего звена.

Из графика мы видим, что при ступенчатом входном воздействии выходная величина звена изменяется во времени по импульсному закону. Передний фронт импульса - мгновенный скачок из 0 (начала координат) (напомним, что установившийся режим, существующий до возникновения возмущения, в ТАУ принимается за 0 - начало отсчета изменений выходной величины в динамике) до значения . Задний фронт импульса – инерционный, по закону экспоненты .

Учитывая, что данное звено представляет собой последовательное соединение идеального дифференцирующего звена и апериодического звена 1-о порядка, для нахождения АЧХ и ФЧХ данного звена удобнее всего воспользоваться правилом последовательного соединения звеньев, а именно: перемножить амплитудно-частотные характеристики и сложить фазочастотные. Формулы АЧХ и ФЧХ идеального дифференцирующего звена были выведены в разделе 2.1., а для апериодического звена - в работе [1].

Поэтому АЧХ и ФЧХ реального дифференцирующего звена будут соответственно:

(53)

(54)

Анализ амплитудно-частотной функции (53) показывает, что при , а при - .

График этой функции показан на рисунке 2.6. Из графика видно, что звено можно назвать резонатором высоких частот, т.к. чем выше частота входного сигнала, тем больше значение АЧХ.

График фазочастотной функции (54) представлен на рисунке 2.7. Он показывает, что при всех частотах звено даёт опережение по фазе выходного сигнала по отношению к входному, что свойственно всем звеньям дифференцирующей группы. Максимальный фазовый сдвиг при низких частотах близок к , но с ростом частоты входного сигнала опережение по фазе уменьшается, а при близко к нулю.

Рисунок 2.7. Фазочастотная характеристика реального дифференцирующего звена

Рисунок 2.8. Амплитудно-фазовая характеристика реального дифференцирующего звена

Проанализируем амплитудно-фазовую характеристику звена. Из выражения (49) традиционным способом нетрудно вывести формулы для вещественной и мнимой частотных характеристик

Таким образом:

(55)

(56)

Найдём в явной форме зависимость , воспользовавшись методом, который был применен для апериодического звена первого порядка в работе [1]. Для этого определим сумму квадратов .

Таким образом, получили следующее:

(57)

Преобразуем выражение (57)

(58)

Дополним подчеркнутое выражение в левой части до полного квадрата

Тогда получим:

(59)

Но теперь можно сделать вывод, что выражение (59) на комплексной плоскости в координатах представляет собой уравнение окружности с центром в точке и радиусом . Причём при положительных коэффициентах звена нас будет удовлетворять в качестве графика АФХ только верхняя полуокружность, т.к. из выражений (55) и (56) видим, что при всех и . График АФХ реального дифференцирующего звена представлен на рисунке 2.8.

Аналогичный результат можно получить, если строить график АФХ либо параметрическим способом, т.е. задаваясь значениями , вычисляя и по формулам (55) и (56), а затем пользуясь декартовой системой координат, либо по рассчитанным ранее значениям и в полярной системе координат.