Методические рекомендации к изучению тем курса и выполнению контрольных работ

Раздел 1. Функции нескольких переменных

Тема 1. Основные понятия. Непрерывность

Понятие функции нескольких переменных. Область существования функции. Линии и поверхности уровня функции. Предел функции нескольких переменных. Непрерывность и точки разрыва.

[1], §43.

В контрольной работе рассматриваются только функции двух и трех переменных. Для усвоения теоретического материала и при решении задач можно использовать метод аналогии с функциями одной переменной, хотя с увеличением числа переменных появляются существенные отличия.

Тема 2. Частные производные. Полный дифференциал функции

Определение частных производных. Полное приращение функции. Полный дифференциал функции. Применение полного дифференциала функции к приближенным вычислениям.

[1], §44, п. 44.1, 44.3, 44.4.

В определении частной производной функции используется понятие частного приращения, а в остальном оно совпадает с определением производной функции одной переменной. Правила вычисления частных производных аналогичны правилам, указанным для функций одного переменного, и только требуется каждый раз помнить, по какому переменному ищется производная.

Тема 3. Дифференцирование сложных функций. Дифференцирование неявных функций

[1], §44, п. 44.6-44.8.

Здесь важно усвоить порядок и формулы вычисления производных, если:

1. z = f(x,y) – дифференцируемая функция аргументов х и у, которые, в свою очередь, являются дифференцируемыми функциями независимой переменной t;

2. z = f(x,y), где х = (u,v), y = (u,v), причем u и v – независимые переменные, а f, ,  - дифференцируемые функции;

3. уравнение f(x,y) = 0, f(x,y) – дифференцируемая функция переменных х и у, определяет у как функцию х;

4. уравнение F(x,y,z) = 0, F(x,y,z) – дифференцируемая функция переменных х,у, и z, определяет z как функцию независимых переменных х и у.

Тема 4. Производная в данном направлении. Градиент функции

[3], гл. VIII, §14, 15.

При выполнении задания 2 контрольной работы следует учесть, что в исходных данных приводится вектор , а при вычислении производной по направлению используются косинусы углов между направлениеми соответствующими координатными осями.

Тема 5. Производные и дифференциалы высших порядков

[1], §44, п. 44.2, 44.5.

Определяя производные высших порядков необходимо помнить, что если частные производные, подлежащие вычислению, непрерывны, то результат многократного дифференцирования не зависит от порядка дифференцирования.

Тема 6. Касательная плоскость и нормаль к поверхности

[1], §45.

Поверхность может быть задана уравнением вида z = f(x,y) или F(x,y,z) = 0. Студент должен знать уравнения касательной плоскости и нормали к поверхности в обоих случаях.

Тема 7. Экстремум функции нескольких переменных

Определение экстремума функции. Необходимые условия экстремума. Достаточные условия экстремума. Случай функции многих переменных.

[1], §46.

В задании 4 контрольной работы определяются частные производные 1-го порядка и критические точки, в которых они равны нулю или не существуют и которые лежат внутри области существования функции. Далее каждая критическая точка исследуется с помощью достаточных условий на наличие или отсутствие экстремума.

Раздел 2. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ

Тема 1. Двойной интеграл

Основные понятия и определения. Геометрический и физический смыслы двойного интеграла. Основные свойства двойного интеграла. Вычисление двойного интеграла в декартовых координатах. Вычисление двойного интеграла в полярных координатах. Приложения двойного интеграла.

[2], гл.II, §7.

Решение заданий 5 и 6 контрольной работы №1 следует начинать с построения области интегрирования. В задании 5 в зависимости от порядка интегрирования (в начале по у, затем по х или наоборот) вычисление двойного интеграласводится к вычислению одного или двух двукратных интегралов вида

или

каждый из которых есть результат последовательного вычисления двух обыкновенных определенных интегралов. При этом значение двойного интеграла не зависит от порядка интегрирования.

Рассмотрим пример. Вычислить двойной интеграл 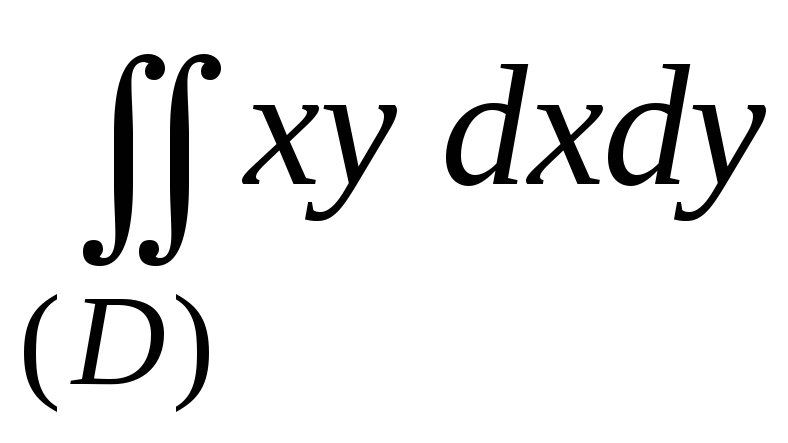, если областьD – треугольник, ограниченный прямыми х=0, 2у-х=0, х+у=3.

Если в начале интегрировать по у, а затем по х, то двойной интеграл по области D выражается одним двукратным интегралом

Вычисляя двукратный интеграл, получим:

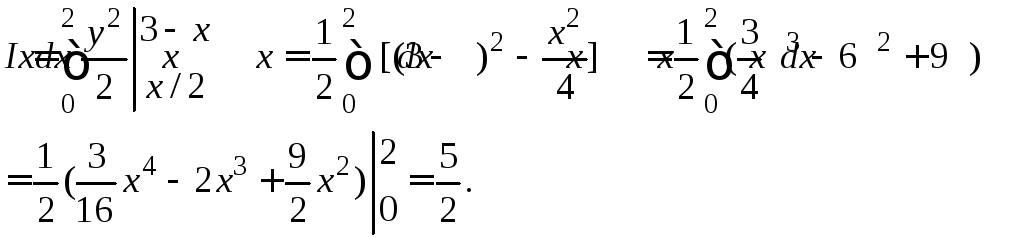
Если интегрировать в другом порядке – сначала по х, а затем по у, необходимо разбить область интегрирования прямой у=1 на две части, так как правая линия границы состоит из двух участков, которые имеют различные уравнения: х=2у и х=3-у. Вследствие этого вычисления несколько усложняются:

В задании 6 область интегрирования представляет собой часть (или части) круга или кольца. Для преобразования двойного интеграла, отнесенного к прямоугольным координатам, в двойной интеграл в полярных координатах нужно в подынтегральном выражении прямоугольные координаты заменить полярными: х = r∙cos, y = r∙sin, а вместо dxdy подставить rdrd. При этом уравнения линий, ограничивающих область интегрирования, также преобразуются к полярным координатам. Например, полярное уравнение окружности х² + у² = R² – r = R, 0    ; полярное уравнение отрезка прямой х = а или у = b − r = а/cos или r = b/sin соответственно (₁≤≤₂).