Тема 5. Ряды Фурье

Периодические функции. Периодические процессы. Тригонометрический ряд Фурье. Теорема Дирихле. Разложение функций в ряд Фурье.

[2], гл.VI, §20, §21. П.21.1-21.4.

При разложении данной функции в ряд Фурье, после нахождения общих выражений для коэффициентов а_n и b_n, следует проверять, будут ли они пригодны при всех значениях n. Для тех значений n, при которых эти общие выражения теряют смысл, необходимо вычислять соответствующие коэффициенты отдельно, подставляя эти исключительные значения n в общие формулы Фурье.

Задания контрольной работы № 1

В задачах 1-10 найти и изобразить область существования функции:

1. 

2. 

3. 

4. z = ln(– x – y) + 8x – y.

5. 

6. 

7. 

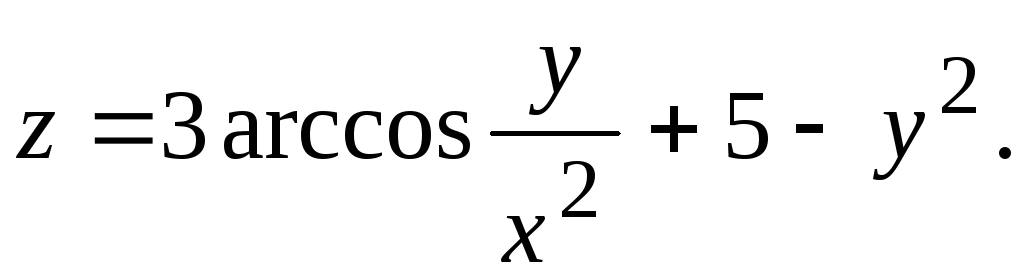
8. z = arcos(x – y) + xy.

9. z = 2 – ln(y – x).

10. z = 5arcsin(yx) + x² – x.

В задачах 11-20 даны функция u = f(x,y,z), точка А и вектор . Требуется найтиgradu в точке А и производную в точке А по направлению вектора .

11. u = x³y²z; A(1;2;3);

12. A(2;1;1);

13. u = xy + z ln(z/y); A(3;-1;-1);

14. A(1;-1;1);

15. u = ln(3x + 2y² + z³); A(-1;2;1);

16. u = 2x – y – z + e^x-2y-z; A(3;1;1);

17. u = xy² – 2z² + 3cos(3x + y – 2z); A(1;1;2);

18. u = 2tg(z³ – 2y² – 3x); A(2;-1;2);

19. ; A(-1;1;-1);

20. u = 3xyz – 2sin(x – 2y + 5z); A(-1;2;1);

В задачах 21-30 найти уравнения касательной плоскости и нормали к поверхности:

21. х² + 2у² + 3z² = 6 в точке (1;-1;1).

22. 4z = х² + у² в точке (2;2;2).

23. x + 2y – lnz + 4 = 0 в точке (2;-3;1).

24. 4х² + 4у² + z² = 4 в точке (12/13;-3/13;8/13).

25. z = x + ln(y/z) в точке (1;1;1).

26. 3^x/z + 3^y/z = 12 в точке (2;1;1).

27. х² – z(2y – 3) = 0 в точке (3;6;1).

28. z = в точке (1;1;7).

29. z = в точке (1;1;5/2).

30. хe^y + уe^z + ze^x = 3e в точке (1;1;1).

В задачах 31-40 исследовать функцию на экстремум.

31.

32.

33.

34.

35. z = 2lnx + 3ln(y/6) + ln(12 – x – y) – 3.

36.

37.

38.

39.

40.

В задачах 41-50 дан двойной интеграл по области (D), ограниченной заданными линиями. Требуется:

а) построить область (D);

б) перейти к одному двукратному и расставить пределы интегрирования по области (D);

в) перейти к двум двукратным и расставить пределы интегрирования по области (D);

г) вычислить массу пластинки, занимающей область (D), при заданной поверхностной плотности f(x,y).

41. 3х – 7у + 2 = 0; 3х – 8у + 1 = 0; у = 2; f(x,y) = x + 3.

42. 3x + 4y – 11 = 0; 3x + 2y – 7 = 0; x =–3; f(x,y) = y – 2.

43. 4х – 3у – 7 = 0; 2х – 3у + 1 = 0; у =–1; f(x,y) = x + 2.

44. х – 5у + 7 = 0; 4х – 5у + 13 = 0; x = 3; f(x,y) = y – 1.

45. 3х + 2у + 5 = 0; 3х + 4у + 1 = 0; у =–4; f(x,y) = x + 3.

46. 2х – 3у + 5 = 0; 8х – 3у – 7 = 0; x =–1; f(x,y) = y + 1.

47. 4х + 3у – 10 = 0; 4х + 7у –2 = 0; у = 2; f(x,y) = x + 3.

48. 6х + 5у – 13 = 0; 3х + 5у – 19 = 0; x = 3; f(x,y) = y + 1.

49. 2х – у – 3 = 0; 4х + 3у – 11 = 0; у = 5; f(x,y) = x+1.

50. х + 5у + 7 = 0; х – у + 1 = 0; x = 3; f(x,y) = y + 2.

В задачах 51-60 перейти к полярным координатам и вычислить интегралы:

51.

52.

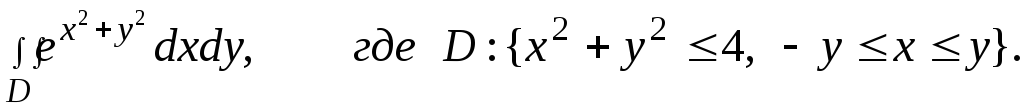
53.

54.

55.

56.

57.

58.

59.

60.

В задачах 61-70 определить массу дуги кривой, если линейная плотность в каждой точке дуги равна (х,у).

61. ; от точки О(0;0) до точки А(2;2);(х,у) = ху.

62. y = lnx; от точки А(1;0) до точки В(2;ln2); (х,у) = х².

63. Полуокружность: х² + у² = 1, у  0; (х,у) = у.

64. ; от точки А(1;1) до точки В(2;1/2);(х,у) = х³/у².

65. у = cosx; от точки А(0;1) до точки В(π/2;0); (х,у) = уsinx.

66. y = e^x; от точки А(0;1) до точки В(1;е); (х,у) = у².

67. ; от точки О(0;0) до точки А(1;);(х,у) = хе^у – х².

68. у =; от точки А(1;1) до точки В(4;2);(х,у) = 2у.

69. ; от точки А(0;1) до точки В(3;2); (х,у) = ху.

70. от точки О(0;0) до точки А(π/2;0);(х,у)= 2у.

В задачах 71-80 найти работу силового поля вдоль дуги плоской кривойL, заключенной между точками А и В.

71.

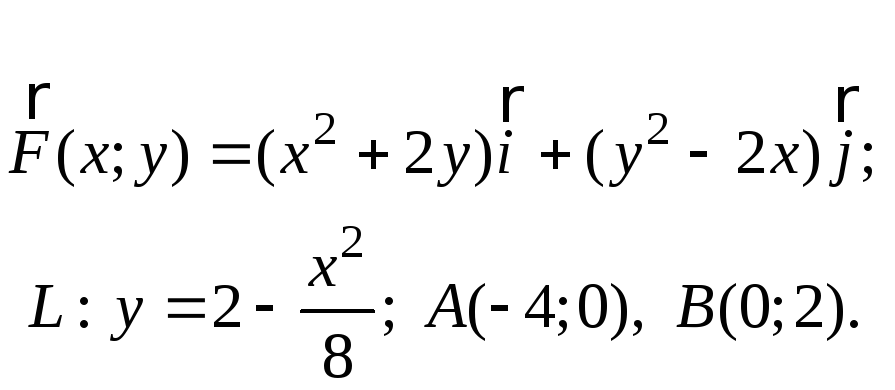
72.

73.

74.

75.

76.

77.

78.

79.

80.