Тема 4. Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами

Интегрирование линейных однородных уравнений высших порядков с постоянными коэффициентами. Структура общего решения линейного неоднородного дифференциального уравнения второго порядка. Метод вариации произвольных постоянных. Интегрирование линейного неоднородного дифференциального уравнения с постоянными коэффициентами и правой частью специального вида.

[2], гл.I, §4,5.

В задании 2б) контрольной работы №2 частное решение у_чн можно найти методом неопределенных коэффициентов. По виду правой части можно заранее указать вид частного решения, где неизвестны лишь числовые коэффициенты, и затем найти его без всяких квадратур в следующих случаях:

1) правая часть – многочлен;

2) правая часть – е^mx[acos(nx)+bsin(nx)];

3) правая часть есть сумма или произведение предыдущих функций.

Общее решение у_он линейного неоднородного уравнения равно сумме какого-либо его частного решения у_чн и общего решения у_оо соответствующего однородного уравнения.

В задании 3 применяется более общий прием решения неоднородного линейного дифференциального уравнения – метод Лагранжа или метод вариации произвольных постоянных.

Если известна фундаментальная система решений у₁, у₂ однородного уравнения y''+py'+qy=0, то общее уравнение соответствующего неоднородного уравнения y''+py'+qy=f(x) может быть найдено по формуле

у=С₁(х)у₁+С₂(х)у₂,

где С₁(х) и С₂(х) – функции, удовлетворяющие системе уравнений

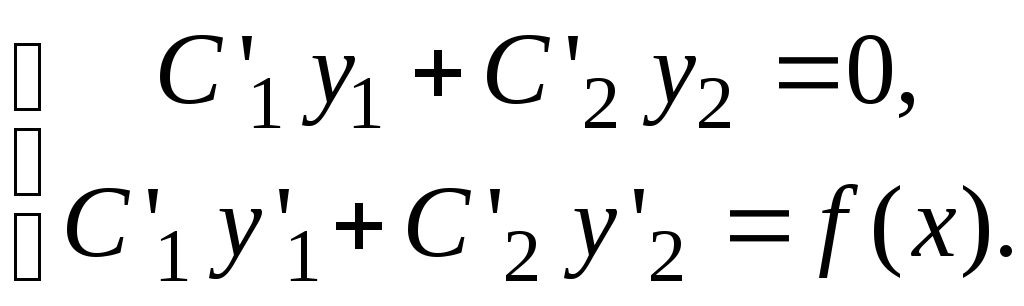
Отсюда

Тема 5. Системы дифференциальных уравнений

Основные понятия. Интегрирование нормальных систем. Системы линейных дифференциальных уравнений с постоянными коэффициентами.

[2], гл.I, §6.

Матричный метод. Нормальная линейная однородная система 2-го порядка с постоянными коэффициентами имеет вид

(*)

или, в матричной форме,

где

Из характеристического уравнения

det(A-λE)=0

находятся различные действительные корни λ₁, λ₂ (в задании 4 контрольной работы №2 рассматривается только этот случай) – собственные значения матрицы А. Для каждого λ определяется соответствующее ему частное решение

где Y^(λ) – собственный вектор матрицы А, соответствующий собственному значению λ (т.е. АY^(λ)= λ Y^(λ), Y^(λ)≠0). Общее решение системы (*) имеет вид

или

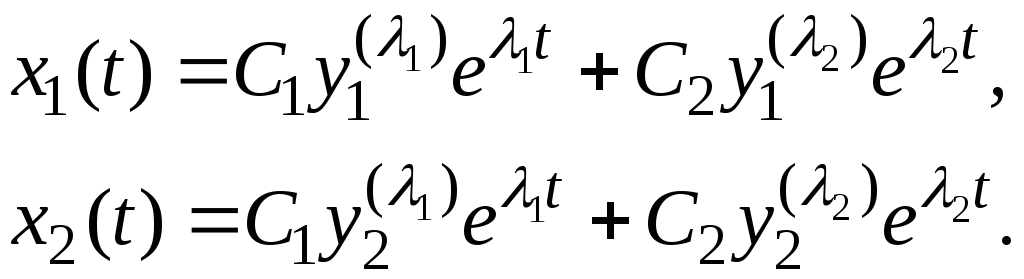
Пример. Найти общее решение системы

Решение. Характеристическое уравнение

имеет действительные и различные корни λ₁=-1, λ₂=5.

Собственные векторы, например, таковы

Поэтому

,

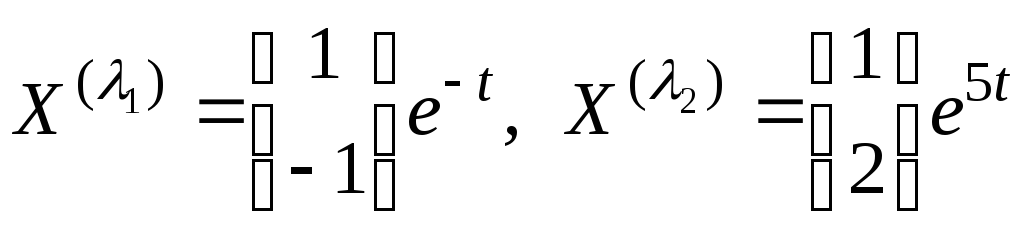отсюда общее решение имеет вид

или

Раздел 4. Ряды

Тема 1. Числовые ряды

Основные понятия. Ряд геометрической прогрессии. Необходимый признак сходимости числового ряда. Гармонический ряд.

[2], гл.IV, §14.

Ряд может сходиться лишь при условии, когда общий член ряда а_n при неограниченном увеличении его номера n стремится к 0: (это необходимый, но недостаточный признак сходимости для всякого ряда.)

Если же , то ряд расходится (это достаточный признак расходимости для всякого ряда.)