Тема 2. Тройной интеграл

Основные понятия. Вычисление тройного интеграла в декартовых координатах. Замена переменных в тройном интеграле. Некоторые приложения тройного интеграла.

[2], гл.II, §8.

Тема 3. Криволинейный интеграл I рода

Основные понятия. Вычисление криволинейного интеграла I рода. Некоторые приложения криволинейного интеграла I рода.

[2], гл.III, §9.

Вычисление массы дуги кривой в задаче 7 контрольной работы сводится к вычислению обыкновенного определенного интеграла: исходя из уравнения линии интегрирования, подынтегральное выражение криволинейного интеграла преобразуется к одной переменной, значения которой в начале и в конце дуги будут пределами полученного обыкновенного интеграла.

Тема 4. Криволинейный интеграл II рода

Основные понятия. Вычисление криволинейного интеграла II рода. Формула Остроградского-Грина. Условия независимости криволинейного интеграла II рода от пути интегрирования. Некоторые приложения криволинейного интеграла II рода.

[2], гл.III, §10.

Указание к решению задачи 7 носит общий характер и в полной мере применимо к решению задачи 8.

Пример. Вычислить криволинейный интеграл

от точки А(1;4) до точки В(2;1) по дуге кривой у=4/х².

Решение. Пользуясь данным уравнением линии интегрирования, преобразуем криволинейный интеграл II рода в обыкновенный определенный интеграл с переменной х, затем вычисляем его:

Раздел 3. Дифференциальные уравнения

Тема 1. Общие сведения о дифференциальных уравнениях

Основные понятия. Задачи, приводящие к дифференциальным уравнениям.

[2], гл.I, §1.

Тема 2. Дифференциальные уравнения первого порядка

Основные понятия. Уравнения с разделяющимися переменными. Однородные дифференциальные уравнения. Линейные уравнения. Уравнение в полных дифференциалах.

[2], гл.I, §2, п. 2.1.-2.5.

Уравнения с разделяющимися переменными могут быть записаны в виде

y’=f(x)g(y),

а также в виде

М(х)N(y)dx+M₁(x)N₁(y)dy=0.

Для решения такого уравнения надо обе его части умножить или разделить на такое выражение, чтобы в одну часть уравнения входило только х, а в другую – только у, и затем проинтегрировать обе части.

Заметим, что при делении обеих частей уравнения на выражение, содержащее переменные х и у, могут быть потеряны решения, обращающие это выражение в нуль.

Уравнения вида y'=f(ax+by) приводятся к уравнениям с разделяющимися переменными заменой z = ax+by (или z=ax+by+c, где с – любое).

Тема 3. Дифференциальные уравнения высших порядков

Основные понятия. Уравнения, допускающие понижение порядка. Линейные дифференциальные уравнения высших порядков. Линейные однородные дифференциальные уравнения второго и n-го порядка.

[2], гл.I, §3.

В задании 2а) контрольной работы №2 рассматриваются дифференциальные уравнения вида F(x, y', y'')=0 и F(y, y', y'')=0. В первом случае порядок уравнения можно понизить, взяв за новую неизвестную функцию низшую из производных, входящих в уравнение, т.е. сделав замену z = y'. Во втором случае порядок уравнения можно понизить, взяв за новое независимое переменное у, а за неизвестную функцию y'=p(y).

Пример. Решить уравнение

yy”=y’²-y’³.

Решение. В уравнение не входит х. Полагаем y'=p(y). Тогда

Подставляя y'=p и y''=p'p в уравнение, получим

yp'p=p²-p³.

Порядок уравнения понижен.

Пусть р≠0. Тогда получаем дифференциальное уравнение с разделяющимися переменными

.

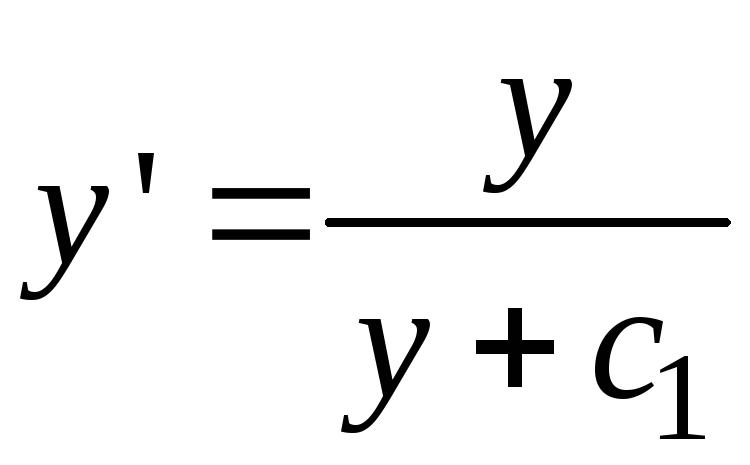Решив полученное уравнение, найдем . Следовательно,. Из этого уравнения получим

у+C₁∙ln|y|=x+C₂.

Если р=0, т.е. y'=0, то получаем решение у=С.

Ответ: у+С₁ln|y|=x+C₂; y=C.