Тема 2. Признаки сходимости и расходимости знакоположительных рядов

Признаки сравнения рядов. Признак Даламбера. Радикальный признак Коши. Интегральный признак Коши. Обобщенный гармонический ряд.

[3], гл.IV, §14.

Отметим «эталонные» ряды, часто используемые для сравнения:

1) геометрический ряд - сходится при |q|<1, расходится при |q|≥1;

2) гармонический ряд - расходится;

3) обобщенный гармонический ряд - сходится при р>1, расходится при р≤1.

Интегральным признаком Коши можно пользоваться, когда выражение общего члена а_n= f(n) имеет смысл не только для целых положительных значений n, но и для всех n, больших некоторого положительного числа N.

Тема 3. Знакочередующиеся и знакопеременные ряды. Признак Лейбница.

Общий достаточный признак сходимости знакопеременных рядов. Абсолютная и условная сходимости числовых рядов.

[2], гл.IV, §15.

При практическом использовании рядов (сходящихся) обычно ограничиваются несколькими их первыми членами. Допускаемая при этом ошибка (остаток ряда) наиболее просто оценивается для знакочередующихся рядов:

ошибка при замене суммы сходящегося знакочередующегося ряда суммой нескольких его первых членов меньше абсолютного значения первого из отброшенных членов.

Тема 4. Степенные ряды

Функциональные ряды. Сходимость степенных рядов. Интервал и радиус сходимости степенного ряда. Разложение функций в степенные ряды. Ряды Тейлора и Маклорена. Некоторые приложения степенных рядов.

[2], гл.V, §§16-19.

Для определения области сходимости функциональных рядов обычно вначале используется признак Даламбера, а затем те значения х, для которых этот признак не решает вопроса о сходимости ряда, исследуются особо, с помощью других признаков сходимости рядов.

Пример. Исследовать на сходимость ряд

Решение. Применим признак Даламбера:

Далее определяем, при каких значениях х этот предел будет меньше единицы, т.е. решаем неравенство <1; |x+1|<2; −3<x<1.

Согласно признаку Даламбера, при любом значении х из найденного интервала данный ряд сходится (абсолютно), а при x<–3 и x>1 расходится.

Граничные точки х=–3 и х=1 этого интервала, для которых признак Даламбера не решает вопроса о сходимости ряда, исследуем особо.

При х=–3 получим числовой знакочередующийся ряд , который сходится согласно признаку Лейбница (члены этого ряда убывают по абсолютной величине, стремясь к нулю.)

При х=1 получим числовой ряд с положительными членами , который расходится (он представляет собой обобщенный гармонический ряд с показателем р=1/2<1). Следовательно, областью сходимости данного степенного ряда является полуоткрытый интервал –3≤х<1.

При решении задания 7 контрольной работы №2 целесообразно использовать разложение в ряд Маклорена элементарных функций sinx, cosx, (1+x)^m, 1/(1-x), ln(1+x), arctgx.

Степенные ряды имеют различные приложения. С их помощью вычисляют с заданной точностью значения функций, определенных интервалов, которые являются «неберущимися» или слишком сложными для вычислений, интегрируются дифференциальные уравнения.

Рассмотрим определенный интеграл

Пусть подынтегральная функция f(x) разлагается в степенной ряд

сходящийся в интервале (-R;R), который содержит отрезок интегрирования [a;b].

Применяя теорему о почленном интегрировании степенных рядов, можно представить интеграл в виде числового ряда

Если ряд сходится достаточно быстро, то можно приближенно вычислить определенный интеграл с помощью частичной суммы ряда

Погрешность результата складывается:

- из погрешности замены ряда частичной суммой; эта погрешность равна остатку ряда;

- погрешностей округления при вычислении частичной суммы.

Для знакочередующегося ряда остаток оценивается в соответствии с замечанием к теме 3 раздела 4. Для оценки остатка ряда в других случаях применяют мажорирование такими числовыми рядами, остатки которых легко оцениваются.

Пример. Вычислить приближенно с точностью до =0,0001

Решение. Пользуясь рядом Маклорена для cosx и заменяя в нем х на х, имеем

Интегрируя в пределах от 0 до 1, получим

Пятый член этого знакочередующегося 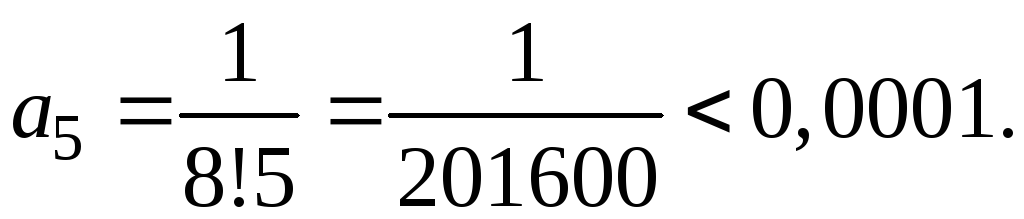ряда Поэтому для вычисления искомого приближенного значения интеграла достаточно взять сумму четырех первых членов ряда: