Угол между двумя прямыми

Пусть прямые l₁ и l₂ заданы своими уравнениями с угловыми коэффициентами: l₁: y=k₁х+b₁, l₂: y=k₂x+b₂, тогда острый угол между двумя прямыми определяется его тангенсом по формуле

.

Если прямые l₁ и l₂ заданы общими уравнениями А₁х+В₁у+С₁=0 и А₂х+В₂у+С₂=0, то угол между ними можно найти как угол между их нормальными векторами

.

В случае задания прямых своими каноническими уравнениями

угол между прямыми находится как угол между направляющими векторами прямых

.

Условия параллельности и перпендикулярности прямых (Табл. 2)

Таблица 2

№ п/п	Способ задания прямых	Условие параллельности прямых	Условие перпендикулярности прямых
1	l1: y=k1х+b, l2: y=k2x+b2	k1=k2	k1k2= -1
2	l1: А1х+В1у+С1=0 l2: А2х+В2у+С2=0		A1A2+B1B2=0
3	l1: l2:		m1m2+n1n2=0

Расстояние от точки до прямой

Пусть прямая l задана уравнением Ах+Ву+С=0, точка М₀(х₀,у₀). Расстояние от точки М₀(х₀,у₀) до прямой l определяется как

.

Примеры решения типовых задач

1. Написать уравнение прямой, отсекающей на оси Оу отрезок b=-3 и составляющей с осью Ох угол 60˚.

Решение:

Воспользуемся уравнением прямой с угловым коэффициентом y=kx+b. По условию b=-3, а k=tgα=tg60˚=3. Итак, у=х-3 – уравнение искомой прямой.

Ответ: у=х-3.

2. Определить параметры k и b для каждой из прямых:

1) 3х+4у=12;

2) 2х+3у=0;

3) у=-2;

4)

Решение:

1) 3х+4у=12; 2) 2х+3у=0; 3) y=-2; 4) ;

4у=12-3х; 3y=-2x; k=0, b=-2. ;

у=;y=; y=4-;

y=; k=,b=0. y=-;

y=; k=,b=4.

k =,b=3.

Ответ: 1) k=,b=3; 2) k=,b=0; 3) k=0, b=-2; 4) k=,b=4.

3. Дан треугольник с вершинами А(-1;1), В(1;5), С(3;-2). Написать уравнения сторон треугольника.

Решение:

Воспользуемся способом задания прямой по 2-м точкам:

АВ: ; BC:; AC:;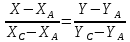

; ;;

. ..

Ответ: АВ: ; ВС:; АС:.

4. Дана прямая 2х+3у-3=0 и точка М₀(1;-2). Написать уравнение прямой, проходящей через точку М₀: а) параллельно заданной прямой; б) перпендикулярно заданной прямой.

Решение:

1-й способ.

а) Условие параллельности двух прямых k₁=k₂.

Пусть уравнение искомой прямой имеет вид y=k₂x+b₂; 3y=3-2x; y=;k₁= k₂=;у=b₂. Так как М₀(1;-2) принадлежит прямой, то -2=1+ b₂ b₂=-2+,b₂=. Итак,y=3у+2х+4=0.

б) Условие перпендикулярности двух прямых k₁k₃=-1.

Пусть уравнение искомой прямой имеет вид y=k₃x+b₃; k₁= k₃  k₃=;y=x+b₃. Так как М₀(1;-2) принадлежит прямой, то -2=1+ b₃ b₃=-2 b₃=.

Итак, 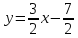3x-2у-7=0.

2-й способ.

.

М₀(1;-2)

Рис.2

а) Из общего уравнения прямой 2х+3у-3=0 определяем координаты вектора нормали . Если искомая прямая параллельна заданной, то векторбудет являться нормалью и к искомой прямой (рис.2). Мы имеем нормаль и точку М₀(1;-2), через которую проходит искомая прямая, поэтому используем уравнение прямой, проходящей через точку М(х₀,у₀) перпендикулярно вектору .

А(х-х₀)+В(у-у₀)=0, 2(х-1)+3(у+2)=0, 2х+3у+4=0.

б) Если искомая прямая l₁ (рис.3) перпендикулярна заданной l, то вектор 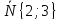, будет параллелен прямойl₁, и мы возьмем его в качестве направляющего вектора искомой прямой .

l

.

2х+3у-3=0

М(1;-2)

l₁

Рис.3

Используем уравнение прямой, проходящей через точку М(х₀,у₀) параллельно вектору .. У нас.; 3х-3=2у+4, 3х-2у-7=0.

Ответ: 2х+3у+4=0, 3х-2у-7=0.

2. Найти расстояние от точки М₀(2;-1) до прямой 3х+4у-22=0.

Решение:

;х₀=2; у₀=-1.

А=3; В=4; С=-22.

.

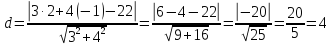Ответ: 4.