Крат. и криволин. интегр

Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения Кафедра «Высшая и прикладная математика»

П.И. Гниломедов

Н.В. Казанцева

КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ

ИНТЕГРАЛЫ

Учебно-методическое пособие для студентов специальностей 190300 – «Подвижной состав», 190303 – «Электрический транспорт железных дорог», 190302 – «Вагоны»

Екатеринбург Издательство УрГУПС 2012

УДК 517 Г90

Гниломедов, П. И.

Г90 Кратные и криволинейные интегралы. : учеб.-метод. пособие / П. И. Гниломедов, Н. В. Казанцева – Екатеринбург : Изд-во УрГУПС, 2012. − 58, [2] с.

Пособие содержит теоретические сведения из разделов «Двойные, тройные и криволинейные интегралы» курса «Высшая математика». Рассмотрен ряд примеров практического характера, иллюстрирующих содержание каждого раздела, приведены задачи для самостоятельной работы студентов. Включены задания типового расчета, связанные с применением изученных методов интегрирования.

Предназначено для проведения практических занятий и организации самостоятельной работы студентов технических специальностей 190300 – «Подвижной состав», 190303 – «Электрический транспорт железных дорог», 190302 – «Вагоны».

УДК 517

Печатается по решению редакционно-издательского совета университета.

Авторы: П. И. Гниломедов, доцент кафедры «Высшая и прикладная математика», канд. пед. наук, УрГУПС;

Н. В. Казанцева, доцент кафедры «Высшая и прикладная математика», канд. физ.-мат. наук, УрГУПС

Рецензенты: П. П. Скачков, доцент кафедры «Высшая и прикладная математика», канд. физ.-мат. наук, УрГУПС;

А. Г. Кесарев, научный сотрудник лаборатории прочности ИФМ УрО РАН, д-р физ.-мат. наук

© Уральский государственный университет путей сообщения (УрГУПС), 2012

Оглавление
ГЛАВА 1. КРАТНЫЕ ИНТЕГРАЛЫ.............................................................	4
1.1. Двойной интеграл и его вычисление двукратным
интегрированием ................................................................................	4
1.2. Тройной интеграл и его вычисление трехкратным
интегрированием ..............................................................................	12
1.3. Механические и физические приложения кратных
интегралов.........................................................................................	17
ГЛАВА 2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ .........................................	26
2.1. Криволинейный интеграл 1-го рода ................................................	26
2.2. Криволинейный интеграл 2-го рода ................................................	30
2.3. Физические и геометрические приложения
криволинейных интегралов..............................................................	35
Библиографический список .........................................................................	41
Варианты заданий типового расчета ............................................................	42

3

ГЛАВА 1. КРАТНЫЕ ИНТЕГРАЛЫ

1.1.Двойной интеграл и его вычисление двукратным интегрированием

Определение

Пусть в некоторой плоской области А задана функция f(x; y). Раздробим область А с помощью сетки на части (ячейки) (рис. 1) А1, А2.....

Аn с площадями F1, F2......Fn и диаметрами d1, d2,....dn. Обозначим через λ наибольший диаметр dk. Выберем в каждой ячейке Ak по точке (xk; yk) и вычислим в этой точке значение нашей функции.

y

…

А3

А2 Аk

А1

…

… А

0

x

Рис. 1

Умножим найденное значение f(x; y) на площадь ячейки Fk. Най-

n

дем сумму таких произведений: σ = ∑ f (xk ; yk )Fk .

k =1

Измельчая дробление, найдем конечный предел: I = limσ.

λ→0

Этот предел называется двойным интегралом от функции f(x; y) по области А и обозначается I = ∫∫ f (x; y)dxdy или I = ∫∫ f (x; y)dF .

A A

Сумма σ называтся интегральной суммой, или суммой Римана.

4

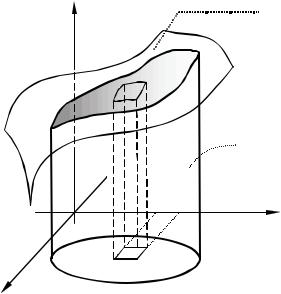
Геометрический смысл двойного интеграла

Если f (x; y) > 0, то ∫∫ f (x; y)dxdy =V , где V – объем тела Т, огра-

A

ниченного снизу плоскостью z = 0, сверху поверхностью z = f(x; y), а с боков цилиндрической поверхностью, образующие которой параллельны оси Oz, а направляющей служит контур фигуры А (рис. 2).

z	z = f ( x ; y )

T

z

0

dy

y

d x dF

x

Рис. 2

Вычисление двойного интеграла

Двойной интеграл вычисляется с помощью вукратного интегрирования.

	b	y2
∫∫ f (x; y)dxdy = ∫dx ∫ f (x; y)dy .
A	a	y1

Выражение, стоящее в правой части формулы, называется повторным (двукратным) интегралом. Для его вычисления необходимо по-

5

г) первая четверть эллипса

следовательно произвести два обыкновенных интегрирования, сна-

y2

чала найти внутренний интеграл ∫ f (x; y)dy , в котором аргумент x

y1

закреплен, а затем проинтегрировать функцию, зависящую уже только от x, между постоянными пределами a и b. При необходимости порядок интегрирования может быть изменен

	d	x2
∫∫ f (x; y)dxdy = ∫dy ∫ f (x; y)dx.
A	c	x1

Значение двойного интеграла не зависит от порядка интегрирования. Для экономии времени расчета следует выбирать такой порядок интегрирования, при котором нет необходимости разбивать область интегрирования на части.

В полярных координатах x = ρ cosφ, y = ρ sinφ:

	β	ρ2 (ϕ)
I = ∫∫ f (ρcos ϕ;ρsin ϕ)ρdρdϕ = ∫dϕ ∫ ρf (ρcos ϕ;ρsin ϕ)dρ.
A	α	ρ1 (ϕ)

Пример. Вычислить двойной интеграл ∫∫xydxdy , если область D:

D

а) прямоугольник, ограниченный прямыми x = 0, x = 3, y = 0, y = 2; б) ограничена прямой y = x – 4 и параболой y2 = 2x;

в) верхняя часть круга x2 + y2 ≤ 4 ;

x2 + y2 ≤1 .

14

Решение (а)

Построим область интегрирования – прямоугольник (рис. 3). Гра-

		0	≤ x ≤3,
ницы области D определяются системой D :		0	≤ y ≤ 2 .
	3	2		3	2
Тогда двойной интеграл равен ∫∫xydxdy = ∫∫xydx =				∫xdx∫ydy .
D	0 0			0	0

Проведем двукратное интегрирование, для этого вычислим внутренний интеграл, а затем найденное решение подставим во внешний интеграл

2	y	2			2	3	2	3		y	2		2		3		x	2			3
∫ydy =						= 2 → ∫xdx∫ydy =∫x								dx = 2∫xdx = 2								=9.
										2							2
	2
0					0	0	0	0					0		0						0

6

y

2

D

0

3

x

Рис. 3

Решение (б). Построим область интегрирования (рис. 4). Выберем постоянные пределы интегрирования на оси Ox.

y

4

y = 2x

D2y = x − 4

D1

0

2

8

x

–2

у = − 2 х

Рис. 4

В этом случае область интегрирования необходимо разбить на две части D1 и D2 прямой, параллельной оси Oy, так как линия

7

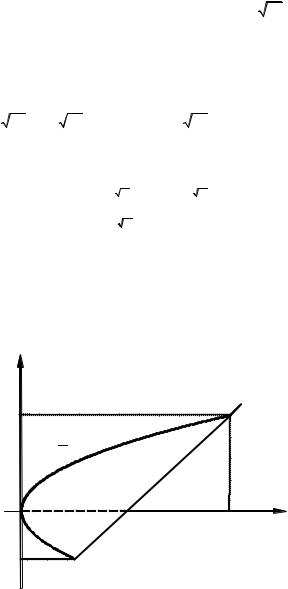
нижней границы состоит из двух частей: кривой y = − 2x и прямой y = x – 4.

Найдем абсциссы точек пересечения, приравняв уравнения линий 2x = (x– 4)2 → x1 = 2; x2 = 8.

Тогда область интегрирования D = D1 + D2,

		0 ≤ x ≤ 2,		2 ≤ x ≤8,
где D1			D2
	:	− 2x ≤ y ≤ 2x ,		:	≤ y ≤ 2x .
				x −4

Двойной интеграл в данном случае выражается двумя двукратными интегралами.

∫∫xydxdy = ∫2 xdx		∫2 x	ydy +∫8 xdx ∫2 x ydy =90 .
D	0	− 2 x	2	x −4

Заметим, что если постоянные пределы интегрирования выбрать на оси Oy, то интегрировать придется в другом порядке − сначала по x,

азатем по y.

Вэтом случае видно, что такой выбор постоянных пределов интегрирования является более удобным, поскольку разбивать область интегрирования не нужно (рис. 5).

y
4
x =	1 y 2
	2
	D	x = y + 4
0	4	8	x

–2

Рис. 5

8

Найдем ординаты точек пересечения, приравняв уравнения линий друг другу

1	y2 = y +4 → y = −2, y = 4.
2	1	2

Тогда границы области D определяются системой

−2 ≤ y ≤ 4,

D : 1 y2 ≤ x ≤ y +4 .

2

В этом случае двойной интеграл по этой области выражается одним двукратным интегралом

4 y +4

∫∫xydxdy = ∫ydy ∫ xdx.

D	−2	1	y2
		2

Вычислим внутренний интеграл

y +4				x	2			y +4			1			y	4
∫			xdx =							=		( y +4)2	−			,
1	y	2	2					1	y2	2			4
2						2

раскрыв скобки, подставим полученное выражение во внешний интеграл. Последовательное вычисление двукратных интегралов приводит к тому же результату

		1	4		3	2	y5		1 y 4				8y3	2	y 6			4
∫∫	xydxdy =		∫	y		+8y +16y −		dy =				+		+8y −					=90.
		2					4		2		4		3		24
D			−2															−2

Решение (в).

Построим чертеж области D (рис. 6, а). Поскольку область интегрирования ограничена окружностью, то удобно перейти в полярную систему координат.

Заменим в выражении x2 + y2 ≤4 знак неравенства на «равно», получим уравнение окружности (верхней границы области D) x2 + y2 = 4.

Подставив в это уравнение соотношения x = ρ cos φ, y = ρ sin φ, запишем уравнение линии в полярной системе координат

ρ2 cos2 φ + ρ2 sin2 φ = 4 → ρ = 2.

9

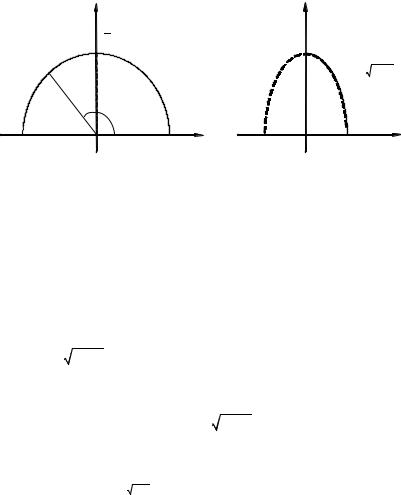
Поскольку полюс расположен на границе области D, то для «нижней» границы уравнение линии ρ = 0. Из рисунка видно, что интервал изменения угла поворота луча составляет π радиан. Таким образом, границы области D определяются системой неравенств

0		≤ ϕ≤ π,
D :	0	≤ρ≤ 2 .

а		y			б	y
			π
		2	2				2
			D				y = 2 1– x2
	ρ						D
π			φ	0
–2		0		2	x	–1 0	1	x
				Рис. 6
Двойной интеграл функции в полярной системе координат примет вид
∫ρ3 cos ϕsin ϕdρdϕ= ∫π cos ϕsin ϕdϕ∫2					ρ3dρ = 4∫π cos ϕsin ϕdϕ= 2∫π sin 2ϕdϕ= 0.
D			0	0	0		0

Решение (г). Построим чертеж области D (рис. 6, б). Выберем постоянные пределы интегрирования на оси Ox (абциссы самых крайних точек области слева и с права: x = 0, x = 1). Найдем пределы интегрирования внутреннего интеграла, для этого выразим у из уравнения эл-

липса: y = 2 1 − x2 – верхняя граница и y = 0 – нижняя граница. Тогда система, определяющая границы области

0 ≤ x ≤1,

D :

0 ≤ y ≤ 2 1 − x2 .

Проведем двукратное интегрирование – внутренний интеграл по y, затем внешний интеграл по x

		1	2 1−x2	1	1		1	1
	∫∫xydxdy = ∫xdx		∫	ydy = ∫x 2(1 − x2 )dx = −		(1 − x2 )	=		.
	D	0	0	0	2		0	2

10