помощь по matcad

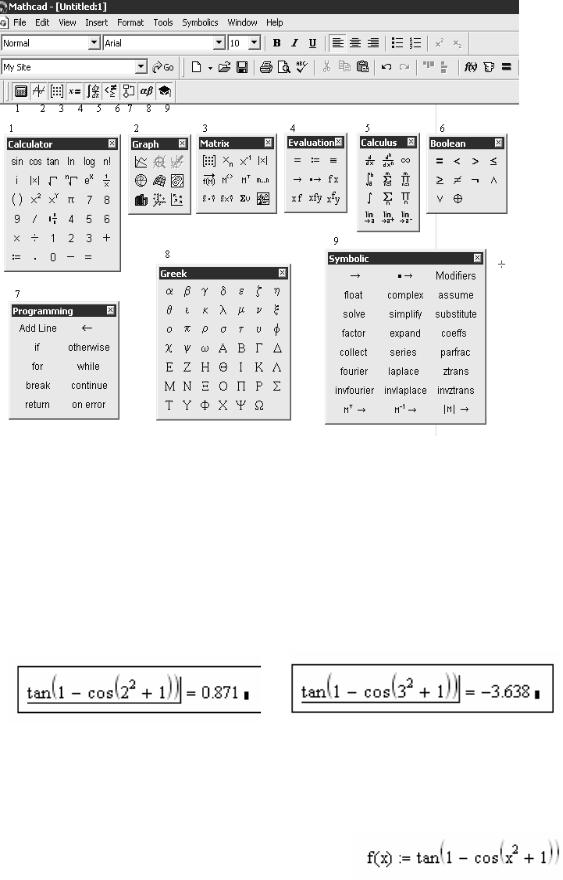
Рис.1.6. Шаблоны панели «Math»

Пример 1 . 2 . Найти значения функции f (x) = tg(1−cos(x2 +1)) при x = 2;3;10 .

Решение. Первый способ. Ввести выражение, стоящее в правой части равенства с помощью панели «Math», вместо аргумента x ввести число 2, а затем знак «=» (рис.1.7). Далее выделяем левую часть, копируем выражение,

вставляем (кнопки на панели инструментов соответственно и ), меняем 2 на 3, знак «=» – получаем результат. При x =10 аналогично.

Рис.1.7. Вычисление значений функции

Второй способ.

Описание действий	Отображение на дисплее
Функции f (x) присваиваем выражение,	стоя-

щее в правой части, с помощью знака «:=», который вводится своим первым символом «:» (двоеточие).

10

Затем вводим f (2) , знак «=» – получаем ре-

зультат.

Аналогично для любого значения x .

Задание 1 . 3 .

1.3а. Вычислить сумму N + n , где N – номер группы (только число), а n – номер по списку (например, если N =125, n =12, то N + n =137). Присвойте пе-

ременным k, m, t

значения: k – первая цифра получившегося числа ( k =1), m –

вторая цифра этого числа ( m = 3 ) и t – третья цифра числа (t = 7 ).

1.3б. Найти значения выражений:

k

x

x +1

m

1

−

+t

x +1

f (x) =

5

+ x7 при x = 5; 24 ;

x −1

x

5x

a

−

a

a

при a = 4, b = 5 .

F(a,b) =

:

a2 + ab

a +b

a +b

Во всех последующих заданиях вместо переменных k, m, t записывайте их

найденные значения.

При перемещении блоков необходимо учитывать, что Mathcad читает (и исполняет) формулы сверху вниз и слева направо. Поэтому функция, выражение должно быть определено до того, как будут произведены вычисления (то есть выше или левее).

Запомните назначение сочетания клавиш:

«Ctrl» + «.» (точка) = «→» – оператор символьного вычисления; «:» (двоеточие) = «:=» – оператор присваивания.

11

ЛАБОРАТОРНАЯ РАБОТА 2.

МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ

1. Теоретические сведения

Определение. Матрицей размера m ×n называется прямоугольная таблица, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Матрицы обозначаются заглавными буквами латинского алфавита: A, B,

C, … (или при необходимости с указанием размера, например, A ); элементы

m×n

матрицы – строчными буквами с двойной индексацией: aij , bij , …, где i – номер строки, j – номер столбца, на пересечении которых находится элемент в

матрице.

В общем случае записывают матрицы в виде:

a11

a21

A = Kai1Kam1

a	K	a	K	a
12		1 j		1n
a22	K a2 j		K a2n
K	K	K	K	K
ai2		aij
	K		K	ain
K	K	K	K
				K
am2	K amj		K amn

или сокращенно A = (aij ) , где i =1, 2,K, m ; j =1, 2,K, n .

Элементы матрицы aij , у которых номер столбца равен номеру строки

(т. е. i = j ), называются диагональными и образуют главную диагональ матри-

цы.

Две матрицы A и B одного размера называются равными, если они совпадают поэлементно, т. е. aij = bij для любых i =1, 2,K, m , j =1, 2,K, n .

		1	6			1	− 2				1
Пример 2 . 1 . A =		2	− 4						, C = (2
					, B =					−5 0), D =		.
						3	0				7
	−3		9

Матрица A имеет размер 3×2 , так как содержит 3 строки и 2 столбца, матрица B – размера 2 ×2 (квадратная матрица 2-го порядка), матрица C –

размера 1×3 (вектор-строка) и матрица D – размера 2×1 (вектор-столбец).

Виды матриц

Матрица, состоящая из одной строки (т. е. i =1), называется вектор-

строкой;

12

Матрица, состоящая из одного столбца (т. е. j =1), называется вектор-

столбцом;

Матрица произвольного размера называется нулевой или нуль-матрицей, если все ее элементы равны нулю (обозначается О).

Матрица, в которой первый ненулевой элемент каждой строки находится правее первого ненулевого элемента предыдущей строки, называется ступен-

чатой.

Матрица, у которой число строк равно числу столбцов и равно n , называ-

ется квадратной n-го порядка.

Квадратная матрица называется диагональной, если все ее недиагональные элементы равны нулю;

Диагональная матрица называется единичной, если все ее диагональные элементы равны единице (обозначается E);

Рассмотренные виды матриц можно представить в виде схемы (рис.2.1).

Произвольная матрица

Матрица –

a11

a12

K a1n

столбец

Матрица – строка

(вектор – строка i =1)

a22

(вектор –

)

a21

K a2n

A = (a

a

K a

A =

K

K

K

K

столбец

11

12

1n

m×n

j =1)

a

a

K a

b

m1

m2

mn

11

b

B =

21

K

b

m1

Нулевая матрица

Ступенчатая матрица

Квадратная матрица

0

0

K

0

a11

a12

a13

...

a1n

(m=n)

0 0 K

0

0

a

22

a

23

...

a

2n

a

a

K a

O

11

12

1n

=

K K K K

A

=

0

0

a

33

...

a

3n

A

=

a

a

K a

2n

m×n

m×n

21

22

... ...

...

... ...

n×n

K

K

K K

0

0

K

0

0

0

0

...

a

a

a

K a

mn

n1

n2

nn

Диагональная матрица

d

0

K

0

11

d22

0

D =

0

K

K

K

K K

n×n

0

0

K dnn

Единичная матрица

1

0

K 0

1

K 0

0

E =

n×n

K K K K

0

K 1

0

Рис. 2.1. Виды матриц

13

Основные операции над матрицами

1.Умножение матрицы на число. Произведением матрицы A на число

λназывается матрица того же размера B = λ A , элементы которой bij = λ aij

(для i =1, 2,K, m ; j =1, 2,K, n ), т.е. при умножении матрицы на число нужно

каждый элемент матрицы умножить на это число.
Пример 2 . 2 .	2		3	, 4A = 4	2		3	8		12
	A =							=			.
		0				0			0	−4
			−1				−1

Свойства операции умножения на число:

1.(αβ)A = α(βA).

2.(α +β)A = αA +βA .

3.0 A = O .

Следствие. Общий множитель всех элементов матриц можно выносить за знак матрицы.

12 −18 0				2		−3 0
Пример 2 . 3 .				= 6		.
	6 24	−6			1
						4 −1

2. Сложение и вычитание матриц. Суммой (разностью) двух матриц

A и B одинакового размера m ×n называется матрица C = A ± B , элементы ко-

торой cij = aij ±bij

для любых i =1, 2,K, m ;

j =1, 2,K, n (т. е. матрицы склады-

ваются и вычитаются поэлементно).

−1

−7

1

8

0

9

0

1

Пример 2 . 4 . A =

, B =

, тогда

−7

1

6

−1

1 + (−1) 8 + (−7)

0

1

1 −(−1) 8 − (−7)

2

15

0 + 0

9 +1

0 10

0 −0

9 −1

0

8

A + B =

=

; A − B =

=

.

− 7 + 6 1 + (−1)

−1 0

−13 2

− 7 −6 1 −(−1)

Свойства операции сложения матриц:

1.A + B = B + A (коммутативность).

2.(A + B)+C = A +(B +C) (ассоциативность).

3.O + A = A , где O – нулевая матрица.

3. Транспонирование матриц. Если в матрице А заменить каждую ее строку столбцом с тем же номером (или каждый столбец заменить строкой с

тем же номером), то получим матрицу AT , которая называется транспонированной к данной матрице А.

14

		1	1	0					1	3
Пример 2 . 5 .						T	=		1	−1		.
	A =					, A
		3	−1	5
									0	5

Свойства операции транспонирования:

1.(AT )T = A.

2.(A + B)T = AT + BT .

4. Умножение матриц. Умножение матрицы А на матрицу В определено тогда, когда число столбцов матрицы А равно числу строк матрицы В (в этом

случае матрица А называется согласованной с матрицей В).
Произведением матриц A B называется такая матрица	C , каждый
m×k k×n	m×n

элемент которой cij равен сумме произведений элементов i-й строки матрицы А

на соответствующие элементы	j -го столбца матрицы В:
	k
cij = ai1b1 j + ai2b2 j +K+ aik bkj = ∑ais bsj , i =1, 2,K, m ; j		=1, 2,K, n .
Вычисление элемента cij	s=1
	схематично можно изобразить так:

j

	•		•	K	•	•
i		•	•				•
				K	•
	K K			K K		K
		•	•	K			•
					•

•	•	K	•
•	•
		K	• .
K K		K K
•	•	K
			•

		1	0	2			−1		0	1
Пример 2 . 6 .						, B =		5	1	4		.
	A =
		3	1	0
								− 2	0	1
Найдем размер матрицы-произведения:									A B = C , то есть матрица C
имеет вид:									2×3	3×3 2×3
						c		c	c
						11		12	13
				C = c				c	c	.
						21		22	23

Вычислим элементы матрицы C :

c11 = a11b11 + a12b21 + a13b31 =1 (−1)+0 5 +2 (−2)= −5; c12 = a11b12 +a12b22 +a13b32 =1 0 +0 1+2 0 = 0;

c13 = a11b13 +a12 b23 +a13b33 =1 1+0 4 +2 1 = 3;

c21 = a21b11 +a22b21 +a23b31 = 3 (−1)+1 5 +0 (−2)= 2 ;

c22	= a21b12 +a22b22 +a23b32 = 3 0 +1 1+0 0 =1;
c23	= a21b13 +a22b23 +a23b33 = 3 1+1 4 +0 1 = 7 .

15

−5		0	3
Таким образом, матрица C равна: C =	2	1	7	.

В данном примере вычислить произведение матрицы В на матрицу А нельзя, т. к. количество столбцов матрицы В не совпадает с количеством строк

матрицы А: B A .

3×3 2×3

Даже если произведения матриц A B и B A существуют, то они могут быть матрицами разных размеров.

						4		−5		8					−1			5
												,	B =			−2		−3
Пример 2 . 7 . A =								3											.
						1			−1								3	4
4 −5 8				−1 5				4 (−1)+ (−5) (− 2)+8 3 4 5 + (−5)																(−3)+8 4	=
					− 2	−3
A B =								=
								1 (−1)+ 3 (− 2)+ (−1) 3 1 5 + 3(−3)+ (−1) 4
1 3	−1				3	4
30 67									−		1		5				4	−5 8					1	20 −13
							B A =			− 2			−3								=		−11 1 −13			.
=		;
	−8																1	2 −1
−10											3		4										16	−3 20

В примере 2.7 произведения A B и B A не равны между собой, кроме этого эти матрицы разных порядков. Таким образом, в общем случае произведение матриц некоммутативно, то есть:

A B ≠ B A.

При умножении квадратных матриц А и В одного порядка их произведения A B и B A существуют и имеют одинаковые размеры (того же порядка),

но, по-прежнему, в общем случае:		A B ≠ B A.
Произведение двух ненулевых матриц может равняться нулевой матрице,
т. е. из того, что A B = O , не следует, что A = O или B = O .
1	1	1	1		0	0	= O .
Пример 2 . 8 . A =	≠	O , B =		≠ O , A B =	0
1	1	−1	−1			0

Свойства операции умножения матриц:

1.A(BC) = (AB)C (ассоциативность).

2.(αA)B = A(αB) = α(AB) .

3.A(B +C) = AB + AC (дистрибутивность справа).

4.(B +C)A = BA +CA (дистрибутивность слева).

5.AE = EA = A .

6.AO = OA = O .

7.(AB)T = BT AT .

16

Замечание.

Из свойств 5 и 6 следует, что матрицы E и O перестановочны со всеми квадратными матрицами соответствующего порядка и играют на множестве матриц ту же роль, что и числа 1 и 0 – на множестве действительных чисел.

2. Вычисления с помощью системы M a t h C A D

Ввод матрицы

		Описание действий			Ввод		Отображение
1.	Для ввода матрицы на клавиатуре набираем						на экране
	имя матрицы А и знак присваивания – знак				А:=
	«:».
2.	Открываем панель операций с матрицами и
	векторами:
	меню View	Toolbars		Matrix
	кнопка .

3.В появившемся диалоговом окне ввода размеров матрицы определяем число строк (Rows), число столбцов (Columns) и закрываем окно щелчком по кнопке ОК (перемещение осуществляется с помощью курсора мыши).

3

4

4. В открывшемся справа от знака присваива-													2
ния	поле	ввода	матрицы				введите			нужные
числа. Перемещение между позициями эле-													5
													7
ментов матрицы осуществляется клавишами
													…
,	,	,	или клавишей «Tab», или
просто установкой курсора в нужной пози-													–7
ции с помощью мыши.
9 Для исправления ошибок следует использовать клавиши																	(стирает
															Delete
символ после курсора) и					← Backspace				(стирает символ до курсора).
Задание 2 . 1 . Введите элементы матриц
			−4			1	0	2				0	5	7	6
				6		4	9	−2
												3	− 4 − 2 −5
		B =		7		5	6	3			; C =
												− 4	2	0	1
				−1		3	−5	4
								17

Операции над матрицами

	Описание действий	Ввод Отображение на экране
1.	Умножение матрицы на число
	Вводим имя матрицы (матрицы А), знак
	умножения «*», который превратится в
	точку, и число (2), на которое умножаем
	матрицу.
2.	Сложение двух матриц
	Для сложения (вычитания) двух матриц
	вводим имя одной матрицы (матрицы А),
	знак «+» («-») и имя второй матрицы
	(матрицы С) и вводим знак «=».
3.	Транспонирование матрицы
	Вводим имя матрицы В, на панели «Ma-
	trix» щелкаем по кнопке	и вводим
	знак «=».
4.	Умножение матриц
	Вводим имя первой матрицы (матрицы
	А), знак «*», имя второй матрицы (мат-
	рицы В) и вводим знак «=».
5.	Возведение матрицы в степень
	Вводим имя матрицы В, знак возведения
	в степень «^», число, равное показателю
	степени, 3 и вводим знак «=».

Задание 2 . 2 . Составьте три матрицы A, B и C так, чтобы существовала матрица D = 2 A +CT − A B2 +3 C . Вычислите матрицу D .

При выборе матриц вспомните: в каких случаях возможны операции сложения, вычитания и умножения матриц?

Дополнительные возможности системы M a t h C A D при работе с матрицами

В пакете Mathcad имеются встроенные матричные функции. Для обращения к ним следует либо набрать имя функции с клавиатуры, либо выбрать нужную функцию из предлагаемого списка в разделе Vector and Matrix, открывающегося после нажатия на кнопку f (x) на панели инструментов.

18

Рис.2.2. Список функций в системе Mathcad

При описании результата применения функции будем использовать следующие матрицы:

		1	3	6			2	5	9	705
	A =	−1 − 4		7	; B =		−6	6	14	−604	; C = (1 15 66).
	0		5	5		23 7			56	25
	Функция			Описание функции							Результат
1.	Аi, j		нахождение			элемента			aij	мат-

рицы A ;

особенность этой операции состоит в том, что по умолчанию строки и столбцы в Mathcad нумеруются не с 1, а с 0, чтобы исправить это положение необходимо ввести команду ORIGIN:= 1 (она задает нумерацию

с 1);

2.indentify(n) создает единичную матрицу порядка n ;

19