математика

Пример

2	1		( 2x −1 )	4	2	1					80
∫( 2x −1 )3 dx =					=		(( 2 2	−1)4	−( 2 1 −1)4	) =		= 10
	2		4			8					8
1					1

2.Замена переменной в определенном интеграле

При подстановке dx на ϕ′(t)dt , а также учитывая, что ϕ( α) = a,

x =ϕ(t) нужно заменить х на ϕ(t) , сменить пределы интегрирования,

ϕ( β) = b :

			b					β
			∫ f (x)dx = ∫						′
									f (ϕ(t))ϕ	(t)dt .
			a					α
		Рассмотрим пример.
		Пример
				1+ x = t, 1+ x = t2
3	xdx			= x =			0 t =1;			2	(t	2	−1)2tdt		2	2
∫										= ∫					= 2∫t2 dt −2∫dt =
0	1+ x			x = 3 t = 2;						1				t	1	1
				dx = 2tdt
=	2t3		2	− 2t		2	=	2	(8 – 1) – 2(2 – 1) =				8	.
	3		1			1		3					3

При нахождении интегралов от иррациональных функций, часто необходимо сделать тригонометрическую замену.

21

	Пример
2	4x	2	x = 2 sin t	dx = 2 cos tdt
∫1		−dxx2	= x =1 t =	π	; x =	2 t =	π =
				6			4

ππ

= 4∫4	sin2 tdt = 2∫4	( 1 − cos 2t )dt = ( 2t − sin 2t )	π		π	−1 +	3 .
			π4	=
π	π		6		6		2
6	6

3.Метод интегрирования по частям в определенном интеграле

Если функции u = u( x ) и v = v( x ) имеют непрерывные производные на отрезке [a, b], то имеет место формула

b	b	b
∫udv = uv		− ∫vdu .
a	a	a

Данная формула называется формулой интегрирования по частям для определенного интеграла.

Пример

∫xe−x dx = u = x −x				du =−xdx	=
1			dv = e dx v = −e
0
		1			1
	1
= −xe−x		+ ∫e−x dx = −e−1 +0 − e−x			= −e−1 − e−1 +1 =
	0	0			0

= −2e−1 +1 .

4. Приближенное вычисление интегралов

Иногда нельзя вычислить интеграл по формуле Ньютона – Лейбница, так как подынтегральная функция может

22

быть слишком сложна или интеграл от нее будет «неберущимся». Тогда интеграл вычисляется приближенными методами. Рассмотрим самый простой из них: метод прямоугольников.

Для вычисления интеграла ∫b f (x)dx отрезок [a, b] ра-

			a
	зобьем	на n	равных частей длиной h =		b − a	:
					n
	x0 = a;	x1 = a + h;	x2 = a + 2h;...; xi	= a + ih;...; xn = b . Вы-

числим значения функции y=f(x) в точках деления и в точ-

ках x0 и xn : y0 = f (x0 ); y1 = f (x1 );...; yn = f (xn ) . Тогда имеют место такие приближенные равенства:

∫b f (x)dx ≈ h(y0 + y1 + y2 +... + yn−1 ),

a

или ∫b f (x)dx ≈ h(y1 + y2 +... + yn ).

a

Обычно вычисляют значения интеграла по обеим формулам и берут среднее арифметическое полученных значений.

Рассмотрим пример.

Пример

Интеграл ∫2 xdx вычислить точно по формуле Нью-

1

тона-Лейбница и приближенно по формуле прямоугольников. Найти абсолютную и относительную погрешности вычисления. Отрезок разбить на 10 равных частей (n=10). Промежуточные вычисления вести с тремя знаками после запятой.

23

Решение

Сначала вычислим интеграл по формуле Ньютона-

Лейбница : ∫2	xdx =	2 x1,5	2
1		3	1

=	2	( 8 −1) ≈ 1,219 .
	3

Вычислим интеграл приближенно, для этого составим таблицу значений подынтегральной функции. При этом

h=		1 −0					=0,1.
		10
	x		1			1,1					1,2	1,3					1,4	1,5	1,6	1,7	1,8	1,9	2,0
	y		1			1,049					1,095	1,14					1,183	1,125	1,265	1,304	1,342	1,378	1,414
По первой формуле прямоугольников имеем
									9									≈ 1,20 .
I1 = 0,1								∑yi = 0,1 11,981
							i=0
По второй формуле получим
I2									10									≈ 1,371.
		= 0,1 ∑yi = 0,1 13,702
							i=1
Тогда I								=		I1 + I2			=1,286 .
											2
Найдем абсолютную погрешность вычисления
	=				1,219 −1,286										= 0,067 .
Относительная погрешность будет равна
						δ =			I		100% =					0,067 100 % = 5,21% .
																1,286

Задания для контрольной работы №4

171-180. Найти неопределенные интегралы. В двух первых примерах результаты проверить дифференцированием.

171. 1) ∫ln4 xxdx ; 2) ∫xe2 x dx ; 3) ∫ x( x dx+ 4 )2 ; 24

4)

∫sin2 3xdx ;

5) ∫

2

−

3dx

.

x + 2

172.

1) ∫

tgx +1dx

; 2) ∫ln( x + 2 )dx ;

3) ∫

dx

;

cos2 x

( x − 4 )( x + 2 )2

4)

∫cos3 xdx ;

5) ∫

4

x +1

dx .

x +1 +1

173.

1) ∫

x2dx

;

2) ∫arcsin 2xdx ;

3) ∫

x + 3

dx ;

2x3 + 4

x2 + 4x + 9

4)

∫tg 2 2xdx ;

5) ∫

3

+

dx

.

x +5

174.

1) ∫

2 + 4 ln x

dx ; 2) ∫arctg2xdx ; 3) ∫cos2 4xdx ;

x

4)

∫

x2

+ 3

dx ; 5) ∫

4 − x2

dx .

( x −1)2 ( x +1)

x2

175.

1) ∫x

1 − x2 dx ;

2) ∫x sin 3xdx ;

3) ∫

x dx ;

2dx

x +1

4)

∫sin3 x cos2

xdx ;

5) ∫

x

2

.

xdx

+8x +

1

dx

176.

1)

;

2) ∫arccos 2xdx ; 3) ∫

;

1 −9x2

x( x −1)2

4)

∫sin

2

x cos

3

xdx ;

5)

∫

dx

.

(

x

+

4

x )

x

177.

1) ∫3

xdx

2 ;

2) ∫

x ln xdx ;

3) ∫cos4 2xdx ;

1 −9x

4)

∫

1 + 4x2

dx ;

∫

dx

.

x2 ( x +1)

( 1 + x2

)3

25

178.

1) ∫

xdx

;

2)

∫x ln( x +1)dx ; 3) ∫tg

3

xdx ;

(1 + x2 )3

4) ∫

x2 dx

; 5) ∫

1 + x2

x4

dx .

( x −1)( x − 2 )( x −3)

179.

1) ∫3

1arctgx+ x2

dx ;

2) x cos 2xdx ;

3) ∫3

xdx+ x ;

4) ∫

x −1

dx ;

5) ∫

cos3 xdx

sin2

x .

x2 ( x −2 )

dx

x

dx

180.

1) ∫ x 3 ln x

;

2)

∫x 5

dx ;

3)

∫

;

sin4 x

4) ∫

dx

; 5)

∫

dx

2 .

x 2x +

1

2x + 3 − x

181-190. В заданиях

вычислить интеграл

∫b

f (x)dx точно

a

по формуле Ньютона-Лейбница и приближенно по формуле прямоугольников. Отрезок [a, b] разбить на 10 частей.

Найти абсолютную и относительную погрешности вычисления. Промежуточные вычисления вести с четырьмя знаками после запятой. Приближенное значение интеграла привести с округлением до третьего десятичного знака.

	2		x2 dx								16
181.	∫							.	182.		∫4		xdx .
			( x	3	+	1)	2
	1											1
	8					1			2	1 − x2
184.	∫	x		+ 3			dx .		185. ∫				dx .
											x	4
	1					x			1
187.	4	1 + 2				x	dx .		188.	28		x −1		dx .
	∫			x	2					∫		3
	1									4

2	x4 +1
183. ∫					dx .
		x	2
1
10
186. ∫	x −1dx .
1
189. ∫1			dx				.
		(x +1)				2
	0

26

	2		2		4
190.	∫1	x		+		dx .
					x3

190-200. В заданиях вычислить интеграл ∫b															f (x)dx			по фор-
														a
муле Ньютона-Лейбница, используя метод подстановки.
	3	2 dx2			1			x2+1									1
191.	∫		+	.	192. ∫						3	dx .			193.		∫e	x dx .
	1 x	x		1	0		( x			+1)							0
	4						3										3
		dx2					∫2			dx		2 .						dx
194.	∫			.	195.				2					196.			∫		.
	2 2	x x	−	4			2 x		1 − x								1	x (x +	1)
							2
	2	dx			e					dx						81		dx
197.	∫2 x				198. ∫1											16∫
		x2 −1 .											. 199.				x( 4 x +1) .
						x( 5 − 4 ln x )2
	1 ( arctgx − 3)2
200.	∫	1 + x2			dx .
	0

27

III. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

1. Несобственный интеграл I рода

Пусть функция f ( x ) определена и непрерывна на промежутке [a;+∞). Если существует конечный предел

b

lim ∫ f ( x )dx , то его называют несобственным интегралом

b→+∞ a

+∞

первого рода и обозначают ∫ f ( x )dx . В этом случае гово-

a

рят, что несобственный интеграл сходится. Если указанный предел равен бесконечности или не существует, то интеграл

расходится.

Аналогично определяют несобственный интеграл на

b	b
промежутке (− ∞;b]: ∫ f ( x )dx = alim→−∞ ∫ f ( x )dx .
−∞	a

Несобственный интеграл с двумя бесконечными пределами определяется формулой:

+∞ ñ +∞

∫ f ( x )dx = ∫ f ( x )dx + ∫ f ( x )dx ,

−∞ −∞ ñ

где с– произвольное число. В этом случае интеграл сходится лишь тогда, когда сходятся оба интеграла справа.

Отметим,	что если непрерывная функция f ( x ) ≥ 0
	[a;+∞)	+∞
на промежутке		и интеграл ∫ f ( x )dx сходится, то

a

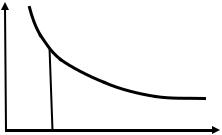
геометрически он равен площади бесконечно длинной криволинейной трапеции (рис.2).

28

y
		у=f(x)
0		x
	a
		Рис. 2

2. Несобственный интеграл II рода

Пусть функция f ( x ) определена и непрерывна на промежутке [a;b) и имеет бесконечный разрыв при x = b .

		b−ε
Если существует конечный предел	ε→lim0+0	∫ f ( x )dx , то его
		a

называют несобственным интегралом второго рода и обо-

b

значают ∫ f ( x )dx . Если предел в правой части существует,

a

то несобственный интеграл сходится. Если этот предел равен бесконечности или не существует, то интеграл расхо-

дится.

Аналогично, если функция f ( x ) терпит бесконечный разрыв в точке x = a , то полагают

b		b
∫ f ( x )dx =	ε→lim0+0	∫ f ( x )dx .
a		a+ε

29

Если функция терпит разрыв во внутренней точке с отрезка [a;b], то несобственный интеграл второго рода оп-

b c b

ределяется формулой ∫ f ( x )dx = ∫ f ( x )dx + ∫ f ( x )dx . В

a a c

этом случае интеграл называется сходящимся, если оба несобственных интеграла справа сходятся.

Примеры

Вычислить несобственные интегралы или установить их расходимость.

+∞dx

1. ∫1 x3 .

Решение

+∞dx

b

dx

1

b

1

1

=

lim

=

lim

−

= −

(0

−1)

=

∫1

x3

b→+∞ ∫1

x3

b→+∞

2x2

1

2

2

2

dx

2.

∫

.

1

x ln x

Решение

2

dx

= lim

2 d ln x

= −lim(ln

ln x

)

2

=

1 x ln x

1+ε

ln x

1+ε

∫

ε→0

∫

ε→0

= −lim(ln

ln x

)

2

= −(ln ln 2 −lim ln ln(1 +ε))= −∞ .

ε→0

1+ε

ε→0

Интеграл расходится.

30