математика

225.	Кривой y = 4(cos t + t sin t); x = 4(sin t −t cos t), ,
( 0 ≤ t ≤ 2π).		4 ).
226.	Кривой y = x3 ( 0 ≤ x ≤
		3

227.Кривой x = −ln(cos y ) , ( 0 ≤ y ≤ π3 ).

228.Кривой x =10 cos3 t , y =10 sin3 t , ( 0 ≤ t ≤ π2 ).

229.Кривой y = ln x , ( 43 ≤ x ≤ 125 ).

230.Кривой x = t − sin t , y =1 −cos t, ( 0 ≤ t ≤ 2π ).

231-240. Вычислить объем тела вращения.

231.Вокруг оси Ох фигуры, ограниченной линиями y = 2x − x2 , y = 2 − x, x = 0 .

232.Вокруг оси Оy фигуры, ограниченной линиями

y = x2 , y = x2 , y = 4, x ≥ 0 . 4

233.Вокруг оси Оy фигуры, ограниченной линиями y2 = x −1, y = 0, y =1, x = 0,5, x ≥ 0 .

234.Вокруг оси Ох фигуры, ограниченной линиями y = 2x2 , y2 = 4x .

235.Вокруг оси Оy фигуры, ограниченной линиями y2 = 4x , y ≥ 0, x =1.

236.Вокруг оси Ох фигуры, ограниченной линиями x = 4, y = x , y = 2 x .

237.Вокруг оси Ох фигуры, ограниченной линиями y = sin x, y = 3 sin x,0 ≤ x ≤ π.

238.Вокруг оси Ох фигуры, ограниченной линиями

x = 0,5, y = 0, y = 1, y = x −1 .

41

239. Вокруг оси Оy фигуры, ограниченной линиями

y= 0, y = 2x − x2 .

230.Вокруг оси Оy фигуры, ограниченной линиями x = 2, y = 0, y = x2 .

IV. КОМПЛЕКСНЫЕ ЧИСЛА. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

1. Комплексные числа

Комплексным числом называется выражение вида z = x + iy , где x, y – действительные числа; i – мнимая еди-

ница, удовлетворяющая равенству i2 = −1. Такая форма записи комплексных чисел называется алгебраической формой. Число x называется действительной частью числа

z	и обозначается Re( z ) , а число y – мнимой частью числа
z	и обозначается		Im( z ). Действительное число является
частным		случаем	комплексного числа при y = 0 . Числа
z = x + iy		и z = x −iy называются сопряженными. Два ком-

плексных числа называются равными, если равны их действительные и мнимые части.

Арифметические операции над комплексными числа-

ми:

Пусть даны два комплексных числа z1 = x1 + iy1 , z2 = x2 + iy2 .

1.Суммой ( разностью) двух комплексных чисел называется комплексное число z1 ± z2 = ( x1 ± x2 ) + i( y1 ± y2 ) .

2.Произведением комплексных чисел называется ком-

плексное число z1 z2 = ( x1 x2 − y1 y2 ) + i( x1 y2 + x2 y1 ) .

42

3. Частным двух комплексных чисел называется ком-

плексное число	z1	=	(x1 x2 + y1 y2 ) +i(x2 y1 − x1 y2 )			.
	z2
			x2	2 + y2	2

Примечание. Надо заметить, что запоминать эту формулу не стоит. При делении двух комплексных чисел достаточно домножить числитель и знаменатель на число, сопряженное знаменателю. Этот алгоритм решения продемонстрирован на примере.

Пример

Даны два комплексных числа z1 = 2 + 5i и z2 = 3 − 4i .

Найти z1 ± z2 , z1 z2 , z1 . z2

Решение

z1 + z2 = 2 + 3 + i( 5 − 4 ) = 5 + i .

z1 − z2 = ( 2 − 3 ) + i( 5 + 4 ) = −1 + 9i .

	z z		2	= ( 2 +	5i )( 3 − 4i ) = 6 +15i −8i − 20i2 = 26 + 7i .
	1
	z1		=	2 +5i	=	( 2 +5i )( 3 + 4i )	=
	z2			3 − 4i		( 3 − 4i )( 3 + 4i )

	=	6 +15i +8i + 20i2		=	−14 + 23i	= −0,56	+ 0,92i .
		9	−16i2		25
	Комплексное число				z = x + iy изображается в плоско-

сти Oxy точкой М(x, y) либо вектором, начало которого находится в точке О(0,0), а конец – в точке М(x, y) . Длина

43

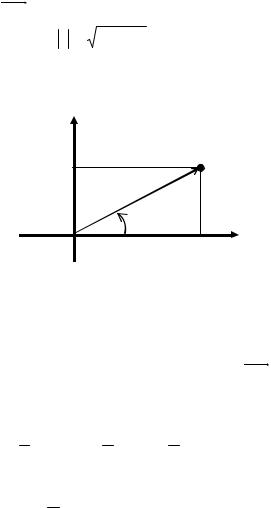
вектора ОМ называется	модулем комплексного числа и
обозначается r = z = x2	+ y2 .

Ось Ox, на которой расположены действительные числа, называется действительной осью, а ось Oy, где располагаются мнимые числа, – мнимой осью (рис. 9).

	y
	y		M(x,y)
		r
		ϕ	x
	0	x
		Рис. 9

Тригонометрическая и показательная формы комплексного числа

Угол, образованный радиус-вектором OМ с осью Ox,

называется аргументом комплексного числа и обозначается arg z . Аргумент комплексного числа ϕ находится из фор-

мул sinϕ = xr , cosϕ = ry , tgϕ = xy . Так как главное значе-

ние аргумента удовлетворяет условию −π <ϕ ≤ π , то из формулы tgϕ = xy получаем, что

44

		y
	arctg		,	x > 0,
		x
		y
	arg z = arctg		+π,	x < 0, y ≥ 0,
		x
		y
	arctg		−π,	x < 0, y < 0.
		x

Из рис. 9 очевидно, что x = r cosϕ, y = r sinϕ , откуда

комплексное число можно представить в виде

z = r(cosϕ +i sinϕ ) . Такая форма комплексного числа на-

зывается его тригонометрической формой.

Кроме того, комплексное число можно записать в по-

казательной форме z = reiϕ .

Пример

Решить данное уравнение и представить его корни в алгебраической, тригонометрической и показательной формах. Изобразить их на комплексной плоскости.

z2 − 2z + 4 = 0 .

Решение

Ищем корни квадратного уравнения

z2 + 2z + 4 = 0 ,

z1,2 =	− 2 ±	4 −16 =	− 2 ± 2	3i = 1 ± 3i .
	2		2
Имеем два комплексных числа, записанных в алгеб-
раической	форме	z1 = 1 +	3i , z2	= 1 − 3i . Запишем эти

числа в двух других формах. Для этого найдем их модули и аргументы:

45

z	1	= 1 + 3i ; z	=	1 + 3 = 2 ; arg z			1	= arctg	3 = π .
		1							1	3
		= 2(cos( π ) +i sin(			π
Тогда z1					π )) = 2e 3 i .
		3			3
Аналогично,			для		второго	числа			z2	= 1 − 3i ,
z2 =		1 + 3 = 2 , arg z2 = arctg − 3				= −		π .
					1			3
Откуда		z2 = 2(cos( −	π ) +i sin( − π )) = 2e−π3 i .
			3		3

Изобразим эти корни на рисунке (рис. 10).

y

Z1 π

3

x 0

− π

Z2 3

Рис. 10

Кроме того, приведем формулы возведения в степень комплексных чисел ( формула Муавра), а также извлечения корней из них.

zn = rn (cos nϕ + i sin nϕ ) ;

46

n z = n		r(cos ϕ + 2πk			+i sin ϕ + 2πk			),
			n				n
где k = 0,1,2,...,n −1 .
Пример
Вычислить
( i −1)	4	π i	+ 4			− 2π	+ i sin		− 2π
		+ 4e 6		3 cos		3			3	.

Ответ записать в алгебраической, тригонометрической и показательной формах.

Решение

Представим данное выражение в виде суммы трех

π

комплексных

чисел:

z1

4 = ( i −1)4 ;

z2 = 4e 6 i ;

z3 = 4

3(cos − 2π

+ i sin − 2π ) .

3

3

Преобразуем данные числа:

z1

= (−1 + i) .

z

= 1 +1 =

2 , ϕ = arctg

1

+π = −π +π =

3π

.

1

−1

4

4

Тогда z1

4 = (

2 )4 (cos

3π 4

+i sin 3π 4 ) =

4

4

= 4(cos( π) +i sin( π)) = −4 .

47

	π		π			π ) = 2 3 + 2i .
z2	= 4e 6 i = 4(cos			+ i sin
			6			6
z3	= 4 3(cos	− 2π		+i sin	− 2π ) = 4 3( −		1	−	3i ) =
		3				3	2		2

= −2 3 −6i .

z = z14 + z2 + z3 = −4 + 2 3 + 2i − 2 3 −6i = −4 −4i .

Мы нашли алгебраическую форму данного выражения. Запишем тригонометрическую и показательную формы:

z= 16 +16 = 4 2 ;

ϕ= arctg −−44 −π = π4 −π = − 34π .

Окончательно имеем

z = −4 −4i = 4 2e−	3π	i = 4 2(cos(−	3π ) +i sin(−	3π )) .
	4
			4	4

Осталось изобразить это число на комплексной плоскости (рис.11).

y

x 0

ϕ

Z

Рис. 11.

48

2.Дифференциальные уравнения первого порядка

Дифференциальным уравнением называется уравне-

ние, связывающее независимую переменную x , искомую функцию y и производные этой функции. Общий вид диф-

ференциального уравнения F(x, y, y′, y′′,..., y(n) ) = 0 . Поря-

док n старшей производной, входящей в уравнение, назы-

вается порядком дифференциального уравнения. Решением дифференциального уравнения называется функция y = f ( x ) , которая при подстановке ее в это уравнение об-

ращает его в верное тождество.

Рассмотрим уравнения первого порядка F( x, y, y′) = 0 .

Будем рассматривать уравнения, которые можно разрешить относительно производной y′, то есть записать в виде

y′ = f ( x, y ) . Общим решением уравнения первого порядка называется функция y =ϕ( x,C ) , которая удовлетворяет заданному дифференциальному уравнению при любом С, при этом найдется такое С0 , что функция y =ϕ( x,C0 ) удовлетворяет данному начальному условию y( x0 ) = y0 . Частным решением дифференциального уравнения первого порядка называется функция y =ϕ( x,C0 ) ,

которая получается из общего решения, если произвольной постоянной С придать определенное значение C = C0 . Гео-

метрически общее решение y =ϕ( x,C ) представляет собой семейство интегральных кривых на координатной плоскости. Кривая семейства, проходящая через точку M 0 ( x0 , y0 ) ,

представляет график частного решения y =ϕ( x,C0 ) . Рас-

смотрим три типа дифференциальных уравнений первого порядка.

49

2.1.Уравнения с разделяющимися переменными

Такое уравнение может быть представлено в виде dydx = f ( x )g( y ) . Для решения такого уравнения его следует

преобразовать к виду, в котором дифференциал и функция переменной x окажутся в одной части равенства, а переменной y – в другой. Затем проинтегрируем обе части полученного равенства и придем к решению уравнения.

Пример

Решить уравнение 1 + y2 = xyy′.

Решение

Представим y′ = dydx и подставим в исходной уравне-

ние 1 + y2 = xy dydx . Разделим переменные. Для этого ум-

ножим обе части уравнения на dx , разделим на х, 1 + y2 и

получим			dx	=	ydy .	Интегрируя,	получим
			x		1 + y2
∫dx	=	∫	ydy	2	, ln x =	1 + y2 + C . При этом, если инте-
x			1 + y

грал в левой части был табличным, то второй интеграл можно было вычислить отдельно:

	ydy		u =1 + y2	1 du				2		1
		=					=		u 2		+ C =
			=	1
	∫ 1 + y2		du = 2 ydy	2 ∫u				2
					2

= 1 + y2 +C .

50